Gezegenler ana yıldızlarının etrafında çok büyük mesafelerle birbirinden ayrılmış halde belli yörüngelerde dönerler. Gezegenlerin güneşlerinin yörüngesinde dönme sürelerinin birbirleriyle belirli bir ilişkisi yoktur. Ancak bazen yörüngeleri çarpıcı desenler sergileyecektir. Bu desenlerin oluşması için gezegenler arasında bir uyum, bir hizalanma meydana gelmelidir. Gezegenleri bu tür hizalanması yörünge rezonansı yardımı ile açıklanır.
Yunan matematikçi Pisagor, 2500 yıl önce demircilerin çekiçlerinin ve çalınan tellerin seslerini analiz ederek müzikal uyumun ilkelerini keşfetti. Kendisi ayrıca, matematiğin doğal dünyanın kalbinde olduğuna inanıyordu. Ek olarak Güneş, Ay ve gezegenlerin her birinin yörünge özelliklerine bağlı olarak benzersiz uğultular yaydığını da öne sürdü.
Kürelerin Müziği Ve Evreninin Uyumu
Kendisi bunu kürelerin müziği olarak isimlendirdi. Ancak bu “kürelerin müziğinin” insan kulağı tarafından algılanamayacağını düşünüyordu. Kürelerin müziğine duyulan ilgi uzun zaman varlığını korudu. Sonunda, gökbilimci Johannes Kepler, göklerdeki temel şekilleri ve melodik sesleri birbirine bağlayarak müzikal bir evren kavramını bir adım öteye taşımak istedi. Amacı, matematiksel olarak doğru ve harmonik olarak hoş olan bir dünya sistemi bulmaktı.

Bu nedenle, müzikal aralıkların ve armonilerin o dönemde bilinen altı gezegenin hareketlerini tanımladığını öne sürdü. Öncelikle gezegenlerin hareketlerini inceledi. Gezegenlerin Güneş’e göre en yavaş ve en hızlı hareket ettikleri maksimum ve minimum uzaklık noktalarındaki hızlarını hesapladı.
Sonrasında, bu iki değeri birbirine oranlayarak bazı müzikal aralıklar elde etti. ( Saturn: 5:4, Jupiter: 6:5, Mars: 3:2, Dünya 16:15 gibi). Sonrasında kitabında gezegenlerin yaydığı seslerin kulakla duyulamasa da ruhen hissedilebileceğini ve gezegenlerin düzeninin bu müzikteki uyumla ilişkili olduğunu yazdı.

Kepler’e göre güneş sisteminin iki bası vardı. Bunlar Jüpiter ve Satürn idi. Güneş sistemin de tenor Mars idi. Venüs ve Dünya iki altoydu ayrıca Merkür ise sopranoydu. Bu roller, her bir gezegenin Güneş’in etrafında dönmesi için gerekli olan süre ile ilişkiliydi. Dış yörüngedeki gezegenlerin hızları daha düşüktü, iç yörüngedeki gezegenlerin ise daha yüksekti. Bu matematiksel ilişkiler üzerine yazdığı kitaba “The Harmony of the World.” yani “Dünyanın Uyumu” adını verdi.
Yörünge Rezonansı Nedir?
Oysa ki günümüzde ses uzay boşluğunda ilerleyemediği için gezegenlerin aslında ses çıkarmadığını biliyoruz. Uzay filmlerinde çoğunlukla bunun tam tersine şahit olsak da uzayda ses duyulmaz. Çünkü uzayda ses dalgaları yayılmaz. Ses ancak içinden geçmesi gereken bir tür madde (su, hava, metal) varsa yayılır. Ancak yine de bu fikirlerin yörünge rezonansı kavramıyla bazı benzerlikleri vardır.
Yörünge rezonansı ya da yörüngesel rezonans, gezegenlerin veya ayların tam sayıların oranları olan yörünge dönemlerine sahip olması durumunda meydana gelir. Bir gezegenin yıldızının etrafında tam bir tur atması için geçen süreye periyot denir. Şimdi elimizde bir yıldızın etrafında dönen iki gezegen olsun. Ancak bir gezegenin yıldızın etrafında dönmesi diğerinin iki katı kadar zaman alsın. Bu durumda iki gezegenin periyotlarını birbirine oranlarsanız elde edeceğiniz sonuç 2:1 olacaktır.
Güneş sisteminde Neptün ve Plüton’un yörüngelerinin birbirine oranı 3:2’dir. Ayrıca Jüpiter’in üç uydusu Ganymede, Europa ve Io arasında 4:2:1 şeklinde üçlü bir uyum vardır. Bu nedenle Ganymede Jüpiter’in etrafında bir tur atarken, Europa iki kez, Io ise dört kez yörüngede döner.
Rezonanslar, gezegenlerin tam sayıların oranı olan yörünge dönemlerine sahip olması durumunda doğal olarak meydana gelir. ve yörünge rezonansları iki cismin birbiri ile etkileşim biçimini de değiştireceği için önemlidir. Bu gibi durumlarda gök cisimleri hızlanabilir, yavaşlayabilir ya da kimi durumlarda yörüngelerinde küçük sapmalar meydana gelir.
Ötegezegenlerin Yörünge Rezonansları Daha Da Karışıktır
Güneş Sistemi’nin dışındaki gezegenlere ötegezegen adı verilir. Bu gezegenleri incelemeye başladığımız zaman üç veya daha fazla nesneyi içeren rezonans örnekleri karşımıza çıkacaktır. Örneğin Gliese 876 yıldızı, Jüpiter’in üç uydusu gibi, yörüngelerinin birbirine oranı 4:2:1 olan üç gezegene sahiptir. Kepler-223 yıldız sistemi ise, yıldızın etrafında dönen 4 gezegenden oluşur. Bu gezegenlerin yörüngelerinin oranı 8:6:4:3 biçimindedir.
Ancak bu konuda Trappist-1 bir rekora sahiptir. Trappist-1 yıldızının yörüngesinde Dünya büyüklüğünde yedi gezegenden oluşur ve bunlardan ikisinin yaşanabilir olduğu düşünülmektedir. Bu gezegenlerin yörüngelerinin birbirine göre oranları da 24:15:9:6:4:3:2 biçimindedir.
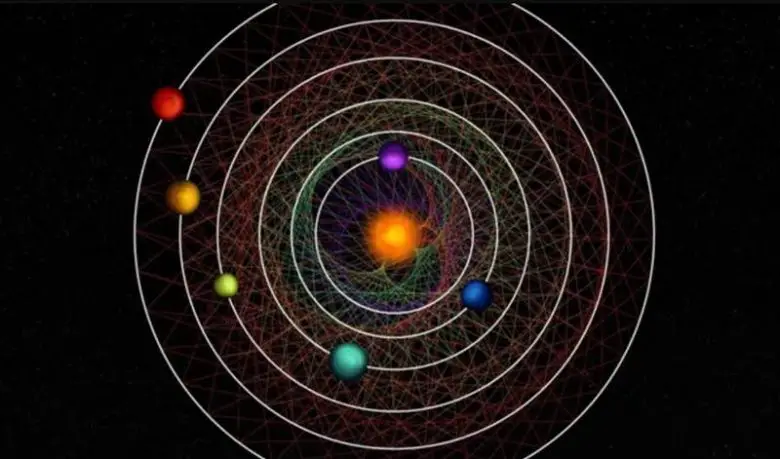
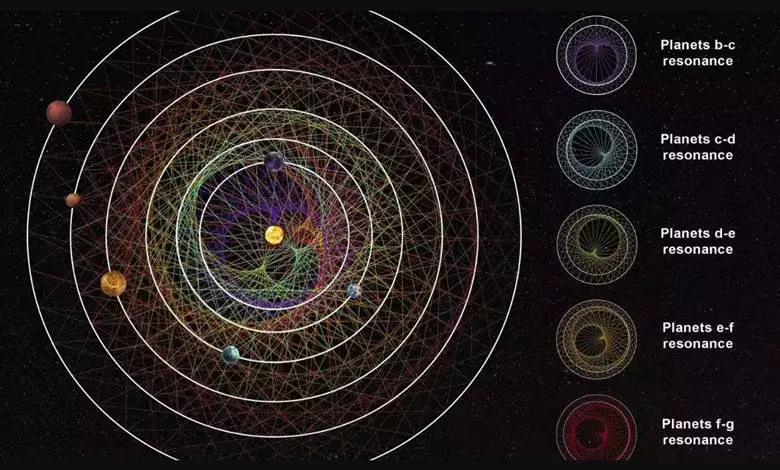
Rezonans zincirinin en yeni örneği ise HD 110067 sistemidir. HD 110067 için matematiksel olarak mükemmel bir ötegezegen sistemi diyebiliriz. Yaklaşık 100 ışıkyılı uzaklıkta bulunan bu sistemde 54:36:24:16:12:9 yörünge oranlarıyla 6 gezegen bulunmaktadır. Ancak bu sistemin ilginçliği sadece bu değildir.
Normalde rezonans zincirleri kararsızdır ve zamanla kaybolur. Ayrıca verdiğimiz örneklere rağmen, bu tip tamsayı oranları nadirdir ve tüm gezegen sistemlerinin yalnızca %1’inde görülür. Ancak HD 110067 farklıdır. Bu 6 gezegenin milyarlarca yıl boyunca aynı oranda hareket ettiği anlaşılmıştır.
Kürelerin Müziğini Bu Sefer Dinleyebilir miyiz?
Gökbilimciler, karmaşık görsel verileri sese dönüştürmek için sonifikasyon adı verilen bir teknik kullanır. Bu teknik sayesinde de, gezegenlerin matematiksel ilişkilerini de sese dönüştürmemiz mümkündür. Gökbilimciler TOI 178 ötegezegen sistemi için bunu yapmayı denediler. Sonucu aşağıda dinleyebilirsiniz.
Gökbilimciler ayrıca HD 110067 sistemi için de benzer bir çalışma yaptılar. İlk dinlediğiniz zaman büyük bir ihtimal ile kulağa gerçek bir müzik gibi gelmeyecektir. Ancak Pisagor’un fikirlerinin 2.500 yıl aradan sonra bir biçimde hayata geçtiğini görmek yine de ilham vericidir.
Kaynaklar ve ileri okumalar
- Orbital resonance − the striking gravitational dance done by planets with aligning orbits. Yayınlanma tarihi: Kaynak site: Conversation. Bağlantı: Orbital resonance − the striking gravitational dance done by planets with aligning orbits
- Malhotra R. New results on orbital resonances. Proc Int Astron Union. 2021 Oct;15(Suppl 364):85-101. doi: 10.1017/s1743921321001411. Epub 2022 May 30. PMID: 35651635; PMCID: PMC9153285.
- Luque, R., Osborn, H.P., Leleu, A. et al. A resonant sextuplet of sub-Neptunes transiting the bright star HD 110067. Nature 623, 932–937 (2023). https://doi.org/10.1038/s41586-023-06692-3
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel