İster bir tartışmayı çözmek, ister bir futbol maçında ilk başlama vuruşunu kimin yapacağına karar vermek olsun, yazı tura atma yöntemi, belirsizlikleri çözmek için yüzyıllardır kullanılan popüler bir araçtır. Yazı tura, birçok kişi için rastgelelik ve tarafsızlık ile eşanlamlı hale gelmiştir. Ancak, bu yöntem her zaman göründüğü kadar adil değildir.

Madeni para atışı, tarafsızlık ve rastgelelik kavramlarını simgeler. İnsanlar, tartışmaları çözmek, karar almak veya şansa dayalı bir sonuç üretmek için bu yöntemi kullanır. Sürecin basitliğini ve yazı ya da tura gelme ihtimalinin eşitliğini adaletin temeli olarak görürler.
Ancak araştırmalar, bu yöntemin aslında beklenenden daha karmaşık olduğunu ortaya koyar. Madeni paranın tasarımı, fırlatma tekniği ve çevresel faktörler, sonucu doğrudan etkiler. Paranın ağırlık dağılımındaki dengesizlikler, fırlatmada kullanılan güç ve dönme hareketi, yazı tura atışını tarafsızlıktan uzaklaştırır. Bu durum, yazı tura atışının adil olduğu algısını temelden sarsar.
50-50 Şans Yanılsaması
İlk bakışta, madeni para atışı, yazı ve tura için eşit şans sunduğu izlenimini yaratır. İnsanlar, paranın simetrik olduğunu ve dış kuvvetlerin her iki yüzüne eşit şekilde etki ettiğini varsayar. Ancak madeni paralar, genellikle fark edilmeyen küçük tasarım kusurları taşır.
Şekillerindeki asimetriler, kütle dağılımındaki dengesizlikler ve yüzey dokularındaki farklılıklar, atış sonucunu doğrudan etkiler. Örneğin, baş tarafı daha ağır olan bir para, ağırlık merkezinin etkisiyle tura gelme eğilimindedir. Bu küçük kusurlar, birden fazla atış yapıldığında etkisini artırır ve sürecin tarafsızlığını ortadan kaldırır.

Madeni para atışının fiziği de, sonucun belirlenmesinde kritik bir rol oynar. Havaya bir madeni para fırlatmak, tahmin edilenden daha karmaşık fiziksel süreçleri içerir. Paranın başlangıç pozisyonu, fırlatma sırasında uygulanan açısal ve doğrusal ivme, yere düştüğü yükseklik, hatta uçuş sırasında maruz kaldığı hava direnci gibi faktörler sonucu etkiler.
Tüm bu unsurları yeterince hassas ölçebilirseniz, madeni paranın hangi yüzünün geleceğini kesin olarak tahmin edebilirsiniz. Bu da aslında yazı tura atışının rastgele olmadığını açıkça gösterir.
Persi Diaconis ve Yazı Tura Atışı
Stanford Üniversitesi’nden matematikçi ve istatistikçi Persi Diaconis, yazı tura atışının rastgele olmadığını kanıtlamak için kapsamlı araştırmalar yürütmüştür. Diaconis’in çalışmaları, parayı atan kişinin hareketlerinin genellikle paranın başlangıç pozisyonunu koruduğunu ortaya koymuştur.

Diaconis, parayı atan kişinin hareketlerinin çoğunlukla madeni paranın başlangıç pozisyonunu koruyacak şekilde bir eğilim gösterdiğini ortaya koydu. Eğer madeni para baş yukarı pozisyonda fırlatılmışsa, baş gelme olasılığı %51’e yükseliyordu. Yakın zamanda yapılan bir araştırma da onun haklı olduğunu kanıtladı. Ancak bu küçük önyargının kanıtlanması, yüzbinlerce titizlikle kaydedilen yazı-tura atmayı gerektirecekti.

Yazı Tura Atışında Olasılık Neden Eşit Değil?
Attığımız yüzün gelme olasılığının neden daha fazla olduğunu anlamak için gündelik hayattan basit bir gözlemi hatırlayabiliriz. Örneğin, el yapımı pizza yapan bir restorana gittiğinizde, ustaların pizza hamurunu havaya fırlattığını ve aynı zamanda çevirdiğini görmüşsünüzdür. Bu hareketin amacı, hamurun havada düzgün bir şekilde dönmesini sağlarken ters yüz olmasını engellemektir. Yani, hamur başlangıçta hangi yüzü yukarı bakıyorsa, fırlatma sonrasında da aynı yüz yukarıda kalır.

Bu basit gözlem, bir madeni para atışının dinamiklerini anlamamıza da ışık tutabilir. İnsanların madeni parayı fırlatırken uyguladığı dönme hareketi genellikle benzer bir etki yaratır.
Paranın açısal momentumu, başlangıç pozisyonunun korunmasına neden olur ve bu da fırlatma sırasında yukarı bakan yüzün, yere düştüğünde yine yukarı gelme olasılığını artırır. Pizza ustalarının hareketiyle yazı tura atışının benzer fiziksel prensiplere dayanıyor olması, günlük hayattaki alışkanlıkların bilimsel süreçlere nasıl ışık tutabileceğini gösterir.
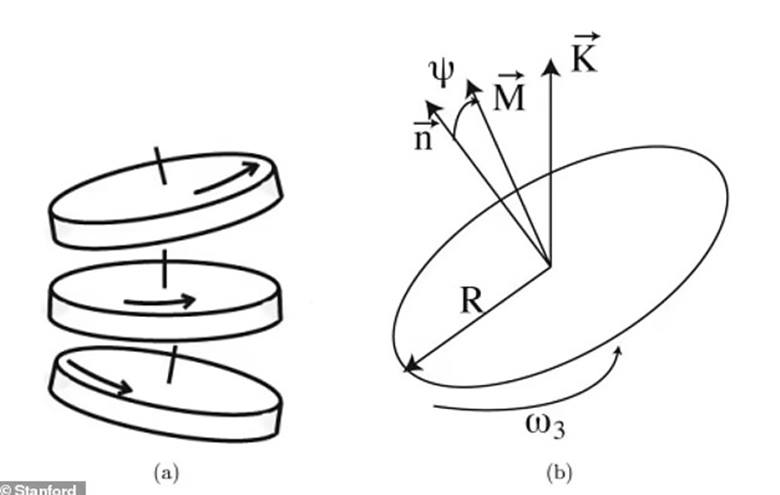
Yukarıdaki görselde de gördüğünüz gibi, bir bozuk parayı havaya fırlattığınızda, paranın hafifçe yalpalamasına ve dönmesine neden olursunuz. Bu hareket, paranın atış anında yukarı bakan tarafının yere düştüğünde de yukarı gelme olasılığını artırır.
Eğer gerçekten adil bir yazı tura atışı yapmak istiyorsanız, parayı havaya attıktan sonra yakalamayı deneyebilirsiniz. Zemin kadar düz olmayan el yüzeyi, paranın geometrisinden kaynaklanan dengesizlikleri bir ölçüde telafi eder. Ancak bu yöntem de tamamen tarafsız değildir. Başlangıç pozisyonu, yakalanan yüzü belirlemede yine etkili olur ve %51 oranındaki eğilim devam eder.
Sonuç Olarak
Sonuç olarak, yazı tura atışı sanıldığı kadar adil ya da rastgele değildir. Paranın tasarımındaki küçük kusurlar, fırlatma sırasında kullanılan teknikler ve çevresel faktörler, sonucun büyük ölçüde rastgele olmamasına neden olur. Tek bir atışta bu etkiler fark edilmese de, yeterince fazla sayıda atış yapıldığında belirgin bir eğilim ortaya çıkar.
Bu bilgiyi yazı tura oyununda bir avantaj olarak kullanabilirsiniz. Eğer parayı atan sizseniz, başlangıçta yukarı bakan yüzü dikkatlice seçin. Eğer kazanmak istiyorsanız, attığınız paranın üst yüzeyini rakibinize göstermeyin. Böylece olasılıklar küçük bir farkla da olsa sizin lehinize işleyecektir.
Kaynaklar ve ileri okumalar
- Diaconis, Persi & Holmes, Susan & Montgomery, Richard. (2007). Dynamical Bias in the Coin Toss. Siam Review – SIAM REV. 49. 211-235. 10.1137/S0036144504446436.
- Heads or tails? Coin tosses are NOT 50/50, scientists say. Here’s how to boost your chance of choosing the right side. Yayınlanma tarihi: 11 Ekim 2023. Bağlantı: Heads or tails? Coin tosses are NOT 50/50, scientists say. Here’s how to boost your chance of choosing the right side
- František Bartoš et al. Fair coins tend to land on the same side they started. Evidence from 350,757 Flips, arXiv (2023). DOI: 10.48550/arxiv.2310.04153
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel








