Yağmurda Daha Az Islanmak İçin Yürüyelim mi? Koşalım mı?

Şemsiyesiz sokağa çıktığınız bir zamanda sağanak yağmura yakalandığınızı varsayalım. En az ıslanmak için ne yapmalısınız? Elbette bir yerlere oturup yağmurun geçmesini bekleyebilirsiniz. Ancak bir randevunuz varsa hareketsiz durmak iyi bir seçenek olmayabilir. Bu durumda diğer iki gerçekçi seçeneğiniz gitmeniz gereken yere yürümek veya yağmurda koşmak olacaktır.

Yürürseniz, daha uzun süre yağmurda kalacağınız için daha çok ıslanacaksınız. Koşarsanız, koşarken daha fazla yağmur damlasıyla çarpışacağınız için daha çok ıslanacaksınız. Tercihiniz hangisinden yana olmalıdır? İçgüdülerimiz koşmanın ıslanmamızı en aza indireceğini söyler. Peki bu gerçekten doğru mu?

Bu yaygın ikileme bilimsel bir bakış atalım. Ancak şu anda yağmur altında bir yerlerde saklanmış ve bu yazıyı okumaya çalışıyorsanız baştan söyleyelim. Mümkün oldukça hızlı koşun…

Yağmur yağdığında neden koşmalısınız?

Yağmura yakalandığınız sırada elinizde bir sünger bulundurduğunuzu hayal edin. Varacağınız yere yürüyerek 15 dakikada gittiğinizi kabul edelim. Bu durumda elinizdeki süngeriniz 15 dakika boyunca yağmur suyunu emecektir. Ancak koşmanız durumunda varacağınız yere 10 dakikada varabilirsiniz. Bu nedenle de süngeriniz sadece 10 dakika yağmurla yüzleşir.

Ancak bu deneyle ilgili bir sorun var. Süngerimiz ile ilgili düşünce deneyimizi yalnızca dikey yönde düşen yağmuru dikkate alarak yaptık. Ancak yağmur sadece tepemizden değil koşma durumumuzda önden de bize çarpacaktır.

 Peki yağmurda ıslanma sürecini azaltmak için yapılacak en iyi şey nedir? Size ilginç gelebilir ancak bu soru aslında son birkaç on yılda matematik dergilerinden Mythbusters gibi TV şovlarına kadar çokça tartışıldı (aslında bu konuda iki bölüm yaptılar, ikincisi düzeltmeydi!). Sonucunda da cevap koşma olarak çıktı. Bunun nedenini anlamak için basit bir model üzerinden ilerleyelim.

Matematiksel olarak yağmurda koşmak neden daha iyidir?

Aşağıdaki şekildeki sağa doğru V hızıyla hareket eden dikdörtgen süngerimizi bir kere daha inceleyelim. Yağmur damlaları u hızıyla düşsün. Süngerin üst yüzey alanı A_t, ön yüzeyinin alanı ise A_f‘dir. Havada m³ başına düşen yağmur damlası sayısını da ‘n’ sabiti ile gösterelim.

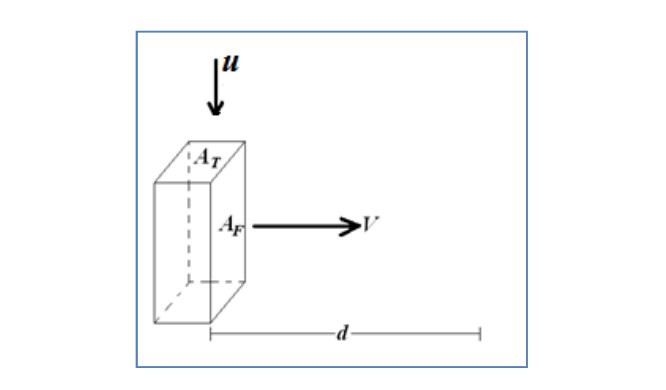
Yağmur damlalarının süngerin üst kısmından emilme hızı (saniyedeki damla sayısı) R_tepe =n.u.A_t biçiminde olacaktır. Sonucumuzun süngerin hızından bağımsız olduğuna dikkat edelim. Benzer bir biçimde yağmur damlalarının süngerin ön kısmı tarafından emilme oranı da R_{ön yüz}= n. V. A_f biçiminde olur.

İkinci denklemde süngerin ön tarafından emilim oranı süngerin hızına bağlıdır ve hız arttıkça bu oran artar. Çok hızlı düşünürseniz, yavaş yürümenin faydalı olduğu sonucuna varacaksınız. Sonucunda bu durumda emilim oranı daha az olacak ve daha kuru kalacaksınız.

Ancak sığınağa ulaştığınızda ne kadar ıslanacağınız konusunda hızın gerçekten bir fark yaratıp yaratmadığını görmek için, sığınağa varıncaya kadar geçen sürede süngere kaç damlanın gireceğini de bulmamız gerekir. Bu nedenle hesaplamaya değişkenimiz ‘t’ yani zamanı eklemeliyiz. Hatırlatalım: t = Yol / hız = d/V biçimindedir.

Dolayısıyla, ‘t’ zamanında kişinin maruz kalacağı toplam yağmur miktarına N dersek, N = (R_tepe + R_ön) x t biçiminde düşünebiliriz. Yukarıdaki denklemlerde elde ettiğimiz sonuçları yerlerine yazarsak ve gerekli sadeleştirmeleri yaparsak N = [(n.u A_t .d) / V] + (n.A_f .d) sonucunu elde ederiz.

Yukarıdaki denklem bize iki sonuç veriyor. Süngerin ön kısmına giren toplam damla sayısı süngerin hızına hiç bağlı değildir! ( Sadeleşme sonucunda V’ler birbirini götürür). Süngerin üst kısmına giren damlaların toplam sayısı, süngerin üst kısmına giren damla sayısı ile ters orantılıdır. ( V’nin paydada olduğuna dikkat edin). Yani sünger ne kadar yavaş hareket ederse süngerin üst kısmına o kadar fazla damla girer. Bu durumda hızı arttırmak yani yağmurda koşmak, yağmur damlası sayısını azaltacak ve dolayısıyla daha az ıslanmamızı sağlayacaktır.

Ya Yağmur Çapraz Yağarsa?

Eğer yağmur W rüzgar hızı nedeniyle belli bir açıyla yağıyorsa, o zaman damlaların süngerin ön kısmından emilme hızını hesaplamak için sadece V kullanmak yerine, damlaların rüzgar hızına göre hızını kullanmalıyız. Bu durumda son hızımız V_r = V – W kadar olacaktır. ( W yani rüzgar hızının karşıdan geldiğini varsayıyoruz.)

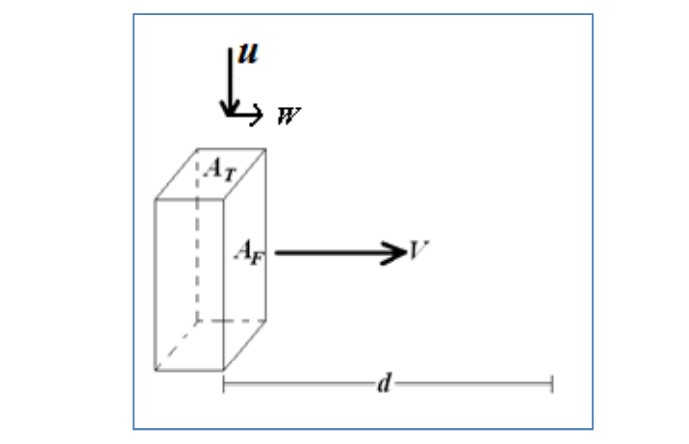
Karşıdan yağan bir yağmur olduğunda süngerin ön yüzünün daha fazla ıslanacağı açıktır. Bunu da R_{ön yüz}= n. (V- W). A_f yardımı ile ispatlayabiliriz. Yukarıdaki hesaplamalardaki adımları tekrarlarsak N = [(n. u. A_t .d) / V] + [n. A_f .d.(V-W) / V] sonucunu elde ediyoruz. ( Bu sefer V’lerin sadeleşmediğine dikkat edin).

Sonucunda rüzgar hızıyla (V = W) hareket ederseniz bu denklemin ikinci bölümü kaybolur ve tek su akışı süngerin tepesinden olur. O kadar hızlı koşamasanız bile bu katsayının küçük olması daha az ıslanmanız anlamına gelecektir.

Sonuç olarak

Sonucunda yağmurda daha az ıslanmak istiyorsanız, öne eğilip, mümkün oldukça hızlı koşun. Ancak gerçekten daha kuru kalmak için, bunu telafi edecek kadar hızınızı artırmanız gerekir. Ya da yağmurda koşmak yerine yanınızda bir şemsiye taşıyın!

Kaynaklar ve ileri okumalar:

• Is It Better to Walk or Run in The Rain? Yayınlanma tarihi: 9 Şubat 2015. Kaynak site: Sciencealert. Bağlantı: Is It Better to Walk or Run in The Rain?
• Bocci, Franco. (2012). Whether or not to run in the rain. European Journal of Physics. 33. 1321. 10.1088/0143-0807/33/5/1321.
• Walk or run in the rain? A physics-based approached to staying dry (or at least getting less wet). Yayınlanma tarihi: 20 Ekim 2024. Kaynak site: Conversation. Bağlantı: Walk or run in the rain? A physics-based approached to staying dry (or at least getting less wet)

Size Bir Mesajımız Var!

Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak, bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca, yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.

Matematiksel