Bir matematikçi değilseniz Voronoi diyagramları adını ilk defa duyuyor olmanız olasıdır. Ancak farkında olmasınız da hemen her gün bu şekiller ile yüzleşirsiniz.

Zürafanın kürküne yakından baktığınızda, birbirine yapboz parçaları gibi oturan düzensiz kahverengi lekeler görürsünüz. Yusufçuk kanatlarındaki ince damarlar da aynı biçimde, düzensiz ve saydam hücrelerden oluşan bir ağ oluşturur.
Doğada görülen bu farklı desenlerin tümü, matematikte Voronoi döşemesi (ya da Voronoi tessellation) adı verilen bir yöntemle modellenir.

Voronoi Diyagramları Nedir?
Adını Rus matematikçi Gregory Voronoi’den (1868- 1908) alan Voronoi diyagramı, düzleme rastgele yerleştirilmiş noktalardan oluşan bir diyagram türüdür. Bu diyagramda, her bir nokta çevresinde kendisine en yakın bölgeyi tanımlar ve düzlemi hücrelere ayırır. Bu hücreler, düzlemi boşluk bırakmadan kaplayan çokgenleri oluşturur ve birlikte bir döşeme meydana getirir.
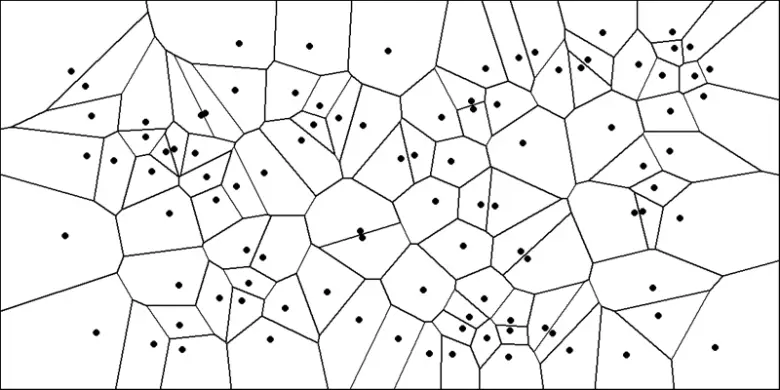
Örnek olarak, aşağıdaki şekilde 100 rastgele nokta ve bu noktalara karşılık gelen Voronoi diyagramı yer alıyor. Her nokta, kendi etrafında bir hücreyle çevrilidir. Bu hücrenin sınırları, iki ya da daha fazla nokta arasında eşit uzaklıkta olacak biçimde oluşur. Başka bir deyişle, her hücrede yer alan tüm noktalar, o hücredeki merkeze diğer tüm noktalardan daha yakındır.
Voronoi diyagramlarının oluşturduğu desen, doğada oldukça yaygındır. Bu yaygınlığın ilk nedeni, Voronoi desenlerinin son derece verimli şekiller oluşturmasıdır. Daha önce belirtildiği gibi, Voronoi diyagramı düzlemi tamamen döşer; böylece hiçbir alan boşa gitmez. Bu özellik, sınırlı bir hacimde maksimum alan kullanımı gerektiren yapılarda büyük bir avantaj sağlar.
Bir Voronoi diyagramındaki her noktayı, komşu hücrelerdeki noktalarla birleştirirseniz, Delaunay üçgenlemesi adı verilen bir ağ yapısı elde edersiniz. Aşağıdaki şekilde, siyah çizgiler Voronoi diyagramını, gri çizgiler ise Delaunay üçgenlemesini gösterir. Bu iki sistem, aynı geometrik bilgiyi farklı biçimlerde sunar. Biri alanı hücrelerle bölerken diğeri bu hücreleri üçgenlerle birbirine bağlar.
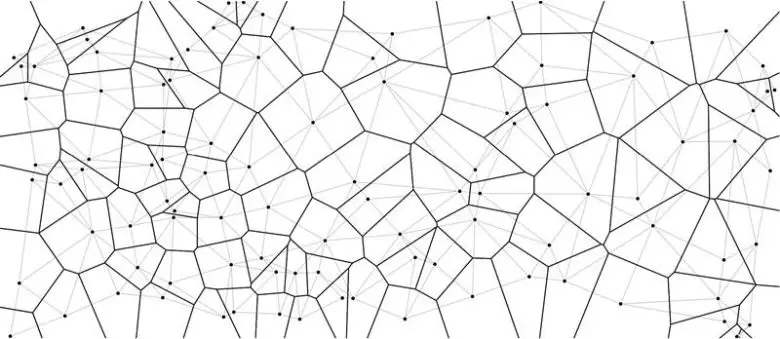
Delaunay üçgenlemesi, Voronoi diyagramları kadar etkileyici bir yapıdır. Adından da anlaşılacağı gibi, bu yöntem noktaları birbirine bağlayarak bir dizi üçgen oluşturur. Bu üçgenlerin özelliği, her birinin köşelerinden geçen bir çember çizildiğinde, bu çemberin içinde başka hiçbir noktanın bulunmamasıdır.
Bu özellik, Delaunay üçgenlemesini nokta kümelerinden yüzeyler ve nesneler oluşturmak için etkili bir yöntem hâline getirir. Bu teknik, ağ yapıları üretmekte, bilgisayar animasyonlarında üç boyutlu modeller oluşturmakta ve CBS (Coğrafi Bilgi Sistemleri) çalışmalarında arazi yüzeylerini modellemekte yaygın olarak kullanılmaktadır.
Kolera Salgını ve John Snow’un Haritalandırma Çalışması
Voronoi diyagramları, mekânsal ilişkileri incelemede yaygın biçimde kullanılmaktadır. Kullanım alanlarına dair ilginç bir örnek tıp tarihi ile alakalıdır.

On dokuzuncu yüzyıl Londra’sı kalabalık, kirli ve kötü kokuluydu. Bu ortam insanlar için yaşanmaz, mikroplar içinse adeta bir cennetti. 1831’de kolera İngiltere’ye ulaştı ve on binlerce insan bu hastalığa yenik düştü.
Dönemin hekimleri, diğer bulaşıcı hastalıklarda olduğu gibi, kolerayı da “miasma” adı verilen kötü havaya bağladı. Onlara göre insanlar hastalığı, “kolera sisi” olarak adlandırılan zehirli havayı soluyarak kapıyordu. Ancak doktor John Snow’un başka bir fikri vardı.
Belediye kayıtlarını dikkatle incelediğinde, Londra’daki farklı su şirketlerinden su alan bölgelerde koleradan ölüm oranlarının büyük farklılıklar gösterdiğini fark etti. Southwark & Vauxhall (S&V) ile Lambeth su şirketleri aynı kaynaktan, yani Thames Nehri’nden su taşıyordu. Buna rağmen, S&V’nin hizmet verdiği bölgelerde her on bin kişiden 315’i koleradan ölürken, Lambeth’in su sağladığı bölgelerde bu sayı yalnızca 37 idi.
Thames, o dönemde Londralılar için yalnızca içme suyu kaynağı değil, aynı zamanda kanalizasyonun da döküldüğü son noktaydı. Snow’un ifadesiyle S&V, bu “son derece kirli” suyu hiçbir işlemden geçirmeden yeniden müşterilerine ulaştırıyordu. Lambeth ise kısa süre önce tesislerini, kanalizasyonun döküldüğü bölgenin ötesine taşımıştı. Bu bulgu, hastalığın kirli suyla yayıldığını güçlü biçimde düşündürüyordu.

Snow, salgındaki ölümlerin coğrafi dağılımını çarpıcı biçimde ortaya koyan son derece yaratıcı bir harita hazırladı. Veriler, ölümlerin Soho’daki Broad Street’te bulunan su pompasının çevresinde kümelendiğini ortaya koyuyordu.
Snow’un bir sonraki adımı, haritadaki her evi en yakın su pompasına göre sınıflandırarak bölgeyi belirgin alanlara ayırmak oldu. Bugün bu tür düzlem bölünmelerine, Voronoi diyagramı diyoruz.
Sonuç Olarak
Bir Voronoi diyagramı oluşturmak için düzlem üzerinde belirli noktalar tanımlarız; örneğin, Golden Square haritasındaki su pompaları. Ardından düzlemdeki diğer noktaları —örneğin kolera kurbanlarının evlerini— ele alır ve her biri için bu önceden tanımlanmış noktalardan en yakında olanı belirleriz.
Böylece düzlem, her biri yalnızca bir referans noktası içeren bölgelere ayrılır. Her bölge, içindeki noktaların en yakın olduğu merkezi noktayı temsil eder. Snow’un haritasında her bölge bir su pompasını ve o pompaya en yakın evleri kapsıyordu.
Snow, o dönemde adı konmamış bu yöntemi kullanarak salgının kaynağını belirlemeyi başardı. Snow’un Soho’daki kolera salgınına ilişkin bu güçlü matematiksel analizi, hastalığın su yoluyla bulaştığına dair teorisini sonunda yetkililere kabul ettirdi. Broad Street pompasının kolu kaldırıldı ve salgın kısa sürede sona erdi.
Snow’un su kaynaklı bulaşmayı matematiksel kanıtlarla göstermesi, modern epidemiyolojinin ve hastalıkları anlamada matematiğin kullanılmasının başlangıç noktalarından biri oldu.
Kaynaklar ve ileri okumalar
- Maths in a minute: Voronoi diagrams; Yayınlanma tarihi: 30 Mart 2020. Kaynak site: Plus maths. Bağlantı: Maths in a minute: Voronoi diagrams/
- Gómez-Gálvez, P., Vicente-Munuera, P., Tagua, A. et al. Scutoids are a geometrical solution to three-dimensional packing of epithelia. Nat Commun 9, 2960 (2018). https://doi.org/10.1038/s41467-018-05376-1
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel