Çocukluğunuz da muhtemelen tic-tac-toe oyununu en az bir kez oynamışsınızdır. Bu oyun yakın zamanda ülkemizde de üç taş oyunu olarak tanınmaya başladı. Bildiğiniz gibi bu oyunun kuralları son derece basittir. Ancak eğer matematiğe ilgi duyan biri iseniz, bu oyun sizi tahmininizden çok daha fazla oyalayacaktır.

Tic-tac-toe iki oyunculu bir oyundur ve her iki oyuncu tarafından da en iyi şekilde oynanırsa her zaman beraberlik ile sonuçlanır. Bu oyun geleneksel anlamda bir kağıda çizilerek ya da sınıf ortamında bir tahtaya çizilerek oynanır. Yapmanız gereken X ve O harflerini belli bir stratejiye göre 3 x 3’lük bir ızgaraya yerleştirmektir. Aynı oyunu farklı renkte pullar ya da taşlar ile de oynamanız mümkündür. Zaten üç taş oyunu ile Tic-tac-toe arasındaki tek fark budur.
Arkeolojik bulgular bu oyunun MÖ 1. yüzyıl civarında Roma İmparatorluğu’nda da oynandığını bizlere gösteriyor. O dönemde adına “Bir seferde üç çakıl taşı” anlamına gelen “terni lapilli” dendiğini biliyoruz. Oyunun ızgara işaretlerine, bir çok Roma kalıntısında rastlanıyor. Ayrıca antik Mısır döneminde de bu oyunun bir benzerinin oynandığı düşünülmektedir.

Üç Taş Oyunu Nasıl Oynanır?
Çoğumuz bu oyunu bir çocuk oyunu olarak düşünsek de aslında oyun ızgarasını büyütürsek bu oyun giderek daha karmaşık hale gelecektir. Standart bir oyunda amacınız üç tane X ya da üç tane O harfini bir satırda, sütunda ya da köşegen üzerinde sıraya dizmektir. Sonucunda berabere kalınan tipik bir oyun aşağıdaki gibi gözükecektir. Oyuna ilk kimin başlayacağına dair evrensel olarak kabul edilmiş bir kural yoktur. Ancak genellikle X harfini seçen kişi ilk başlamaktadır.
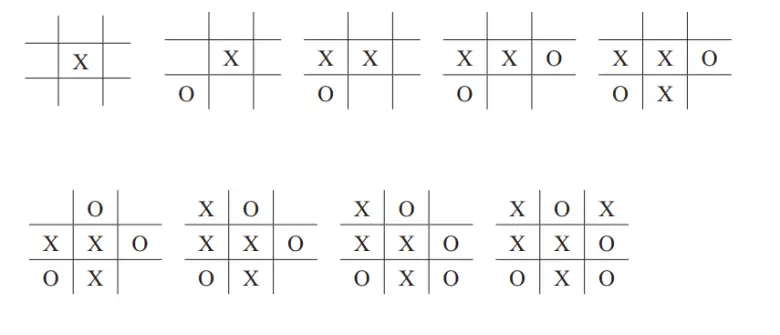
Üç taş oyunu, tahtanın boyutunu 4’e 4, 5’e 5 veya hatta 20’ye 20 ızgaraya yükselterek önemli ölçüde daha karmaşık hale getirilebilir. Kazanmak için kesin bir kural yoktur. Daha önce de dediğimiz gibi iyi oynayan iki oyuncu hemen her zaman oyunu berabere bitirecektir. Ancak ilk hamleyi yapan kişinin ilk etapta merkezi ya da köşeleri tercih etmesi önerilmektedir.
Bir yandan kazanmak için hamle yaparken öte yandan rakibin kazanmasının engellenmesi gerektiği de unutulmamalıdır. Bu süreçte en iyi strateji rakibinizin yaptığı hamlenin tam zıttını yapmak olacaktır. Yani, rakip sağ üst köşeyi seçtiyse, siz sol alt köşeyi; en üst ortayı i seçtiyse siz de en alt ortay seçin ve bu biçimde devam edin. Ancak hatırlatalım. Bu taktik 3 x 3, daha genel olarak n bir tek sayı olmak koşulu ile n X n büyüklüğündeki oyunlarda işe yarayacaktır.
Kaç tane olası tic-tac-toe oyunu var?
Aslında oyun sayısında bir üst sınır elde etmek kolaydır. İlk hamle için 9, ikinci için 8, üçüncü için 7 ve bu şekilde devam ederek 9! sonucuna ulaşılacaktır. Bu da 362.880 olası oyun anlamına gelecektir. Bu sayı küçük çocukları oyalamak için elimizde yeterince oyun olduğunu bizlere gösteriyor.
Ancak, bu iki nedenden dolayı doğru cevap değildir. Öncelikle, tahtayı döndürmek veya ters çevirmek sonucu hiçbir biçimde değiştirmeyecektir. Bu nedenle bazı oyunlar birden fazla kez sayılmış durumdadır. Yani aradığımız cevap 9!’den daha az olmalıdır. Aşağıda Şekil -1’de gösterdiğimiz oyunun döndürülmüş bir halini görüyorsunuz. Ancak sizin de fark etmiş olacağınız gibi aslında oyunlar aynıdır.
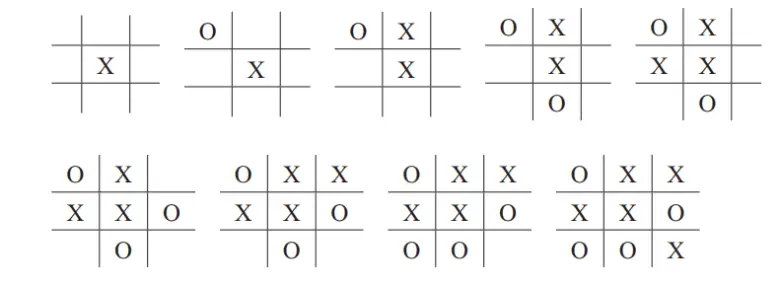
Peki o zaman şimdi kaç farklı oyun oynanabilir dersiniz? Cevap 3. 8!. Bu 3 sayısı ilk hamle için aslında 3 seçenek olmasından kaynaklanıyor. Sonuçta ilk işareti ya kenarlar üzerine, ya köşeler üzerine ya da ortaya koyabilirsiniz. Bu size 120960 sonucunu verecektir. Ancak elbette bu da oldukça büyük bir sayıdır.
Oyun teorisi açısından, tic-tac-toe, mükemmel bilgilerle oynanan, şans unsuru içermeyen ve sonlu bir oyundur. Bu, aşağı yukarı, her iki oyuncu tarafından da mükemmel bir mantıkla oynandığında bir tic-tac-toe oyununun her zaman bir beraberlik ile sonuçlanacağı anlamına gelir. Bu nedenle bu oyunu oynarken en büyük şansınız karşınızdaki rakibinizin oyunu iyi oynayamaması sonucunda olacaktır.

Bu arada son olarak hatırlatalım. Günümüzde bu oyunun çok çeşitli varyantları karşımıza çıkmaktadır. Bunlardan bir tanesi olan üç boyutlu üç taş oyununu yukarıda görebilirsiniz. Daha fazla varyant için bağlantıları inceleyebilirsiniz.
Kaynaklar ve ileri okumalar:
- Tic-tac-toe, the other way around!; yayınlanma tarihi: 2 Ekim 2014; Bağlantı: Tic-tac-toe, the other way around!
- How Old Is Tic-Tac-Toe?; Bağlantı: https://wonderopolis.org/wonder/how-old-is-tic-tac-toe
- Borovska, Plamenka & Lazarova, Milena. (2007). Efficiency of parallel minimax algorithm for game tree search. ACM International Conference Proceeding Series. 285. 14. 10.1145/1330598.1330615.
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel






