Öğrencilerin çoğunun baş belası olan kalkülüs aslında insanlık için bir nimettir. Kalkülüs denince de akla elbette matematiksel evrenin yapıtaşlarından olan türev ve integral gelecektir.
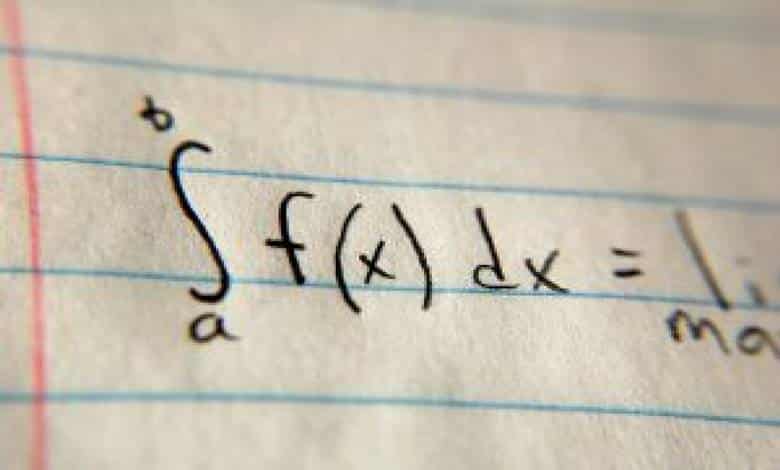
Kalkülüs özünde değişim ile alakalıdır. Örneğin, her gün ne kadar para aldığınızı ve harcadığınızı biliyorsanız, kalkülüs birkaç gün sonra ne kadar paranız olacağını anlamanıza yardımcı olur. Ya da birçok fizik probleminde olduğu gibi, hızını biliyorsanız bir arabanın durmasının ne kadar süreceğini hesaplayabilirsiniz.
Lüks kahve makineniz suyu tam olarak doğru sıcaklığa bu sayede getirir. Ne tür bir değişim olduğu önemli değildir. Çünkü hepsinin arka planında kullanılan matematik aynıdır. Türev, bir şeyin ne kadar hızlı değiştiğiyle, integral ise nicelikle, bir şeyin ne kadar değiştiğiyle ilgilidir. Bu iki kavram da yaşantımıza iki dev matematikçinin eş zamanlı çalışmaları sonucunda girmiştir.
İngiltere’de Newton ve Almanya’da Leibniz birbirlerinden bağımsız olarak bu kavramların temellerini attılar. Sonucunda ikisi de diğerinin tam olarak aynı fikre sahip olduğuna inanamadı. Şimdi tarih kitaplarına ilk kimin adı yazılmalıydı?
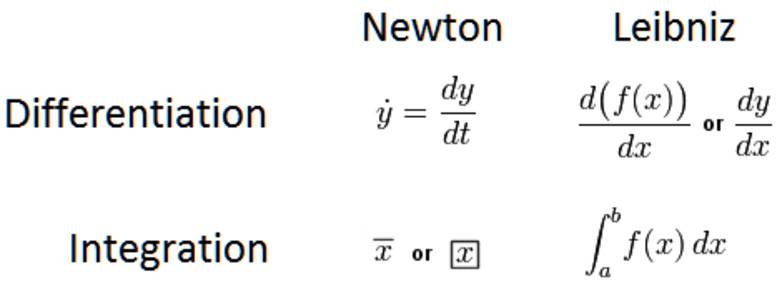
Bu konu ikilinin arasında uzun süre tartışılacaktı. Aslında ilk kimin keşfettiği bizim için pek de önemli değil. Aslında Newton ve Leibniz kalkülüsle uğraşan ilk kişiler değildi, ancak onu titiz bir sistem olarak geliştiren ilk kişilerdi. Kalkülüste birçok fikir Antik Yunan’da ve hatta ondan önce ortaya çıkmıştı. Ayrıca Hintli matematikçi Bhāskara, Leibniz’in fikirlerinin çoğunu 500 yıl önce zaten keşfetmişti.
Türev Nedir? İntegral Nedir? Birbiri İle Nasıl İlişkilidir?
Bir f(x) fonksiyonunun herhangi bir x0 noktasındaki türevi, fonksiyonun o noktadaki değişme hızını gösterir. Buna o noktadaki eğim de diyoruz. Ancak, türev aynı zamanda “türev alma” işlemini de ifade eder. Bu anlamda da bir eylem tanımlıyoruz.
İngilizce kullanımda, f ’(x) fonksiyonuna “derivative”, sürece de “differantiation” denir. Buradan hareketle de bizdeki kullanımda “türev” derivative, “türev alma” da differantiation anlamını taşımaktadır. Differantial kelimesi ise türevsel yani türevle ilgili olan demektir. Bu nedenle diferansiyel denklemler dediğimiz zaman içinde türev barındıran denklemler aklımıza gelmelidir.
Diferansiyel denklemler hesaplamak istediğimiz şeyi, küçük farklı parçalara (türevlere) ayırır ve bir andan diğerine nasıl değiştiğini incelerken, integral parçaları bir araya getirir (entegre eder) ve genel olarak ne kadar değiştiğini söyler. Aşağıda gördüğünüz Kalkülüsün temel teorisi de ikisini birbirine bağlar.
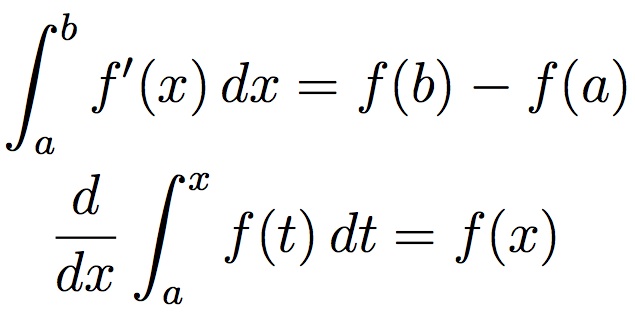
Kullandığınız toplam elektrik miktarı, beğendiğiniz adayın seçimde yeniden seçilme şansı, bir destek kirişinin ne kadar bükülebileceği. Fark etmez. Ne olursa olsun, bir şeyin ne kadar değiştiğini bilmek istediğimiz zaman integral kullanırız. Bir fonksiyonun integrali, o fonksiyona integral alma işlemi uygulandıktan sonra bulduğumuz fonksiyon ya da değer demektir.
Siz fark etseniz de etmeseniz de integral ve türev arabanızda, kahve makinenizde veya merkezi ısıtma sisteminizin termostatında, her an her yerdedir. Her yerde hesaplanması gereken değişimler vardır ve bunu bu ikili olmadan yapmak neredeyse imkansızdır.
Türev Ve İntegral Ne İşimize Yarar?
Bir araba fabrikasında matematikçi olarak çalıştığınızı düşünün. Göreviniz arabaları olabildiğince güvenli hale getirmek olsun. Bunu arabaları yakarak, ezerek, bir yerlere çarptırarak ölçebilirsiniz. Ama matematiği kullanarak işi çok daha ucuza da halledebilirsiniz.
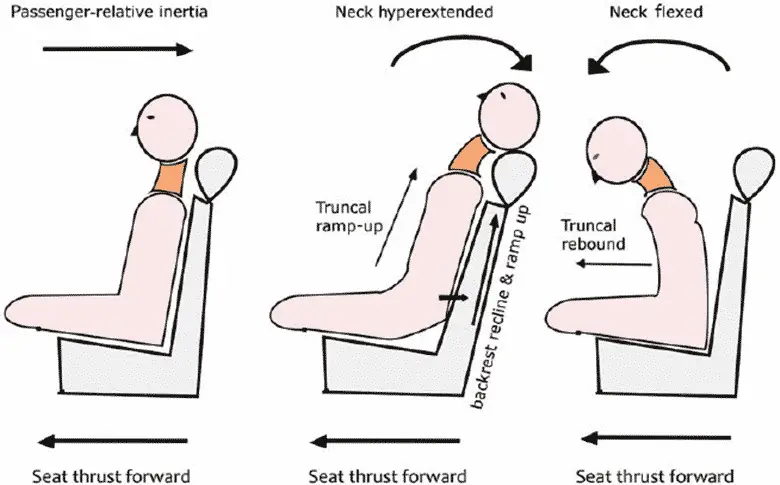
Bir araba kazasında, en büyük risk baş tarafımızdan yaralanmaktır. Çarpışma esnasında başın ileri ya da geri hareketi hayati olabilir. Aracın hızı bu hareketin şiddeti konusunda çok etkilidir. İşte bu hızı ölçmek için diferansiyel denklemler kullanabilirsiniz.
Diferansiyel denklem, bir ya da birden fazla fonksiyonu ve bunların türevlerini ilişkilendiren denklemdir. Bu denklemler yardımıyla çarpışmanın her anında, kafanın ne kadar hızlı hareket ettiğine bakabilirsiniz. Bu sayede de araca gerekli güvenlik donanımlarını önerebilirsiniz.
Bir matematikçi olarak, kafanın bir dizi anda ne kadar hızlı hareket ettiğini hesapladınız. Ama yine de kafanın hareket hızı ile çarpışmanın ne kadar tehlikeli olduğunu bilemezsiniz. İşte bu yüzden şimdi de integrale ihtiyacınız var. Tehlikeyi tanımlayabilmek için çarpışma sırasında toplamda kafanın ne kadar hareket ettiğini bulmanız lazım.
Diyelim ki bir saniyede öne arkaya iki kere hareket ettiğini buldunuz. Kaza toplam 4 saniye sürdü. 2 kere 4 toplam 8 hareket ediyor diyemezsiniz. Yapmamız gereken aslında basittir. Bir saniye bir kaza için büyük bir zaman dilimi. Oysa ki saniye yerine çok daha küçük zaman birimlerine bakıp, her zaman birimindeki hareketi belirleyip sonra da bunların toplamını alırsak çözümümüz gerçekçi olacaktır.
Bu arada bu verdiğimiz örnek bizim tarafımızdan uydurulmadı. Gerçekten de araba üreticileri, arabalarının güvenlik testlerinde bu hesaplamayı kullanıyorlar. Şimdi artık türev ve integral ne işe yararlar sorusu için kafanızda bir fikir oluşmuş olması lazım. Ama daha bitmedi. İntegralin geometri ile de ilişkili olduğunu hatırlarsınız.
Geometrik Anlamda Türev ve İntegral Nedir?
Aşağıdaki grafik herhangi bir şeyin zaman içindeki değişimini göstersin. Bu değişimi görebilmek için birbirine çok yakın iki noktayı incelememiz gerekir. Bu noktalar o kadar yakındır ki bir çizgi oluşturuyorlar gibi düşünebiliriz. Yani teğetin şekline bakarak karar verebiliriz. Teğet ne kadar “dik” ise, o kadar hızlı bir değişim var demektir, ne kadar yataysa, değişim o kadar azdır. Bu türevin geometrik anlamda karşılığıdır. Peki ya integral ne olacak?
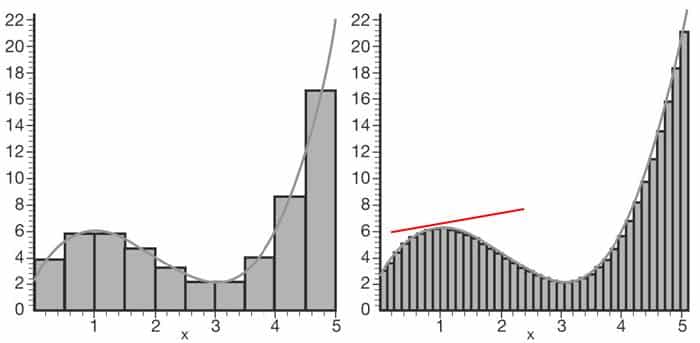
Aslında görsele dikkatli bakarsanız bir dizi adımla bir eğri altındaki alanın nasıl hesaplanacağını gösterir. Adımlar ne kadar küçükse, dalgalı şeklin altındaki bölgede o kadar az boşluk kalır. Kısacası çizginin altındaki alanı küçük dikdörtgenlere bölerseniz.
Her bir dikdörtgenin alanını hesaplar ve hepsini toplarsınız. Dikdörtgenler ne kadar küçükse, hesaplama o kadar doğru olur. Aynı şekilde hacmi de hesaplayabilirsiniz. Ancak bu biraz daha zor olacaktır. Prensip aynı olsa da hem dikey hem de yatay çalışmanız gerekir.
Türev ve İntegral Öğrenmesek Olmaz mı?
Peki türev ve integral öğrenmek zorunda mısınız? Aslında bu biraz da seçtiğiniz mesleğe göre değişir.
Günlük yaşamımızda bu ikilinin sağladığı avantajların tadını çıkartır ancak hesaplamaları biz yapmak zorunda kalmayız. Bu anlamda, matematiği kullanmanız gereken bir meslek seçmediğiniz sürece, integraller ve diferansiyeller hakkında detaylı bilgi sahibi olmanıza gerek yoktur.
Bilim, mühendislik, finans veya sosyoloji alanlarından herhangi birinde çalışıyorsanız, büyük olasılıkla bir noktada kalkülüsle karşılaşırsınız. Ancak ilgili bir meslek seçseniz bile hesaplamaları artık bilgisayarlar yapmaktadır.
Yine de bu durum size öğretilen şeylerden şikayet etmeniz anlamına gelmemelidir. Arka plandaki fikri başta anlamak zor gelebilir ama sembolik gösteriminin ürkütücü görüntüsünden uzaklaşır ve işin mantığını kavramaya çalışırsak anlamlandırmak çok daha kolaylaşır.
Doğal dünyada her şey sürekli değişir, bu yüzden onu incelemek için değişimi anlamanın bir yoluna ihtiyacınız vardır. Ve bunu kalkülüs başarmıştır. İntegral ve türev dünyayı değiştirdi. Bilgisayarları, akıllı telefonları, uçakları ve diğer birçok modern makineyi mümkün kıldılar. Onlar olmasaydı çok farklı bir dünyada yaşıyor olurduk.
Kaynaklar ve ileri okumalar :
- What is calculus and how to get the hang of it. Yayınlanma tarihi: 6 Mayıs 2023. Kaynak site ZME Science. Bağlantı: What is calculus and how to get the hang of it
- Maths in five minutes: Calculus. Yayınlanma tarihi: 22 Nisan 2022; Kaynak site: Plus Math. Bağlantı: Maths in five minutes: Calculus
Matematiksel