Bir dedektif olduğunuzu ve belli bir suçu çözmek için Sir Arthur Conan Doyle’un kurgusal karakteri Sherlock Holmes gibi tümdengelimli akıl yürütme becerinizi kullanmak zorunda kaldığınızı düşünün. Bir dakika. Yoksa onun kullandığı beceri tümevarımlı akıl yürütme miydi? Peki ama aralarındaki fark nedir?

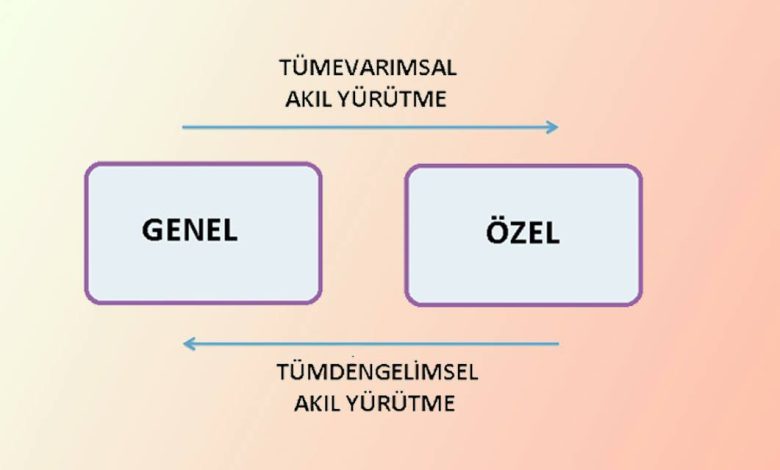
Tümdengelimli akıl yürütme ve tümevarımsal akıl yürütme, bilimsel araştırma yürütmeye yönelik iki farklı yaklaşımdır. Tümdengelimli akıl yürütmeyi kullanan bir araştırmacı, teorinin doğru olup olmadığını görmek için ampirik kanıtları toplayıp inceleyerek bir teoriyi test eder. Tümevarımsal akıl yürütmeyi kullanan bir araştırmacı, önce verileri toplar ve analiz eder, ardından bulgularını açıklamak için bir teori oluşturur.
Matematikte de gerçeklere deneyle, gözlemle değil, çoğu zaman akıl yürütmeyle ulaşılır. Bu nedenle akıl yürütmenin öğrenilmesi yalnız matematik eğitiminde değil, eğitimin her alanında vazgeçilemez bir gereksinimdir. Şimdi detaylar.
Tümdengelimli akıl yürütme nedir?
Tümdengelimsel olarak da bilinen tümdengelimli akıl yürütme, genellikle doğru olduğu varsayılan önermelere dayanarak bir sonuç çıkarmayı içerir. Eğer tüm öncüller doğruysa, o zaman sonucun da doğru olması gerektiği kabul eder. Matematiksel açıdan bunu şu şekilde düşünebilirsiniz: A=B, B=C, dolayısıyla A=C.
Birçok bilim insanı tümdengelimli akıl yürütmeyi bilimsel araştırma için altın standart olarak kabul eder. Bu yöntemi kullanarak, bir teori veya hipotez ile başlanır, ardından bu teori veya hipotezin belirli kanıtlarla desteklenip desteklenmediğini test etmek için araştırma yapılır. Ancak bu akıl yürütmeden günlük yaşamımızda sıklıkla faydalanılırız.
Tümdengelimli akıl yürütmede bir ilk öncül, ardından ikinci bir öncül ve son olarak bir çıkarım (akıl yürütme ve kanıta dayalı bir sonuç) vardır. Örnek olarak ” Çarpma işlemi toplama işleminden önce yapılmalıdır. Toplama işlemi çıkarmadan önce yapılmalıdır. Bu nedenle çarpma işlemi çıkarmadan önce yapılmalıdır. diyebiliriz. Benzer bir biçimde “Tüm örümceklerin sekiz bacağı vardır.” Tarantula bir örümcektir. Bu nedenle tarantulaların sekiz bacağı vardır.” da diyebiliriz.

Tümdengelimli akıl yürütmede sonucunda doğru çıkabilmesi için hipotezin sağlam olması gereklidir. Bu nedenle tümdengelim ile elde edilen sonuçlar öncüllerin doğru olması koşuluyla güvenilirdir.
Tümevarımsal akıl yürütme nedir?
Tümdengelimli akıl yürütme, gözlemlerle kanıtlanmış bir öncül ile başlarken, tümevarımsal akıl yürütme, belirli ve sınırlı gözlemlerden olası (ancak kesin olmayan) bir öncülü çıkarır. Tümdengelimli çıkarım genelden özele doğru giderken, tümevarımsal çıkarım özelden genele doğru gider. Tümevarımsal mantıkla yapılan bir sonucun güvenilirliği, gözlemlerin tamlığına bağlıdır.
Diyelim ki bir çanta dolusu bozuk paranız var; Torbadan üç madeni para çekiyorsunuz ve her bir madeni para bir lira geliyor. Tümevarımsal mantığı kullanarak, çantadaki tüm madeni paraların bir lira olduğunu öne sürerseniz hata yapabilirsiniz.
Doğru bir tümevarımsal akıl yürütme örneği şu biçimde olmalıdır. “Veriler: Çevremdeki insanlar hasta olduğunda ben de soğuk algınlığına yakalanma eğilimindeyim. Varsayım: Soğuk algınlığı bulaşıcı.” ya da ” Veriler: Karşılaştığım her köpek arkadaş canlısı. Varsayım: Çoğu köpek genellikle arkadaş canlısıdır.”

Bilimde ne tümdengelim ne de tümevarım mutlaka birbirine üstün değildir. Bunun yerine, gözlemlere mi yoksa teoriye mi dayalı tahminlerde bulunduğumuza bağlı olarak ikisi arasında sürekli bir etkileşim vardır.
Eğitimli Tahmin: Geriçıkarım Akıl Yürütme
Tümevarımsal ve tümdengelimli akıl yürütmeden ayrılan bir başka bilimsel akıl yürütme biçimi de dışaçekim olarak da adlandırılan geriçıkarım akılı yürütmedir.( İng: Abductive reasoning). Aslında günlük yaşamımızda en sık kullandığımız akıl yürütme biçimi de budur. Mevcut sınırlı bilgiden en olası sonucu belirlemek için tümdengelimli ve tümevarımsal akıl yürütmenin belirli yönlerini birleştirir.
Bu akıl yürütme biçimi de bir dizi gözlemle başlar ve veriler için mümkün olan en olası açıklamaya doğru ilerler. Genellikle net bir açıklaması olmayan bir olguyu gözlemledikten sonra bilinçli bir tahminde bulunmayı gerektirir. Örneğin bir mağazanın önünde tasmalı bir köpek görmek, sahibinin muhtemelen kısa bir süreliğine alışveriş yaptığını ve yakında geri döneceğini anlamamıza neden olur.
Bu akıl yürütme biçiminde ilk öncül kesindir. Ancak ikinci öncül net değildir. Dolayısıyla sonuç yalnızca olasıdır. Ancak yine de bu akıl yürütme biçimi test edilecek hipotezlerin oluşturulmasında faydalıdır. Aslına bakarsanız bu akıl yürütme bilimin temelini oluşturur. Sonucunda bilim insanları, ellerinde çoğu zaman yetersiz olan bilgiler üzerinden bir çıkarım yaparak ilerler. Çünkü ilerlemek için bazı şeyleri doğru kabul etmek gerekir. Bu yöntem kullanılarak da gelişmeler yaşanır.
Yazının devamında ayrıca göz atmak isterseniz: Teori = Kanıtlanmamış Fikir midir? Teori Kavramını Anlamak Neden Bu Kadar Zor?
Kaynaklar ve ileri okumalar
- Deductive reasoning vs. inductive reasoning. Yayınlanma tarihi: 30 Ocak 2023. Kaynak site: LiveScience. Bağlantı: Deductive reasoning vs. inductive reasoning
- Deductive versus inductive reasoning: what’s the difference. Yaınlanma tarihi: 30 Mayıs 2023. Kaynak site: ZME Science. Bağlantı: Deductive versus inductive reasoning: what’s the difference
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel