Tüm negatif ve pozitif tam sayıları toplarsak kaç eder? Diğer bir deyişle tüm tam sayıların toplamı kaçtır? Bu gibi sorular ilk bakışta çok basit görünür. Ancak ardındaki matematik oldukça şaşırtıcıdır.

Hepimiz sonsuz tane negatif ve sonsuz tane pozitif tam sayı olduğunu biliyoruz. Dolayısıyla tüm pozitif ve negatif tam sayıları topladığımızda 0 edeceğini düşünüyoruz. Çünkü pozitif ve negatif tam sayıların her ikisinden de sonsuz tane varsa, hepsi birbirini götürür ve 0 eder diye mantık yürütüyoruz.
Aslında bu şekilde düşünmemiz son derece doğaldır. Fakat işe matematiğin gözünden baktığımızda bu soruya çok net bir şekilde “0 eder” cevabını veremiyoruz. Bu durumun sebebini anlamak için birkaç matematiksel tanımla başlayalım.
Matematikte Dizi ve Seri Nedir?
Matematiksel kavramlar olarak ele aldığımızda dizi ve seri, çok önemli iki kavramdır. Dizi; sayıların belli bir sıra veya kurallar dizisi içinde grup veya ardışık olarak düzenlenmesidir. Seri ise, bir dizinin terimlerinin toplanmasıyla oluşturulur.
Diziler, sonlu ve sonsuz dizi olmak üzere iki gruba ayrılır. Seriler de dizinin sonlu veya sonsuz olmasına göre toplanarak bulunur. Örneğin 1, 3, 5, 7, 9, 11,… şeklinde 2 artarak devam eden örüntü, bir üst sınır verilmediği sürece sonsuza kadar devam eden bir dizidir. Bu tür dizilere aritmetik dizi deriz. 1 + 3 + 5 + 7 +… şeklinde yukarıdaki aritmetik diziyi toplarsak da bu dizinin bir serisini elde etmiş oluruz. Bu tür serilere de aritmetik seri deriz.
Bir başka örnek olaraksa i dizinin kaçıncı elemanı olduğunu göstermek üzere Pi = i2 kuralına uyan bir diziyi düşünebiliriz. Bu kurala uyan bir dizi P1 = 12 , P2 = 22 , P3 = 32,… şeklinde ilerleyen 1, 4, 9, 16, 25,… elemanlarından oluşan bir dizi olacaktır. Seri ise bu elemanların toplamı olacaktır ve ilk 5 elemanın toplamını genelde şu şekilde gösteririz:
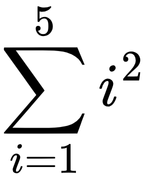
Fakat gördüğünüz gibi bu seri sonlu bir toplamdan oluşuyor. Peki ya sonsuz bir toplam söz konusu olsaydı? Bunun için incelememiz gereken iki matematiksel kavram daha var.
Bir Serinin Yakınsak veya Iraksak Olması Ne Anlama Gelir?
Serilerin belirli bir kuralı izleyen dizideki sayıların toplamı olduğunu öğrendik. Ancak daha önce de söylediğimiz gibi, söz konusu dizi her zaman sonlu olmayabilir. Yani sonsuz eleman içerebilir. Örneğin bir önceki bölümdeki Pi = i2 kuralına uyan diziyi sonsuza kadar devam ettirseydik, sonsuz serimizi şu şekilde ifade ederdik:
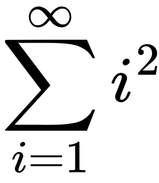
Sizce böyle bir serinin sonlu bir cevabı olabilir mi? Cevap hem evet hem hayır. Ve bu durumun başta sorduğumuz tüm negatif ve pozitif tam sayıları toplarsak kaç eder? sorusunun cevabıyla doğrudan bir ilişkisi vardır.
Sonsuz bir serinin yani sonsuz sayının toplamının sonucunu bulmak için önce sonlu bir toplam bulmamız gerekir. Ardından bu sonlu toplamın sonsuza giderkenki limitini alırız. Başka bir deyişle, toplamın tamamını n tane daha küçük toplamlara böleriz. Sonraysa bu kısmi toplamlara limit uygulayarak tüm serinin sonucunu elde ederiz.
Bunu yaptığımızda toplamı belirli bir sayıya çok yaklaşan bazı seriler vardır. Yani toplam devam ettikçe sonuç belirli bir sayıya yakınsamaya başlar. İşte böyle serilere yakınsak seriler deriz. Tam tersi şekilde toplamı hiçbir zaman belirli bir sayıya yakınsamayan seriler de vardır. Mesela bu serilerde toplam sonucu o kadar büyür ki, tüm sonsuz elemanların toplamı pozitif veya negatif sonsuza dönüşür. İşte bu serilere de ıraksak seriler deriz.
O Halde Tüm Negatif ve Pozitif Tam Sayıları Toplarsak Kaç Eder?
Yukarıda anlattıklarımızı göz önüne aldığımızda tam sayılar belirli bir kural izlediği için bir dizidir. Tüm negatif ve pozitif tam sayıların yani tüm tam sayıların toplamını bulmak istediğimiz için de elimizde bir seri var demektir.
İşte problemin zorlaştığı yer tam da burasıdır. Hatırlayın, az önce sonsuz bir serinin toplamını bulmak için kısmi toplamlardan yararlanabiliriz demiştik. Fakat bu kısmi toplamların sırası ve biçimi bazı durumlarda sonsuz bir serinin etkiler. Ve ne yazık ki, tüm negatif ve pozitif tam sayıları toplamak istediğimizde de olan budur.
Kısmi toplamlar yardımıyla pozitif ve negatif tam sayıları çok farklı şekilde gruplandırabiliriz. Ancak kolaylık olması açısından ilk akla gelen gruplama yöntemini ele alalım. Aşağıdaki toplamda birbirinin toplamaya göre tersi olan sayıları gruplandırarak limit aldık.
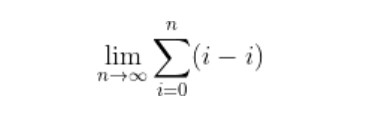
Toplamaya göre birbirinin tersi olan sayıları grupladığımızda sürekli 0 buluruz. Bu nedenle n sonsuza gittikçe limitimiz 0’a yakınsar. Dolayısıyla cevabımız 0’dır. Fakat bu sonsuz seriyi başka bir şekilde de gruplayabiliriz.
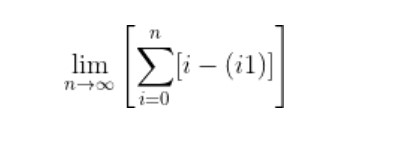
Sayıları birbirinin toplamaya göre tersi olacak şekilde değil de, mesela topladığımızda -2 edecek şekilde grupladığımızda sonsuz tane -2 elde ederiz. Ve n sonsuza giderken böyle bir limitin cevabı yoktur. Kısacası, tüm negatif ve pozitif tam sayıları toplarsak hem 0 eder hem de hiçbir şey etmez.
Kaynaklar ve İleri Okumalar
- If You Add All The Negative Integers With Positive Integers, Would You Get Zero? | ScienceABC ; Yayınlanma tarihi: 19 Ekim 2023
- Sequence and Series | CueMath
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel