Kilometrelerce devam eden, neredeyse tamamen durmuş bir trafikte sıkışıp kalmak, bir yaz tatiline başlamanın veya bitirmenin rahatlatıcı bir yolu değildir. Yol boyunca pineklerken çoğumuz trafik sıkışıklığının olmadığı bir geleceğin hayalini kuruyoruz.

Trafikte sıkışıp kaldığınız zamanlarda aklınıza gelen ilk şey matematik olmayabilir. Ancak trafik sıkışıklığının nasıl geliştiğini ve bunun nasıl önlenebileceğini anlamanın anahtarı aslında matematiktedir.
Trafik sıkışıklığı ile ilgili belki de en iyi bilinen (ve en şaşırtıcı) matematiksel sonuçlardan biri Braess paradoksudur. Bu paradoksa göre yeni yollar inşa etmek trafik sıkışıklığını artırır. Ayrıca mevcut yolların kapatılması ise trafik sıkışıklığını azaltır. Bunun nedeni, bir ağdaki arabaların dağılımının, genel olarak seyahat sürelerini azaltmak için bir grup olarak çalışmak yerine her birinin kendi kişisel seyahat sürelerini kısaltmaya yönelik hareket eden birçok sürücünün bireysel kararları tarafından belirlenmesidir.

Braess paradoksu bize, insanların modern bir şehirde verimli bir şekilde taşınmasında çok sayıda ilginç, matematiğin bulunduğunu hatırlatır. Örneğin, insanların seyahat sürelerini en aza indirmek için toplu taşıma nasıl planlanmalıdır? Sıkışıklığı azaltmak için trafik ışıkları nasıl çalıştırılmalıdır? Yeni yolları ne zaman ve nerede inşa etmeliyiz?
Trafik Sıkışıklığını Akışkanlar Mekaniği Yardımı İle İnceleriz
Tüm bu soruların cevaplarının arka planında matematik yer almaktadır. Çözüm için matematikçilerin ellerindeki en güçlü araç ise matematiksel modellerdir. Matematiksel analizde yoğun bir trafik bir akış olarak ele alınır ve sıvıların hareketini tanımlayan diferansiyel denklemler kullanılarak modellenir.
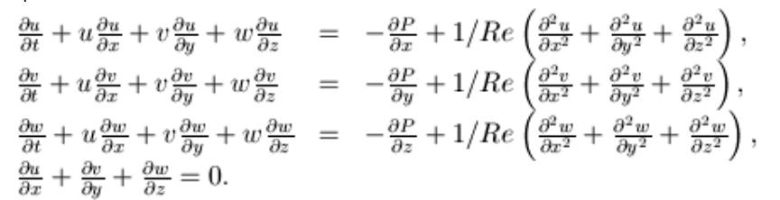
Akışkanlar mekaniği, akışkan olarak adlandırılan maddelerin (genel olarak sıvılar ve gazlar) fiziksel davranışlarını inceleyen bilim dalıdır. Çoğumuz “akışkan” kelimesini duyduğumuzda suyu düşünürüz. Ancak fizikçiler akışkanlıktan bahsettikleri zaman, kuş sürülerinden, bir kalabalıktaki yayaların hareketlerine kadar her şeyi bu kapsamda inceliyorlar. Trafik sıkıştığı zamanlarda da aynı bir sıvı gibi davrandığı için aynı kapsamda ele alınıyor.
Gözlemlere dayalı trafik akışının ilk basit tanımı 1933’te Amerikalı araştırmacı Bruce Greenshields tarafından yayınlandı. Bu, ilk Ford Model T’nin 1908’de üretilmesinden sadece 25 yıl sonraydı. Greenshields, trafiği ölçmek için sabit bir zaman aralığıyla ardışık resimler çekmişti. O zamandan beri, çok sayıda veri toplama ve modelleme tekniği geliştirildi.

Mevcut modellerin çoğu trafiği iyi tanımlasa da çok fazla hesaplama gücü gerektirir. Bu nedenle de gerçek zamanlı olarak trafik kontrolü için kullanmak zordur. Öte yandan bir başka sorun da bu modellerin insan psikolojisi faktörünün denklemlere dahil edilememesidir.
Denklemler, kuralların değişmediği iyi tanımlanmış problemleri modellemek için mükemmeldir ve bu nedenle bilimin omurgasını oluşturmuştur. Ancak günümüzün sürekli büyüyen, hızla değişen toplumunda birçok sorun tek bir denklemle modellenemeyecek kadar karmaşıktır. Trafik sıkışıklığı için polis kontrolü veya trafik kazası gibi ek faktörlere gerek olduğunu varsayabiliriz. Oysa ki trafik sıkışıklığı hiç yoktan kendi kendine de olacaktır.
Hayali Trafik Sıkışıklığı Neden Oluşuyor?

Özellikle büyük şehirlerde yaşayanların deneyimlediği garip bir durum daha vardır. Kalabalık bir yolda ilerlerken birden önünüzdeki trafik yavaşlar ve durmak zorunda kalırsınız. Bir süre bu biçimde adım adım ilerlersiniz ve sonra da mucizevi bir biçimde trafik açılıverir. Bu durum hayali bir trafik (phantom traffic jam) denilen bir fenomendir.
Bunun nasıl gerçekleştiğini anlamak için bir çalışma 2007 yılında yapıldı. Araştırmada yaklaşık 73 m çapında bir çemberin etrafında dolaşmak için 22 tane araba kullanıldı. Sürücülerden saatte 30 km’lik bir hızı korumaya çalışmaları ve arabalar arasında 10 metrelik bir boşluk bırakacak biçimde sürüş yapmaları istendi.

Deneyin başlangıcında arabalar kendilerine söylendiği gibi dönüşlerini gerçekleştirirken bir anda beklenmeyen bir durum gerçekleşti. Kameraların önüne denk gelen bölgede, yavaş yavaş arabalar kümelenmeye başladı. Tahmin ettiğiniz gibi sonrasında da trafik sıkışması oluştu. Daha sonra bu deneyin benzerleri yapıldığında sonuç yine aynıydı.
Düzgün bir trafik akışında, tüm araçlar otoyol boyunca eşit bir şekilde dağılmıştır. Sonucunda hepsi aynı hızda hareket eder. Bu koşullar altında, bu trafik akışı sonsuza kadar sürer.

Hayali bir trafik sıkışıklığı, rampalar, kavşaklar, şerit değiştirme vb gibi nedenler sonucunda yoğun trafikteki bir arabanın biraz yavaşladığı anda başlar. Bu yavaşlama aracın arkasındaki arabanın daha da yavaşlamasına neden olur. Sonuçta, yavaşlama eylemi bir dalga gibi geriye doğru yayılacaktır. Sonunda trafik ortada hiçbir sorun yokken durma noktasına gelir.
Sonuç Olarak
Bir dahaki sefere kendinizi tampon tampona trafikte bulduğunuzda kornaya basmak yerine biraz matematik düşünmeyi deneyin. Bu sadece akıl sağlığınızı korumakla kalmayacak, aynı zamanda zamandan da tasarruf etmenizi sağlayacaktır.
Kaynaklar ve İleri Okumalar:
- Saberi, M., Hamedmoghadam, H., Ashfaq, M. et al. A simple contagion process describes spreading of traffic jams in urban networks. Nat Commun 11, 1616 (2020). https://doi.org/10.1038/s41467-020-15353-2
- Traffic jams are contagious. Understanding how they spread can help make them less common. Yayınlanma tarihi: 7 Nisan 2020. Kaynak site: Conversation. Bağlantı: Traffic jams are contagious. Understanding how they spread can help make them less common
- Big Crowds Flow Like Water in Amazing (and Terrifying) Ways;. Yayınlanma tarihi: 4 Ocak 2019; Bağlantı: https://www.psychologytoday.com/
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel








