İçi boş bir küreyi herhangi bir yerini kesmeden ters yüz edebildiğinizi düşünün. Bu mümkün olmaz demeyin. Topoloji ile bu mümkündür. Peki ama adını son yıllarda oldukça sık duymaya başladığımız topoloji tam olarak nedir?

Bir şeyin top sayılması için mükemmel şekilde yuvarlak olması gerekmez. Futbol toplarında, golf toplarında ve tenis toplarında dikiş izleri ya da girintiler bulunur. Hatta Dünya bile mükemmel yuvarlak değildir. Çünkü üzerinde dağ sıraları vardır ve kutuplardan hafifçe basıktır. Yine de tüm bu nesneleri küresel olarak düşünürüz. Matematikte, bu tür şekil bozulmalarına gösterilen hoşgörü topoloji alanı tarafından ele alınır.
Topoloji Nedir?
Topoloji, iki nesneyi ancak biri diğerine yırtmadan ya da kesmeden dönüştürülebiliyorsa aynı kabul eder. Bu dönüşümde yalnızca bükme, germe ve sıkıştırma işlemlerine izin verilir. En bilinen örnek şudur: Topolojik açıdan bakıldığında, bir top bir kaseyle, bir simit de bir kahve fincanıyla aynıdır.

Eğer bir top ya da simit kilden yapılmış olsaydı, onları bükerek ve gererek sırasıyla bir kaseye ya da kahve fincanına dönüştürebilirdiniz. Ancak bir kaseyi, delik açmadan ya da yırtmadan kahve fincanına çeviremezsiniz. Bu durum, küre ya da simit gibi yüzeyler söz konusu olduğunda, iki nesneyi birbirinden ayıran şeyin delik sayısı olduğunu düşündürüyor. Ve bu gerçekten doğru.
Matematikçiler, akla gelen pek çok yüzeyin topolojik olarak ya bir küreye (sıfır delikli), ya bir simidin yüzeyine (teknik adıyla torus, bir deliklidir), ya da iki, üç ve daha fazla deliği olan toruslara denk olduğunu ispatladı.

“Akla gelen çoğu yüzey” ifadesiyle, kapalı ve yönlendirilebilir olan yüzeyler kastedilir. Kapalı olmak, yüzeyin bir kenarının bulunmaması demektir. Yani üzerinde yürürken dışarı düşebileceğiniz bir sınır yoktur. Yönlendirilebilir olmak ise, yüzeyin iki tarafının ayırt edilebilir olmasıdır. Başka bir deyişle, iç ve dış gibi birbirinden farklı iki yüzü vardır. Bu durum, yalnızca tek bir yüzeyi olan Möbius şeridinin tam tersidir. Matematikçilerin deliklerle neden ilgilendiğini anlamak için, topolojinin tarihine göz atmamız gerekir.
Şekilleri Topolojik Olarak Sıralamamızda Euler Karakteristiği Nedir?
1750 yılında Euler, tüm zamanların en güzel teoremlerinden birini ortaya koydu. Bir çokyüzlünün F yüzü, E kenarı ve V köşesi varsa, V – E + F = 2’dir.

Burada V köşe sayısı, F yüz sayısı ve E kenar sayısıdır. Örneğin, bir futbol topunda 20 beyaz altıgen ve 12 siyah beşgen parça vardır; toplamda 32 yüzey eder. Ayrıca 90 kenar ve 60 köşe bulunur. Gerçekten de 60 – 90 + 32 = 2 eder.
Bu basit gözlem, matematiğin birçok alanıyla derin bağlantılara sahiptir. Yine de bu sonuç, yüzyıllar boyunca Öklid, Arşimet ve Kepler gibi geometrilerin dikkatinden kaçtı. Çünkü bu sonuç geometrik değil, topolojiktir. Yalnızca şeklin yapısına bağlıdır.
Euler, çokyüzlüleri incelerken dolaylı olarak hepsinin dışbükey olduğunu varsaydı. Dışbükey demek, herhangi iki noktayı birleştiren doğru parçasının tamamen şeklin içinde kalmasıdır. Ancak kısa süre sonra araştırmacılar, Euler’in formülünün dışbükey olmayan bazı istisnalar için geçerli olmadığını fark etti.
Örneğin, 1813 yılında İsviçreli matematikçi Simon Lhuilier, bir çokyüzlüye delik açarak onu simit biçimine benzettiğimizde, yani topolojisini değiştirdiğimizde, formülün sonucunun V – E + F = 0 olduğunu gösterdi. İlginçtir ki, Euler ve Lhuilier çokyüzlüleri katı cisimler olarak hayal etse de, Euler’in formülü yalnızca sıfır boyutlu köşeler, bir boyutlu kenarlar ve iki boyutlu yüzeylerle hesaplanır.
Ayrıca, önemli olan sadece nesnenin topolojik yapısıdır. Bir çokyüzlüyü kilden yapıp kenarlarını kalemle işaretleyip sonra yuvarlayarak bir top şekline getirirsek, yüzeyler eğrilir ama sayıları değişmez. Bu nedenle, topolojik olarak bir küreye denk gelen her şeklin Euler sayısı 2’dir. Bir simit biçimindeki torus için bu değer 0’dır. Yassı bir disk için 1’dir. Her yüzeyin kendine özgü bir Euler sayısı vardır.
Euler’in formülünün bu topolojik yorumu ilk kez 1861 yılında Johann Listing tarafından yayımlanan bir makalede sunulmuştur. Bugün pek tanınmasa da Listing, “topoloji” terimini ilk kullanan kişidir.
Homoloji ve Betti Sayıları
Yaklaşık aynı dönemlerde Bernhard Riemann, karmaşık sayılarla ilgili çalışmaları sırasında ortaya çıkan yüzeyleri inceliyordu. Riemann, bir yüzeydeki deliklerin sayısını, yüzeyi iki parçaya ayırmadan kaç kere kesilebileceğini hesaplayarak belirleyebileceğimizi fark etti. Eğer yüzeyin sınırı varsa, örneğin iki uç kısmı açık olan bir pipet gibi, her kesik bir sınır noktasında başlayıp başka bir sınır noktasında bitmelidir. Bu bakımdan bir pipeti yalnızca bir kez, uçtan uca kesebiliriz; bu da pipetin tam olarak bir deliği olduğunu gösterir.
Eğer yüzeyin sınırı yoksa, örneğin bir simit gibi kapalı bir yüzeyse, ilk kesik aynı noktadan başlayıp aynı noktaya dönmelidir. Boş bir torusu iki kez kesmek mümkündür. Bu da torusun iki deliği olduğu anlamına gelir.

Henri Poincaré, topoloji çalışmalarını bir adım ileri taşıyan ve büyük ölçüde genişleten kişiydi. 1895 yılında yayımladığı çığır açıcı 123 sayfalık “Analysis Situs” adlı makalesiyle bu alanda derin izler bıraktı. Bu makalede ve onu takip eden beş devam yazısında, Poincaré, onlarca yıl boyunca gelişip meyve verecek çok sayıda topolojik fikri ortaya koydu.
Bunlar arasında en dikkat çekeni, homoloji kavramıdır. Homoloji sayesinde, pipet ya da klasör kâğıdındaki bir boyutlu halka benzeri deliklerden, İsviçre peynirinin içindeki iki boyutlu boşluklara ve daha yüksek boyutlara kadar farklı türdeki delikleri anlamayı hedefledi. Her bir boyuta karşılık gelen bu delik sayısını da, bir arkadaşı olan Enrico Betti’nin onuruna Betti sayıları olarak adlandırdı.
Topolojide Homoloji Nedir?
Homolojinin modern tanımı oldukça karmaşıktır. Ancak kabaca, her şekle belirli bir matematiksel yapı iliştirme yöntemidir. Bu yapıdan, Betti sayıları ya da Euler sayısı gibi daha basit bilgiler elde edebiliriz. Homoloji ve Betti sayılarını daha iyi anlamak için, birinci boyuta odaklanalım. Yani yüzey üzerindeki döngülere bakalım.
Döngüler yüzey üzerinde kayar, kendi üzerinden geçer, fakat yüzeyin dışına çıkamaz. Örneğin:
- Bir küre ya da düz disk gibi basit yüzeylerde, çizdiğin her döngüyü yavaşça büzerek bir noktaya indirebilirsin. Hiç kalıcı bir “delik” yoktur. Bu yüzden bu tür yüzeylerin homolojisi önemsizdir.
- Ama bir pipet gibi tüp şeklindeki bir cisimde, yüzeyde dolanan bir döngüyü bir noktaya büzemezsin. Döngü deliğin etrafında dolanır. Bu yüzden bu tür yüzeylerin homolojisi önemlidir.
Torusun üzerinde çok fazla döngü çizebilirsin. Döngüler yüzeyde dolanır, bükülür, karmaşık hale gelebilir.
Ama aslında her döngü, iki temel yol kullanılarak açıklanır. Birincisi, torusun ortasındaki delikten geçen bir döngü. Buna “a” diyelim. İkincisi, torusun tüpü boyunca dolanan döngü. Buna da “b” diyelim.
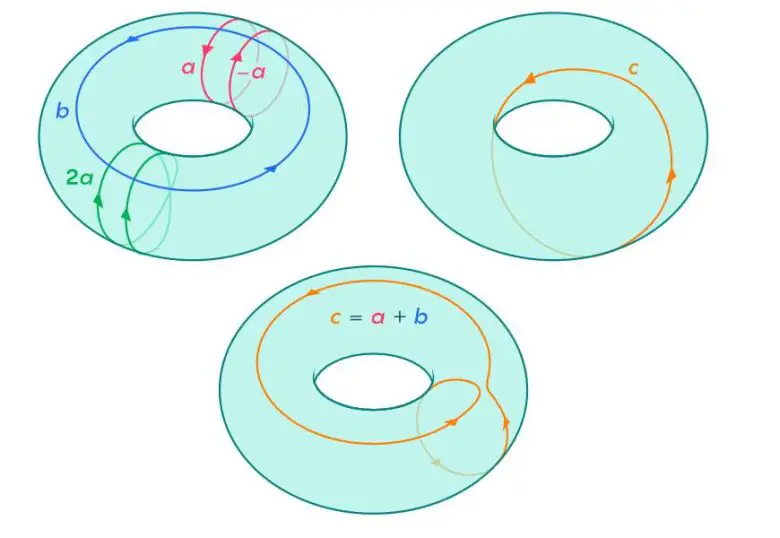
Bu iki temel döngü sayesinde torustaki tüm döngüler açıklanır.. Bir döngü “a” etrafında bir tur atıyorsa, bu a olur. İki kere a etrafında dönüyorsa, 2a olur. Bir tur “b” boyunca gidip sonra bir tur “a” boyunca gidiyorsa, a + b olur. Torusta iki bağımsız döngü vardır ve torusun birinci Betti sayısı (b₁) 2’dir.
Homolojinin grup yapısı, 1920’lerde Emmy Noether tarafından sistemli bir şekilde keşfedildi. Noether, grup ve diğer cebirsel yapıların öncüsüydü. Bu keşif sayesinde matematikçiler, topolojiyi anlamak için artık cebirin güçlü araçlarını kullanabiliyorlar.
Sonuç Olarak
Topologlar delikleri Betti sayıları ile sayar. Sıfırıncı Betti sayısı, nesnenin kaç parçadan oluştuğunu gösterir. Tek parça bir şekil için b0=1 olur. Birinci Betti sayısı, şeklin sahip olduğu dairesel deliklerin sayısını verir. Torusta iki yönlü dolanım vardır, o yüzden b₁ = 2.
İkinci Betti sayısı şeklin içinde kaç boşluk olduğunu söyler. Torusun bir iç boşluğu vardır, bu yüzden b₂ = 1 olur. Ve şaşırtıcı bir şekilde, bu sayılar Euler karakteristiğini de verir: Euler Sayısı=b0−b1+b2. Torus için hesap yaparsak: 1−2+1=0 olur. Bu sonuç Simon Lhuilier’in torus için bulduğu Euler sayısıyla tamamen uyumludur.
Matematikçiler yaklaşık bir yüzyıldır homolojiyi temel düzeyde anlıyorlar. Ancak cebirsel topoloji hâlâ aktif bir araştırma alanı olmayı sürdürüyor. Matematikçiler, şekillerin dijital temsillerinin homolojisini hesaplamak için teoriler ve algoritmalar geliştiriyor. Ayrıca, büyük veri kümelerinin — çoğu zaman yüksek boyutlu uzaylarda yer alan — altında yatan şekilleri belirlemek için yeni araçlar üretiyorlar.
Kaynaklar ve ileri okumalar için:
- Maths in a minute: Topology. Yayınlanma tarihi: 23 Mart 2022; Bağlantı: https://plus.maths.org/
- Penrose R. The topology of ridge systems. Ann Hum Genet. 1979 May;42(4):435-44. doi: 10.1111/j.1469-1809.1979.tb00677.x. PMID: 475332
- .Topology 101: The Hole Truth. Kaynak site: Quanta Magazine. Yayınlanma tarihi: 26 Ocak 2021. Bağlantı: Topology 101: The Hole Truth
Matematiksel





