
Gece gökyüzüne baktığımızda Evren karmaşık ve düzensiz gözükür. Ancak bu düzensizliğin içinde bile gözlerimiz bir düzen arar. İşte böyle bir düzenin varlığı bu yazıda sizlere aktaracağımız Titius-Bode Yasası tarafından ileri sürülür.
Günümüzde bu yasa bilim camiasında bir nevi numeroloji olarak kabul görse de gezegenler arasındaki yaklaşık mesafeyi pratik olarak hesaplamak ve matematiği hiç beklemediğimiz zamanlarda karşımıza çıktığına şahit olmamız açısından hala önemlidir.
Fikir 1772 yılında astronom Johann Daniel Titius tarafından ortaya atılacaktı. Kendisi, o dönem için bilinen gezegenlerin Güneş’ten ortalama uzaklıkları arasında bir ilişki keşfetmişti. Sonrasında 1778 yılında da Johann Elert Bode bu düzeni matematiksel bir dille ifade etti. Günümüzde bu ilişki artık ikisinin adıyla Titius-Bode Yasası olarak kabul ediliyor.
Titius-Bode Yasası her gezegenin Güneş’e olan uzaklığının kabaca kendinden öncekinin iki katı olması gerektiğini söylüyordu. Ancak hatırlatalım. O sırada ne Uranüs’ün ne de Neptün’ün varlığı bilinmiyordu. Uranüs 1781’e kadar ve Neptün 1846’ya kadar keşfedilmedi. Ayrıca bu yasa 2,8 AU mesafedeki bir gezegen için arama yapılması gerektiğini de savunuyordu.

Titius-Bode Yasası Nasıl Uygulanır?
İkilinin ortaya koyduğu modeli matematiksel olarak basit biçimde ifade etmeye çalışalım. İlk olarak işe sıfır ile başlayalım. Sonrasında bu sayıya bir ekleyelim ve her sayının iki katını alarak bir sayı dizisi oluşturalım. Bu durumda sayı dizimiz 0, 1, 2, 4, 8, 16, 32, 64, 128… biçiminde olacaktır.
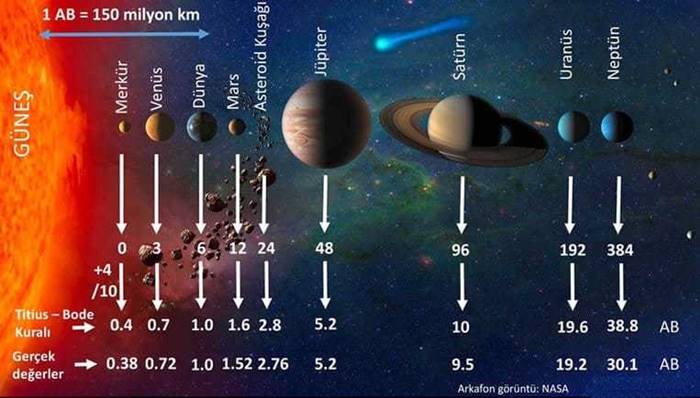
Şimdi bu dizideki her terimi önce 3 ile çarpın sonra da 4 ekleyin. Son durumdaki sayı diziniz ise 4, 7, 10, 16, 28, 52, 100, 196, 388, 772 biçiminde gözükmelidir. Şimdi de dizinin her elemanını 10’a bölün. Bu durumda aşağıdaki tablodaki değerleri elde etmiş olursunuz. Şu ana kadar yaptığınız şeyin size bir şey ifade etmemiş olması normaldir. İşin ilginç kısmı şimdi başlıyor zaten.
| 0,4 | 0,7 | 1,0 | 1,6 | 2,8 | 5,2 | 10,0 | 19,6 |
Gökbilimde uzaklıklar AB (astronomi birimi) cinsinden ifade edilmektedir. Güneş ve dünya arasındaki mesafe ise 1 AB olarak kabul edilmiştir. Buna dayanarak 1 AB = 149.600.00 km kadardır. Az evvel bahsettiğimiz ilginç durum yukarıdaki tabloda gördüğünüz sayıların AB ile olan bağlantısıdır. İlk gezegen olan Merkür’ün Güneş’e olan ortalama uzaklığı 0,387 AB’dir. Diğer gezegenler için de bu rakamların, gerçekten de gezegenlerin Güneş’e olan uzaklıkların yaklaşık değerleri olduğunu görebilirsiniz.
Titius-Bode Yasası Astronomlar Arasında Uzun Süre Revaçta Kaldı
13 Mart 1781’in gecesinde, astronom William Herschel, kendi yaptığı teleskopla, her zamanki gibi yıldızları araştırma girişimine başladı. Sonucunda Titius-Bode yasası 2,8 AB uzaklıktaki bir gezegenin daha var olması gerektiğini söylüyordu. Bahçesinde yalnız başına gözlem yaparken bir bir cismin yer değiştirdiğini ve diğer yıldızlardan daha önde gibi göründüğünü tespit etti.
Uranüs’ü gören herkes şimdiye kadar onu bir yıldız sanmıştı. Herschel ise ilk başta kuyruklu yıldız olduğunu düşündü. Bir süre gözlemledikten sonra da keşfettiği yıldızın Güneş’in etrafında döndüğünü fark etti. Herschel’in keşfettiği şey bir yıldız değil, antik çağlardan beri keşfedilen ilk gezegen olan Uranüs idi.

Titius-Bode Yasası 1781 yılında Uranüs’ün olması gereken uzaklıkta bulunmasıyla daha da değer kazandı. Uranüs gerçekten Satürn’e göre Güneş’ten yaklaşık iki kat daha uzaktaydı. Bunun üzerine astronomlar Mars ile Jüpiter arasında kuralın önerdiği gibi bir gezegenin varlığını araştırmaya başladılar.
Titius-Bode Yasasından cesaret alan gökbilimciler, Güneş’i Dünya’nın yörüngesinin yaklaşık 2,8 katı yarıçapında çevreleyen daha önce gözlemlenmemiş bir gezegen aramaya başladı. Sonunda 1801’de Giuseppe Piazzi bir tane buldu ve ona da Ceres adını verdi. Bu cüce gezegenin Güneş’e olan ortalama uzaklığı yaklaşık 2,77 AB idi. Devamında da aynı mesafelerde Pallas, Juno ve Vesta cüce gezegenleri keşfedildi.
Titius-Bode Yasası ufak sapmalar gösterse de evrenin belli bir düzene bağlı olarak oluştuğunu desteklediği için uzun yıllar bilim insanları tarafından kabul gördü. Ancak zaman geçtikçe bu yasanın güvenilirliği bozulacaktı. Bunun nedeni de 1846 yılında Neptün gezegeninin keşfiydi.
Yasa, gerçek mesafeye makul ölçüde yakın 38,8’lik bir mesafe öngörmüştü. Gerçek değer ise 30.1 kadardır. Uyum zayıf olsa da aslında yasa hala tam olarak bozulmamıştı. Bu arada hatırlatalım. Neptün teleskoplar yerine matematik yardımı ile keşfedilen ilk gezegendi.
Titius-Bode Yasası Plüton’un Keşfi İle Bozulacaktı
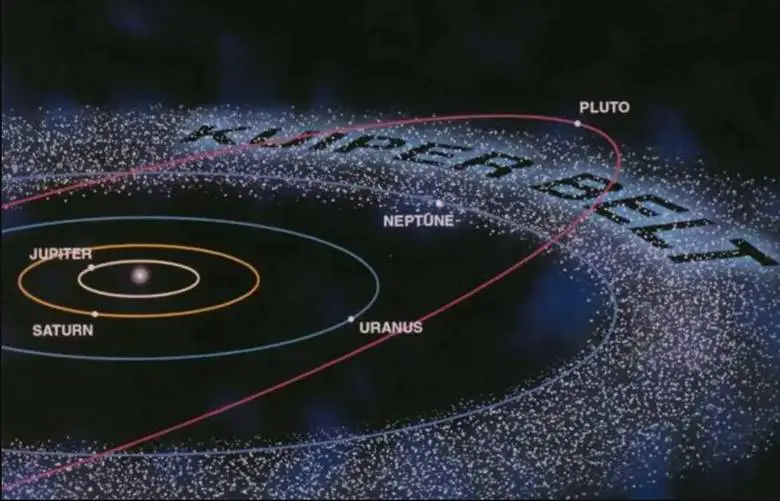
Sonucunda 1930 yılında da Plüton keşfedildi. Plüton’un Güneş’e olan uzaklığının Titius-Bode Yasası’na göre hesaplanan değeri (77,2 AB) gerçek değerinin (39,54 AB) neredeyse iki katı kadardı. Bu duruma göre Titius-Bode Yasası işe yaramamıştı. Gökbilimciler, Kuiper Kuşağı’nda zamanla Plüton boyutunda başka nesneler de bulmaya başladılar. Teknoloji gelişip daha işlevsel teleskoplar inşa edilince Güneş Sistemi’nin dış kısımlarındaki sönük gökcisimleri bir bir keşfedilmeye başlandı ve yasanın güvenilirliği ortadan kalktı.
Yıllar boyu, astronomide bu yasanın bir tesadüf olup olmadığı ya da Güneş Sistemi’ni yönlendiren önemli bir yasa olup olmadığı tartışıldı. Sonrasında da yasanın beynimizin kalıplar arama özelliğinin bir sonucu olduğuna karar verildi.
Görünüşe göre ilk bulguları sadece tesadüftü ve insanlar bariz bir modeli çok çabuk kavradılar. Bunun sonucunda günümüzde kimse Titius-Bode kuralını fazla ciddiye almıyor. Ancak bir süreliğine insanlığa kesinlikle yön gösterici olmuştu.
Kaynaklar ve ileri Okumalar:
- The Titius-Bode Formula; Bağlantı: https://www.spaceacademy.net.au/
- The expression that (nearly) explained the Universe; Yayınlanma tarihi: 1 Haziran 2009; Bağlantı: https://plus.maths.org
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel








