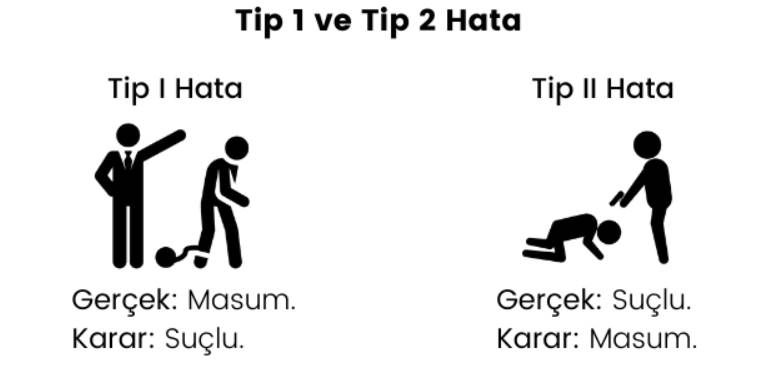
İstatistikte, hipotezleri test ederken olası iki tür istatistiksel sonuç hatası vardır. Bunlara Tip 1 ve Tip 2 hata denir.

İstatistik özellikle istatistik bilmeyenler için gerçekten kafa karıştırıcı bir branştır. Üstelik bir de sayılar ve semboller ile aranız iyi değilse bu daha da zorlayıcı bir durumdur. Oysa ki istatistik temelinde bir olasılık oyunudur. Ancak bu oyun dikkatli oynanmalıdır. Çünkü hesaplamalarda ne kadar küçük olursa olsun her zaman yanılıyor olma ihtimali vardır.
Bu bir çok farklı nedenlerden kaynaklanır. Kimi zaman neden sadece dikkatsizliktir. Ancak bazen de üzerinde çalışılan veriler hatalı olabilir. Bazen de hata bu verilerden yola çıkarak yapılan genellemelerdedir. Bu gibi hatalar nedeniyle istatistik ile uğraşırken çalışmaların istatistiksel olarak anlamlı olup olmadığını dikkate almak zorundayız. İstatistiksel anlamlılık, ölçülen değişkenler arasında bir ilişki olup olmadığını anlamamızı sağlar.
Bir veri setinin, rasgele olma olasılığının 1/20’den yani % 5 den az olması durumunda istatistiksel olarak anlamlı olduğu kabul edilmektedir. Ancak bu esnada da işin içine hata yapma ihtimali karışır. İstatistikte, hipotezleri test ederken olası iki tür istatistiksel sonuç hatası vardır. Bunlara Tip 1 ve Tip 2 hata denir.
Alternatif olarak, popülasyonda aslında yanlış olan bir sıfır hipotezi reddedilmezse, bir tip II hatası oluşur.
Bu tür bir hata, yanlış bir negatifin temsilcisidir.
Tip 1 Hata (Hatalı Pozitif) Nedir?
Boş hipotez diğer adıyla sıfır hipotezi gruplar ve değişkenler arasında hiçbir etkinin veya hiçbir ilişkinin olmadığı önermelerdir. Tip 1 hata, gerçek bir boş hipotezi yanlış bir şekilde reddettiğinizde oluşur. Bu hata tipine yanlış / hatalı pozitif de denir. Devam etmeden önce bir örnek verelim ve onun üzerinden ilerleyelim.
Bir araştırmacının, okul öncesi bir programa katılan ve katılmayan çocukların akademik başarılarında bir fark olup olmadığıyla ilgilendiğini düşünelim. Burada boş hipotez, iki grubun bazı başarı ölçütlerinde birbirine eşit olmasıdır.
Araştırdığımız şey ise, programa katılan çocukların ortalama puanının, programa katılmayan çocuklardan daha yüksek olmasıdır. İyi bir araştırmacı olarak göreviniz, iki grup arasında var olan herhangi bir farklılığın sadece okul öncesi deneyimden kaynaklandığını ve başka hiçbir faktörün bu işe karışmadığını göstermektir.
Şimdi, çeşitli tekniklerle, ebeveynlerin etkisi, ailedeki çocuk sayısı vb. gibi tüm olası farklılık kaynaklarını kontrol ettiğinizi ve ihtimalleri ortadan kaldırdığınızı düşünelim. Bu durumda, farklılıklar için olası tek açıklama okul öncesi deneyimin kendisi olacaktır. Ancak sonuçtan emin misiniz?
Ne yazık ki hayır! Birincisi, nüfus profilini her açıdan yansıtan bir örneği test ettiğinizden asla emin olamazsınız. Boş hipotezimiz iki grup arasında bir fark olmadığını söylüyordu. Ancak çalışmanızın sonucunda bir fark buldunuz. Ancak şu ana kadar sahip olduğunuz kanıtlara bakarak boş hipotezi reddederseniz, bir hata yaparsınız. Bu hataya Tip I hata denir. Tip-1 Hata; gerçekte bulgu iddiayı desteklemiyor olsa da, destekliyormuş gibi ileri sürme durumunda oluşur. Tip I hata başta belirttiğimiz anlamlılık seviyesi olarak da bilinmektedir.
Tip 2 Hata (Hatalı Negatif) Nedir?
Boş bir hipotez doğru veya yanlış olabilir. Ancak unutmayın, bunu asla bilemezsiniz çünkü boş değer doğrudan test edilemez. Ancak bir biçimde bu boş hipotezi reddetme ya da kabul etme durumunun seçmeniz gerekir. Bu durumda karşınıza 4 olası durum çıkar. Şimdi aşağıdaki tabloya bakalım.

Yapabileceğiniz başka bir tür hata daha vardır. Aslında tabloya baktığınız zaman bunu fark etmiş olmalısınız. Buna tip 2 hata denir. Bu durum bir araştırmacı, gerçekten yanlış olan bir boş hipotezi reddetmediğinde ortaya çıkar. Diğer bir deyişle, gerçekte bulgu iddiayı destekliyor olsa da, desteklemiyormuş gibi ileri sürme durumunda oluşur. Örneğin, örneklem grupları arasında gerçekten farklılıklar vardır. Ancak yanlışlıkla böyle olmadığı sonucuna varırsınız. Tip 1 ve tip 2 hata farkını anlamak için aşağıdaki örneğe de göz atabilirsiniz.

İdeal olarak, hem Tip 1 hem de Tip 2 hataları en aza indirmek istersiniz. Ancak bunu yapmak her zaman kolay veya kontrolünüz altında değildir. Aslında, Tip 1 hata seviyesi veya almak istediğiniz risk miktarı üzerinde tam kontrole sahip olursunuz. Ancak, Tip 2 hatalar doğrudan kontrol edilemez.
Bir testin istatistiksel gücü çok düşükse, genellikle II. tip bir hataya neden olur. İstatistiksel güç ne kadar yüksek olursa, bir hatadan kaçınma şansı o kadar artar. Genellikle, herhangi bir test yapılmadan önce istatistiksel gücün en az %80’e ayarlanması önerilir. Bu hatalar, bir örneklemdeki denek sayısına özellikle duyarlıdır; bu sayı arttıkça Tip 2 hata azalır. Yazının devamında göz atmanızı öneririz: Bilimsel Yöntem: Evrenin Sırlarını Çözmek İçin En Etkili Aracımız
Kaynaklar ve ileri okumalar:
- What are Type I and Type II Errors?; yayınlanma tarihi: 4 Temmuz 2019; Bağlantı: https://www.simplypsychology.org/
- To Err is Human: What are Type I and II Errors?; Bağlantı: https://www.statisticssolutions.com/
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel