Diyelim ki taşınma arifesindesiniz ve yoğun bir biçimde ev arama telaşındasınız. Tam istediğiniz evi bulduğunuzu düşündüğünüz sırada, aynı sokakta bir çok kiralık ev olduğunu fark eden bir arkadaşınız sizi uyarıyor. “Dikkat et, o caddede bir sıkıntı olabilir”. Muhtemelen arkadaşınız Teksaslı keskin nişancı yanılgısı adıyla bilinen bir hata yapıyor.
Abraham Lincoln ve John F. Kennedy, Amerika Birleşik Devletleri’nin yüz yıl arayla seçilen başkanlarıydı. Her ikisi de, John Wilkes Booth ve Lee Harvey Oswald adlı toplamda on beş harften oluşan üç isimle suikastçılar tarafından vurularak öldürüldüler. Katillerin ikisi de yargılanmadı. Her ikisi de Cuma günü eşlerinin yanında otururken öldürüldüler. Ayrıca Lincoln Ford Tiyatrosu’nda, Kennedy ise Ford tarafından yapılan bir Lincoln marka arabada öldürüldü.

Gerçekten benzerlikler ilgi çekici. Bu nasıl oluyor? Bir başka örnek verelim. 1898’de Morgan Robertson, Futility adlı bir roman yazdı. Titanik batmadan on dört yıl önce, hatta geminin inşasına başlanmadan on bir yıl önce yazıldığı düşünülürse, kitapla gerçek olay arasındaki benzerlikler ürkütücüydü.
Roman, herkesin batmaz olarak kabul ettiği Titan adlı dev bir gemiyi anlatıyordu. Aynı zaman da bu gemi, aynı Titanik gibi yüzen bir oteldi. Ancak olası bir felaket durumunda kullanılmak üzere, Titan’ın sadece yirmi cankurtaran sandalı vardı. Bu sayı ihtiyacın yarısı kadardı.

Ayrıca kitapta Titan, Nisan ayında Newfoundland’dan dört yüz mil uzakta bir buzdağına çarpıyordu. Titanik yıllar sonra aynı ayda aynı yerde aynı talihsiz kazayı yaşayacaktı. Sonucunda da Titan batacak ve Titanik’te olduğu gibi yolcuların yarısından fazlası ölecekti.
Kitapta ölenlerin sayısı ile gelecekteki kazada ölenlerin sayısı hemen hemen aynıdır. Benzerlikler burada bitmiyor. Kurgusal Titan ve gerçek Titanik’in her ikisinin de üç pervanesi ve iki direği vardı. Her ikisi de üç bin kişilik kapasiteye sahipti. Her ikisi de gece yarısına yakın buzdağına çarptı. Tüm bunlar şans mı yoksa öngörü mü?
Teksaslı Keskin Nişancı Yanılgısı Nedir?
Eğer tüm bunların tesadüf olmasının mümkün olmadığını düşünüyorsanız Texas sharp- shooter fallacy yani Teksaslı keskin nişancı safsatasını deneyimliyordunuz.

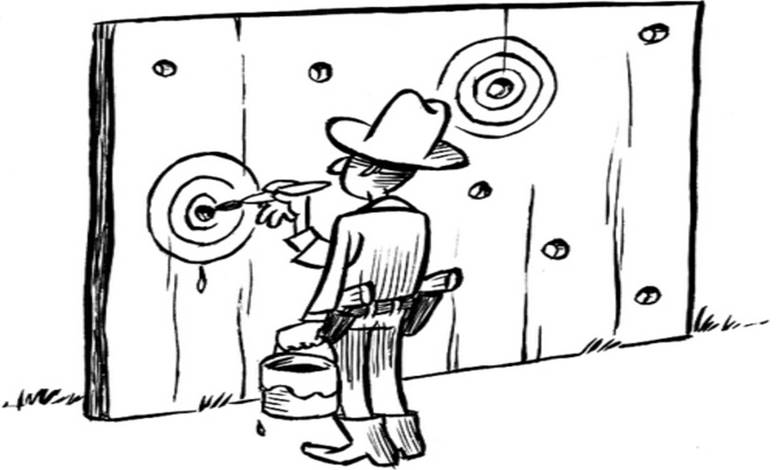
Öncelikle bu ilginç ismin nereden geldiğini kısaca aktaralım. Teksaslı bir kovboy, bir tepenin üzerinden, bir başka tepedeki ahıra doğru ateş etmektedir. Ahır o kadar uzaktadır ki, atışın yapıldığı tepeden açıkça görünen tek şey, orada bir ahırın olduğudur. Sonunda ahır kapısı deliklerle kaplanır ancak elbette bu delikler belirli bir nokta etrafında yoğunlaşmaz. Bunun üzerine kovboy, kurşun deliklerinin birbirine en yakın olduğu yeri merkezine alan bir hedef tahtası çizerek kendini keskin nişancı gibi gösterir.
Benzer bir biçimde, Titan ve Titanik arasındaki benzerliklere hayret ettiğinizde, romanda sadece on üç kişinin hayatta kaldığını ve geminin hemen battığını, Titan’ın birçok sefer yaptığını ve yelkenleri olduğu gerçeğini göz ardı ederseniz. Lincoln ve Kennedy bağlantıları sizi şaşırttığında, Kennedy’nin Katolik olduğunu ve Lincoln’ün Baptist olarak doğduğunu görmezden gelirsiniz. Ayrıca Kennedy tüfekle, Lincoln ise tabancayla öldürülmüştür. Kennedy Teksas’ta, Lincoln Washington’da vurulmuştu.
Teksaslı Keskin Nişancı Yanılgısı Neden Kaynaklanır?
Yukarıda verdiğimiz iki örnekte aslında bir çok farklılık vardı. Ancak biz sizin dikkatinizi benzerliklere çektik. Aslında bakarsanız bu yanılgı, insanların anlam aradığı her yerde karşınıza çıkacaktır. Teksaslı keskin nişancı yanılgısı aynı zamanda kümelenme yanılsaması olarak da bilinir ve ilk olarak epidemiyoloji -hastalıkların nüfus içinde dağılımı ve önlenmesi konusunu inceleyen bilim- alanında tanımlanmıştır. Sonrasında da psikologlar, bu türden hatalı düşünmenin başka alanlarda da ortaya çıktığını keşfetmiştir. Buna “küçük sayıların yasasına duyulan inanç” adını vermişlerdi.

Diyelim ki gazetede şu manşeti okuyorsunuz. “Yapılan son araştırmalar göre yeni kurulan işletmeler daha zeki elemanlar çalıştırıyor.” Bu haber size ne ifade eder? Umarız hiçbir şey ifade etmez, zira burada da yine küçük sayılar yasası yanılgısı söz konusudur. Sonucunda yeni kurulan işletmeler az sayıda eleman çalıştırma eğilimindedir. Dolayısıyla küçük işletmelerdeki ortalama zeka katsayısı büyük işletmelere oranla çok daha yüksek olacaktır.
Bu yanılgı bize, İnsanların benzerlikleri aradıklarını, farklılıkları görmezden geldiğini ve rastgeleliği hesaba katmadıklarını göstermektedir. Yedinci ayın yedinci gününde hayal ettiğiniz iş görüşmesi için Ankara’ya gittiğinizi düşünelim. Kaldığınız otelde oda numaranız da 362 olsun. Bu yanılgı sizin 3 + 6 – 2 = 7 işlemini yaparak, oda numaranızın uğurlu olduğunu düşünmenize neden olabilir.
Rastgele olaylarda örüntü görme eğilimi son derece insanidir ve evrimsel bir işlevi de bulunmaktadır. Hayatta kalmak için, atalarımızın her zaman tetikte olması gerekiyordu. Çevrelerinde gerçekleşen değişimlerin farkına varmak ve bunlara neyin neden olmuş olabileceğini düşünmek zorundaydılar. Bu sayede kendilerini neyin beklediğini öngörebileceklerdi.
Her şey aslında, insanların, küçük bir örneklemin anlamlı ve güvenilir bir sonuç üretebileceğini düşünme eğilimi ile ilgilidir. Oysa ki şans faktörünü elemek için daha büyük bir örnekleme ihtiyaç vardır (ahırın geri kalanını kaplayan diğer delikler gibi).
Sonuç Olarak
Bilim insanlarının bir hipotez oluşturup ardından yeni araştırmalarla çürütmeye çalışmasının nedenlerinden biri, Teksaslı keskin nişancı yanılgısından kaçınmaktır. Eğer bir bilgi, hipotezin kurulmasında kullanılıyorsa, ispatlanması için başka bilgilere dayandırılması gerekir. Bununla birlikte iddiaya kanıt gösterilen bilgilerin tarafsızca toplanması şarttır. İşine gelen bilgileri alıp, işine gelmeyenleri görmezden gelmek Teksaslı keskin nişancı yanılgısına düşmek demektir.
Kaynaklar ve ileri okumalar
- J.L.H. (Hans) Evers, The Texas sharpshooter fallacy, Human Reproduction. Volume 32, Issue 7, July 2017, Page 1363, https://doi.org/10.1093/humrep/dex103
- Texas Sharpshooter Fallacy. yayınlanma tarihi: 13 Temmuz 2020; Bağlantı: https://www.investopedia.com
- William C. Thompson, Painting the target around the matching profile: the. Texas sharpshooter fallacy in forensic DNA interpretation, Law, Probability and Risk, Volume 8, Issue 3, September 2009. Pages 257–276, https://doi.org/10.1093/lpr/mgp013
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel