Matematikçilerin hesaplamasına göre, Süper Lotoda bir ödülü garanti etmek için oynamanız gereken minimum kolon sayısı 27.

Manchester Üniversitesi’nden iki matematikçi, David Stewart ve David Cushing’in yaptığı çalışmaya göre, 27 kolon Süper Loto oynarsanız, en az 2 sayı oynadığınız kolonların birinde çekilişteki numaralar ile aynı olacak. Bu çalışma 27 kolon oynadığınız zaman büyük ikramiyeyi kazanacağınızı söylemiyor. Ancak 27 kolon ile herhangi bir ikramiye kazanacaksınız. Ancak aynı sonucu 26 kolon ile elde etmeniz mümkün değil.
Süper Loto Kazanma Olasılığı Nedir?

Milli Piyango tarafından düzenlenen Süper Loto, 1 ve 60 arasından 6 adet sayı seçmeye dayalı bir oyundur. Oyuncu bu 60 sayıdan 6’sını seçer. Seçtiğiniz her 6 sayı, bir kolon oluşturur. Sonra çekiliş gerçekleşir. 6 numaranın 6’sını da bilen büyük ikramiyeyi alır. 60 sayıdan 6 sayı seçildiği için C (60,6) tane seçenek var. Bu sayı 50 063 860’a eşittir, yani aşağı yukarı 50 milyon kadardır.
Dolayısıyla, lotoda bir kolon oynayarak 6 tutturma olasılığı 50 milyonda birdir. İki (değişik) kolon oynarsanız, 6 tutturma olasılığınızı 50 milyonda ikiye, yani 25 milyonda bire çıkarırsınız. On değişik kolon oynarsanız, 6 tutturma olasılığınız 5 milyonda bire yükselecektir.
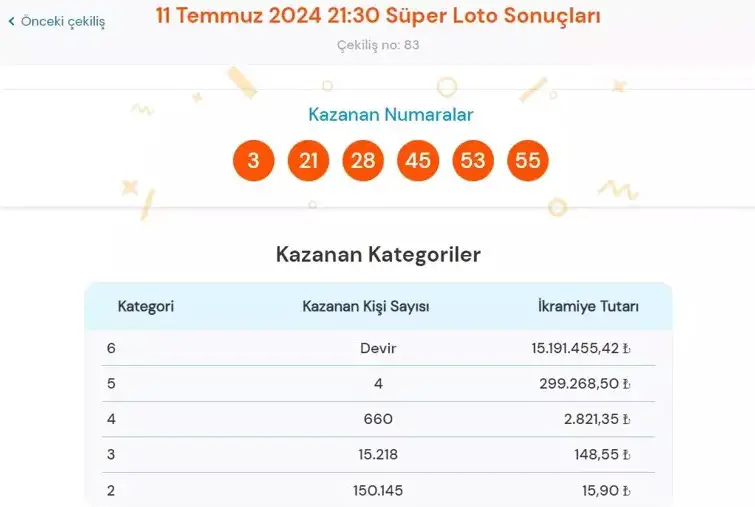
Süper Loto ile en az 2, en fazla 6 adet sayıyı doğru tahmin ederek farklı miktarlarda ikramiye kazanabilirsiniz. Eğer sadece 2 sayıyı tutturmayı hedefliyorsanız C (60,2)=1 770 olacaktır. ( Burada C kombinasyon hesabı anlamına gelir).
Şu an ki fiyatı ile hesaplarsak Süper Loto’nun kolon fiyatı 15 TL. En az iki sayıyı tutturmak için 27 kolon oynadığınızı düşünürsek ödemeniz gereken toplam para 405 lira. Görselde de en son çekilişte dağıtılan ikramiyeleri görüyorsunuz. Gördüğünüz gibi 2 ya da 3 sayı tutturarak zengin olmanız pek de olası değil.
Ancak yine de matematikçilerin bu sonuca ulaşmak için kullandıkları yöntem oldukça etkileyicidir. Ancak kendilerinin kullandıkları hesaplamalar son derece karmaşık olduğu için tüm detayları sizlere aktarmamız olası olmayacaktır. Matematikçiler bu sonuca ulaşmak için Fano düzleminden ve daha genel olarak projektif geometriden faydalandılar.
Hepimizin bildiği gibi paralel doğrular kesişmez ancak bazen kesişiyormuş gibi görünür. Bunun en basit örneği bir çift tren rayıdır. Eğer bu rayları takip ederseniz ufka doğru gittikçe iki rayın birbirine yaklaşıyor gibi göründüğünü fark edersiniz. Bu fikir doğrusal perspektifin temelidir ve matematikçilerin projektif geometri dedikleri şeyin kalbidir.
Fano Düzlemi Nedir?
Projektif geometri oluşturmada amaç, dış dünyanın gözümüze göründüğü gibi, perspektife uygun, paralel doğruların “sonsuzda” kesiştiği bir geometri oluşturmaktır. Bu da, Öklid düzlem geometrisine yeni noktalar (sonsuzdaki noktalar denir) ekleyip, doğru tanımında da bir değişiklik yaparak başarılabilir. Projektif düzlemin geometrisini tayin eden iki aksiyom vardır:
- Her bir nokta çifti, sadece tek bir ortak doğru içinde yer alır.
- Her bir doğru çifti, sadece tek bir ortak nokta içerir.
Bu aksiyomları sağlayan bir çok geometri vardır. Bunların en küçüğüne, mucidi Gino Fano’ya atfen Pano düzlemi denir. Bu, yedi çizgiyle üçerli olarak birleştirilmiş yedi noktadan oluşan bir sonlu geometridir ve aşağıdaki gibi gözükür. Fano düzleminde her doğru üzerinde 3 nokta vardır. Her noktadan 3 doğru geçer. ( Ortadaki çemberi de bir doğru olarak kabul ederiz.)
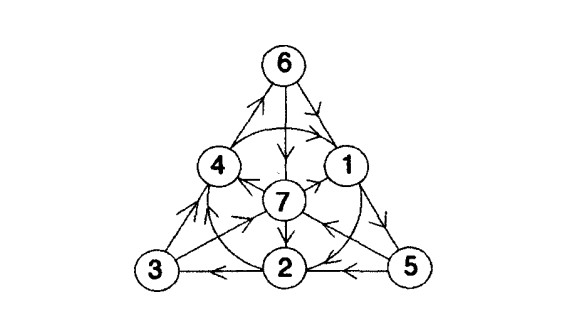
Yedi topla düzenlenen bir loto çekilişi olduğunu varsayalım. Ayrıca büyük ikramiye için üç numara gerekiyor olsun. Fakat bu lotoda üç sayıdan ikisini tutturduğunuzda da bir ödül kazanıyorsunuz. Yukarıdaki örnekteki sayıları listelersek 346, 615, 523, 574, 371, 672 ve 412 biçiminde 7 tane sayı elde edebiliriz.
Bu sayılar ile bir kupan oynarsanız en az iki sayı tutturma olasılığınız kesin olacaktır. Çünkü her bir sayı çifti tek bir doğruda yer almaktadır. Loto çekilişinde 3, 5 ve 6 çıktığını düşünelim. İçinde 3 ve 5; 5 ve 6 ve de 3 ve 6 olan iki sayı Fano düzleminde aynı doğru üstünde yer alacaktır. Yani bu düzlem yardımı ile oluşturduğumuz loto kuponları en az iki sayıyı garanti edecektir.

Fano düzlemi loto tahmininde kullanılsa da temelde oktonyonların çarpma kurallarını özetlemeye yarar. Gerçel sayılar bir boyutlu, karmaşık sayılar iki boyutlu, kuaterniyonlar dört boyutlu, oktonyonlar sekiz boyutlu hiperkompleks sayılar olarak kabul edilmektedir.
Süper Lotoda Kazanmak İçin Gereken Kolon Sayısı Nasıl Hesaplandı?
Sezgilerimize oldukça aykırı olan bu geometri günümüzde matematikçiler tarafından pek çok farklı hesaplamada kullanılmaktadır. En ilgi çekici kullanılma yerlerinin arasında da şans oyunları ile ilgili hesaplamalar gelir. Bu kısa ön bilgiden sonra şimdi süper loto için yapılan hesaplamalara geri dönebiliriz.
Matematikçiler çözüm için Fano düzleminin her bir noktasına bir sayı çifti atadı. Böylece bir doğru üzerinde 3 sayı çifti yani altı sayı oldu. Bu altı sayı ise bir kolon anlamına geliyor. 1 den 60’a kadar bu biçimde bir eşleşme yaptıktan sonra aşağıdaki görselde gördüğünüz sonuca ulaştılar. Bu durumda 3 Fano düzlemi ve 2 üçgen gerekti. Bu da toplamda 7×3 +3×2= 27 kolon oynamanız anlamına geliyordu.

Sonuç Olarak;
Loto oynayan çoğu insan, büyük ikramiyeyi kazanamayacaklarına dair en azından sezgisel bir anlayışa sahiptir. Ancak yine de “neredeyse kazanma”nın garip bir cazibesi vardır. Çünkü her ne kadar olasılıklar çok büyük sayılardan oluşsa da yine de kazanan birilerinin olduğunu düşünmek arka plandaki itici gücü oluşturur.

Sonucunda her zaman piyango kazananlar hakkında hikayeler duyar ve okursunuz. Büyük ikramiye kazananlar haberlere konu olur, ancak yıllar boyunca oynayıp da kazanamayan savaşçıları kimse hatırlamaz.
Kaynaklar ve ileri okumalar
- Mathematicians find 27 tickets that guarantee UK National Lottery win. Yayınlanma tarihi: 29 Eylül 2023. Kaynak site: New Scientist. Bağlantı: Mathematicians find 27 tickets that guarantee UK National Lottery win
- Cushing, David & Stewart, David. (2024). Applying constraint programming to minimal lottery designs. Constraints. 1-21. 10.1007/s10601-024-09368-5.
- How many lottery tickets do you need to buy to guarantee a win? Mathematicians find the answer. Yayınlanma tarihi: 3 Ağustos 2023. Bağlantı: How many lottery tickets do you need to buy to guarantee a win? Mathematicians find the answer
- A Few of My Favorite Spaces: The Fano Plane. Yayınlanma tarihi: 24 Ekim 2015. Kaynak site: Scientific American. Bağlantı: A Few of My Favorite Spaces: The Fano Plane
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel