“Güven, ama doğrula.” Bu ifade, başkalarına güvenme gereği ile kontrolü tamamen elden bırakmama isteği arasındaki hassas dengeyi anlatır. Matematikçi Adi Shamir, kendi adıyla bilinen “Shamir’in sır paylaşımı” algoritmasını geliştirirken, büyük olasılıkla tam da bu gerilimi hedef alıyordu.

Bu algoritmayı kavramak için önce bir bulmaca düşünelim: Yaşlı bir kadın, şifreli bir kilitle korunan kasasında değerli eşyalarını saklıyor ve bunları beş oğluna miras bırakmak istiyor. Ancak her birinden şüphelendiği için, şifreyi yalnızca birine vermeye cesaret edemiyor. Oğullarından biri şifreye tek başına ulaşırsa, tüm eşyaları alıp kaçabileceğinden endişe ediyor.
Bu riski azaltmak için, her oğluna yalnızca bir parça bilgi vermeyi planlıyor. Fakat bu ipuçları öyle düzenlenmeli ki, ancak beş kardeş bir araya gelirse kasayı açabilsinler. Peki, böyle bir durumda kadın ne yapmalı?
İlk bakışta görev basit görünür. Kadın, şifrenin beş basamaklı olduğunu varsayarak her oğluna birer rakam verir ve böylece beş kardeş birlikte şifreyi oluşturur.
Ancak bu plan ciddi bir zafiyet içerir. Eğer üç oğul güç birliği yaparsa, geriye sadece iki eksik rakam kalır. Bu iki bilinmeyeni deneme-yanılma yöntemiyle kolayca bulabilir ve diğer iki kardeşi tamamen devre dışı bırakabilirler.
Kadın bilgiyi öyle bir biçimde dağıtmalı ki, yalnızca beş kardeş birlikte hareket ettiğinde şifre ortaya çıksın. Eğer içlerinden sadece ikisi, üçü ya da dördü bir araya gelirse, ellerindeki bilgiler hiçbir işe yaramasın. İşte bu gereklilik, basit görünen bu görevi karmaşık ve yaratıcı bir çözüme ihtiyaç duyan bir probleme dönüştürüyor.
Shamir’in Sır Paylaşımı Algoritması Nedir?

1979 yılında Adi Shamir, karşılaştığı zorluğa rağmen geri adım atmadı. Geliştirdiği yöntem gerçekten sıra dışıydı. Shamir’in Sır Paylaşımı Algoritması, modern kriptografi ve veri güvenliği alanlarında devrim niteliğinde bir çözüm sunar.
Kritik bilgilerin güvenli biçimde saklanmasını ve paylaşılmasını sağlayan bu algoritma, hem matematiksel kesinliği hem de sağladığı esneklikle öne çıkar. Shamir’in yöntemini daha iyi anlamak için somut bir sayısal örnek üzerinden ilerleyelim:
Kadının kasasının şifresi 43953 ve sadece iki oğlu var. Kadın bir oğluna “439”, diğerine ise “953” verirse, her biri şifrenin yalnızca bir kısmını öğrenmiş olur. Ancak bu durumda, iki kardeşin iş birliği yapmasına gerek kalmaz. Onları birlikte çalışmaya zorlamak için daha farklı bir yaklaşıma ihtiyaç vardır.
Hepimizin bildiği gibi, iki noktadan yalnızca bir doğru geçer, ancak tek bir noktadan sonsuz sayıda doğru geçebilir. Bu temel ilke, Shamir’in matematiksel çözümünün temelini oluşturur.
Diyelim ki kadın kafasında şu doğrusal denklemi belirledi: y = 5x + 43953. Büyük oğluna, bu doğru üzerindeki P₁ = (33503, 211468) noktasını; diğer oğluna ise P₂ = (85395, 470928) noktasını verdi.
Çocuklar matematikte çok iyi olmasalar bile, bu iki noktayı koordinat düzlemine yerleştirip aralarına cetvelle bir doğru çizerek, doğrunun y ekseniyle kesiştiği noktayı kolayca bulabilirler. Bu kesişim noktası, yani doğrunun y-eksenini kestiği noktanın y-değeri, kasanın şifresidir: 43953.
Ya Kadının Daha Fazla Çocuğu Varsa?
Kadının iki değil üç çocuğu varsa da aynı yöntem çalışır. Ancak bu durumda kadının şifreyi gizlemek için düz bir çizgiyi değil, bir parabolü seçmesi gerekecektir. Diyelim ki kadın y = 5x2 + 10x + 43953 fonksiyonunu seçip oğullarının her birine parabol üzerinde bir nokta vermiş olsun. Bu denklemin de y ekseniyle kesişme noktası istenen çözüme yani 43953 sayısına karşılık gelecektir.

Ancak bu durumda da çocuklardan ikisi birleşip üçüncüye karşı komplo kuramaz. Çünkü iki noktadan da sonsuz sayıda parabol geçer. Bu durumda y ekseni ile kesişme noktasını ve dolayısıyla kasanın şifresini bulmak için üçüncü kardeşin yardımı her türlü gereklidir.
Aynı mantıkla devam edersek, dört oğlu olan bir kadın, y = ax3 + bx2 + cx + 43953 türünde bir denklem ile şifreyi saklayacaktır. Beş oğlu olan bir kadın da dördüncü dereceden bir polinom denklemi kullanır (örneğin, y = ax4 + bx3 + cx2 + dx + 43953) vb.

Ama bir sorun var. Beş çocukla ilgili senaryoya geri dönelim. Eğer dördü bir araya gelip, diğer kardeşe komplo kurarsa, dört noktayı kullanarak dördüncü derece denklemi basitleştirebilirler. Şifreyi tam olarak bulamasalar da sonunda iki bilinmeyenli bir denklemle karşı karşıya kalırlar.
Bu denklemde bilinmeyen olarak a parametresi ve c yani aradığımız şifre vardır. Ayrıca bu çocuklar c’nin yani şifrenin pozitif bir tamsayı olduğunu biliyorlar. Ayrıca kadının yaşı vb gibi unsurları dikkate alarak a parametresinin de pozitif tamsayı olması gerektiğini varsayabilirler.
Bu da olasılık aralığını önemli ölçüde kısıtlamaktadır. Kardeşler farklı çözümleri denemek için bir bilgisayar programı kullanırsa kısa sürede şifreyi bulacaklardır.
Shamir’in Sır Paylaşımı Güvenliği Nasıl Sağlar?
Böyle bir sorunu aşmak için Shamir’in elinde başka bir numara daha vardı. Hesaplamaları alışık olduğumuz gerçek sayılarla yapmak yerine, daha sınırlı bir sayı evrenine geçti: sonlu cisimlere. Bu sayı sisteminde toplama, çıkarma, çarpma ve bölme işlemleri aynen bildiğimiz gibi çalışır.
Ancak kritik fark şudur. Sayılar sonsuza kadar uzanmaz. Bu evrende sınırlı sayıda eleman vardır. Bu kısıtlama, hem matematiksel belirsizlikleri ortadan kaldırır hem de işlemleri denetim altında tutar.
Bu yaklaşım ilk bakışta yabancı gelecektir. Oysa sonlu sayı sistemlerini günlük hayatta zaten kullanırız. Saat bunun en tanıdık örneğidir. Saatleri yalnızca 12 ya da 24 değerle sınırlı bir aralıkta düşünürüz. Buna rağmen bu sistem içinde sorunsuzca hesap yaparız.

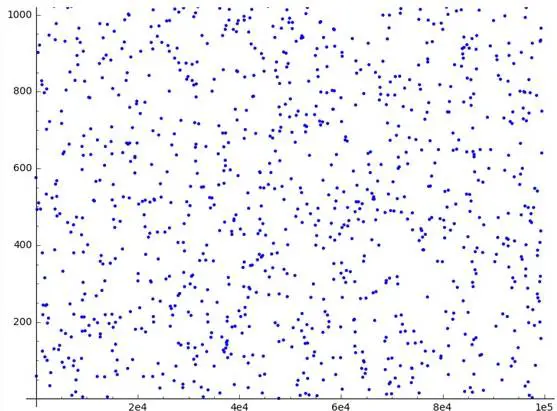
Shamir’in sır paylaşımı da aynı mantıkla çalışır. Hesaplar, sınırları önceden belirlenmiş bir sayı aralığında yapılır; bu sınır genellikle büyük bir asal sayıdır. Böyle bir uzayda polinomlar artık düzgün, kesintisiz eğriler çizmez; düzlemde dağınık görünen noktalar üretir. Bu da hem yapıyı dışarıdan okunamaz hâle getirir hem de sırrın ancak yeterli sayıda parça bir araya geldiğinde ortaya çıkmasını garanti eder.
Sonuç olarak
Kadın hesaplarını böyle sınırlı bir sayı aralığında yaptığında, kardeşlerin birbirlerine karşı komplo kurması imkânsız hâle gelir. Doğru sayısal kodu elde edebilmek için tek seçenekleri birlikte hareket etmektir.
Günümüzde Shamir’in Sır Paylaşımı algoritması, gizli bilgilerin güvenilmeyen ağlar üzerinde güvenli biçimde dağıtılmasını sağlayan temel kriptografik yöntemlerden biri olarak kullanılmaktadır.
Kaynaklar ve ileri okumalar
- Shamir, A. (1979) How to Share a Secret. Communications of the ACM, 22, 612-613.
http://dx.doi.org/10.1145/359168.359176 - How Cryptographic ‘Secret Sharing’ Can Keep Information Safe. Yayınlanma tarihi: 7 Aralık 2023. Kaynak site: Scientific american.Bağlantı: How Cryptographic ‘Secret Sharing’ Can Keep Information Safe
Matematiksel





