Bir sayının ( 0 hariç) sıfırıncı kuvvetinin bir çıktığını hepimiz biliyoruz. Üslü sayıları ilk öğrendiğimiz zamanlarda verilen bir kuraldır bu. Ancak bunun nedeni hakkında bir çoğumuzun bilgisi yeterince yoktur. Genellikle birileri öyle kabul etmiş der, sonrasında ezberler ve geçeriz.
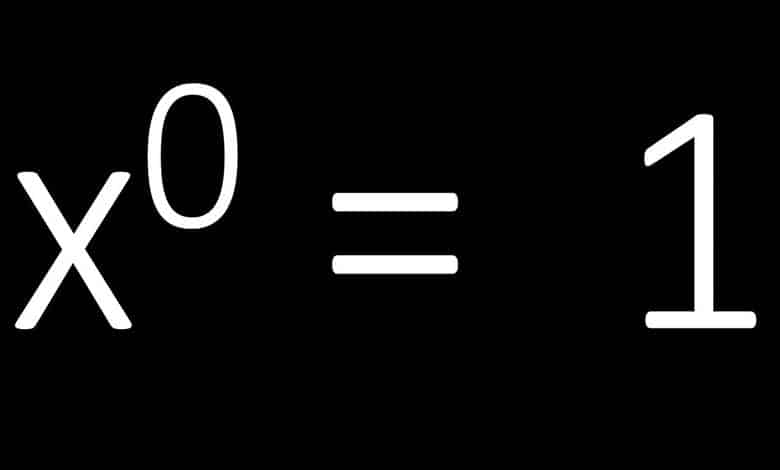
Matematikçiler belli tanımlar yaparken, yapılan o tanımın içinde bulunduğu sisteme uygun ve tutarlı olmasına, sorun yaratmamasına dikkat ederler. Temel olarak sayının sıfırıncı kuvvetinin bir olmasının nedeni de budur. Diğer bir deyiş ile bu bir kabuldür. Ancak bunun nedenini tam olarak anlamak için çoğu zaman pek kullanmak zorunda kalmadığımız kavramsal bilgiye ihtiyaç vardır.
Hemen herkesin bildiği gibi üslü sayılar çarpma işleminin kısaltılmış gösterimidir. Modern üstel gösterim 16. yüzyılda kabul görmeye başlasa da üslü sayıların kuralları esasen çok daha öncesinde, Arşimet tarafından tanımlanmıştır.
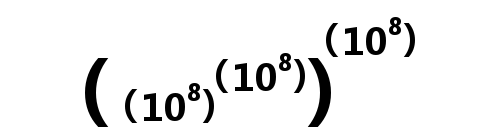
Modern sayı sistemimizde büyük sayıları kullanmak ve yazmak kolaydır. Ancak harflerin sayılara dönüştüğü ilkel bir sistem olan Yunan sayı sistemi ile bunu yapmak imkansızdı. Bu durumdan yılmayan Arşimet, kendi sayı sistemini geliştirmişti. The Sand Reckoner [Kum Hesaplayıcısı] adlı incelemesinde Arşimet, bütün evreni doldurmak için gereken kum tanesi sayısını bu sayede hesaplamayı başarmıştı.
Bir şeyin yokluğunu temsil eden bir sayıyı kavramak zor bir kavramdır. Bu nedenle sıfır sayısı hayatımıza en son giren tamsayıdır. Bir hiçlik olarak kabul gören sıfırın sayı olarak kullanımına MS 7. yüzyılda Hintli bir matematikçi olan Brahmagupta (598–668) öncülük etmiştir.

Ancak genel kabulü de kolay olmamıştır. Aslında sıfır sayısı sayı doğrumuza ancak 1600’lerde İngiliz matematikçi John Wallis’in önerisi ile dahil edilmiştir. Bu nedenle matematiğin bir çok kuralı da sıfır sayısının yokluğunda gelişmiştir. Şimdi asıl konumuza geçebiliriz.
Bir Sayının Sıfırıncı Kuvvetinin Bir Olmasının Nedenleri
Öncelikle ilk olarak konuya üslü sayıların kuralları çerçevesinden bakalım. Bildiğiniz gibi üslü sayıların çarpımı esnasında tabanlar aynı ise üsler toplanır. Bu, üstlerimizden birinin negatif olması durumunda da geçerlidir. Bu durumda aşağıda da görebileceğiniz basit bir işlemle sonucu göstermiş oluruz.
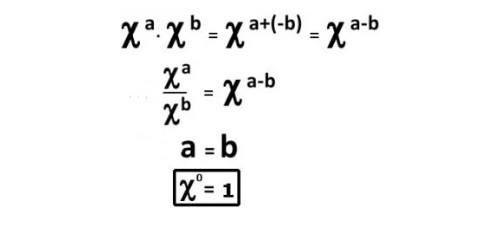
Bir sayının sıfırıncı kuvvetinin neden bir olması gerektiğini açıklarken, yapabileceğimiz ikinci gösterim örüntülerden faydalanmak olacaktır. Desene bakarsanız, üstü bir küçülttüğümüzde sayının değerini 3’e böldüğümüzü düşünebilirsiniz.
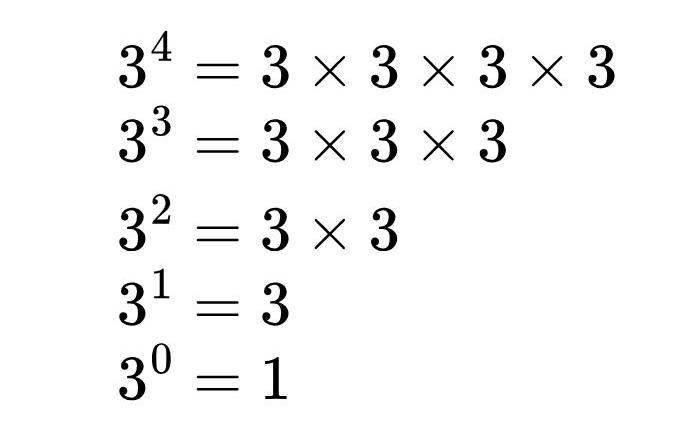
Ancak aslında yaptığımız her seferinde kullandığımız 3 sayısını bir tane azaltmaktır. Arka planındaki mantıkta 1.x=x cebirsel kuralına dayanmaktadır. Şimdi aşağıdaki sayıların hepsinin önünde 1 olduğunu düşünelim. Sonuç aşağıdaki gibi olacaktır.
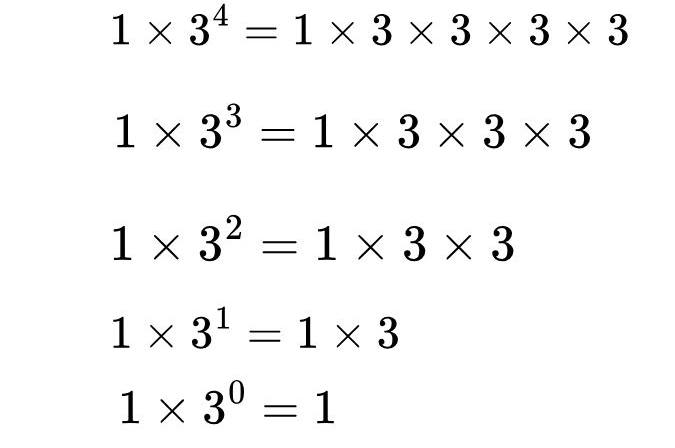
Yukarıdaki açıklamalar temel matematik bilgisine sahip olan bir kişi için yeterlidir. Ancak detaylar hakkında biraz daha kafa yormak isterseniz kategori teorisine giriş yapmanız gerekecektir. Kategori teorisi matematiksel yapılar ve bunlar arasındaki ilişkilerle soyut olarak ilgilenen bir matematik kuramıdır. İşlemleri nesneler ve morfizmler açısından tanımlamak zorundadır.
Teorinin detayları bu yazının kapsamı dışındadır. Ancak merak ederseniz kısaca bu yazıdan detay öğrenebilirsiniz. Bilmeniz gereken şey kategori teorisinde boş çarpımların bir ile gösterildiğidir. ( Matematikte pek çok farklı türde çarpım vardır: Sadece sayıları, polinomları veya matrisleri çarpabilmenin yanı sıra, birçok farklı cebirsel yapıya ilişkin çarpımlar da tanımlanabilir.)
Sıfırın Sıfırıncı Kuvveti Kaçtır?
Şu ana kadar, sıfır dışında, herhangi bir sayının sıfırıncı kuvvetinin neden bir olması gerektiğini açıklamaya çalıştık. Peki, sıfırın sıfırıncı kuvvetini aldığımızda ne olur? Aslında bu sorumuza verebileceğiniz cevap keyfidir.
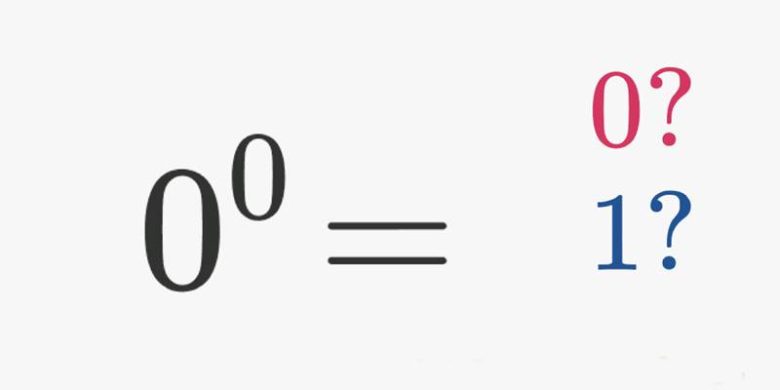
Cebir ve kombinatorikte genellikle sonuç 1 olarak kabul edilmektedir. Matematiksel analizde ifade bazen tanımsız olarak kabul görür. Programcılar da sorunu farklı biçimde ele alırlar. Yani sonuçta sıfırın sıfırıncı kuvvetini kaç kabul edeceğiniz biraz da keyfidir ve matematikçiler arasında ortak bir kabul yoktur.
Kaynaklar ve ileri okumalar:
- Why any number to the zero power always gives a one?; Bağlantı: http://scienceline.ucsb.edu
- The Most Controversial Number in Math. Kaynak site Youtube. Bağlantı: The Most Controversial Number in Math
- Zero Power Rule: Why Is A Number Raised To Power Zero Equal To One?; yayınlanma tarihi: 19 Ekim 2023. Kaynak site: Science ABC. Bağlantı: Zero Power Rule: Why Is A Number Raised To Power Zero Equal To One
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel






