Şimdiye kadar âşık olmuş herkes, size asıl önemli olanın büyük sözler değil, sevilen kişiye dair küçük ayrıntılar olduğunu söyleyecektir. Günlük alışkanlıklar, ufak ritüeller, sadece ikinize özel olan paylaşımlar… Bazı insanlar için ise aşkın nesnesi matematiğin kendisidir. Onlar için sayılar yalnızca hesap yapmanın aracı değildir; kendi içlerinde anlamlı, derinlikli varlıklardır. İşte bu ilişkileri inceleyen matematik dalına Sayılar Teorisi denir.
Sayılar teorisi, şekillerle ya da sürekli niceliklerle değil, doğrudan sayılarla ilgilenen bir matematik dalıdır. Matematikçiler bu alanda, sayılar arasındaki ilişkileri ve özellikleri hem teorik hem de deneysel yaklaşımlarla inceleyerek, sayıların altında yatan yapıları ve kuralları anlamaya çalışır.
Sayılar teorisi yalnızca profesyonel matematikçileri değil, aynı zamanda amatörleri de cezbetmiştir. Çünkü bu alandaki birçok problem ve teorem, diğer matematik dallarına kıyasla daha anlaşılır bir yapıya sahiptir. Sıradan bir kişi bile bazı klasik soruları kavrayacaktır.
Ancak, bu problemleri çözmek, çoğu zaman ileri düzey matematiksel altyapı gerektirir. Yüzeyde basit gibi görünen birçok soru, çözüm aşamasında oldukça derin teknik bilgi talep eder. Bu da sayıların arkasında yatan yapının hem sade hem de son derece güçlü
Sayılar Teorisinde Hangi İlişkiler İncelenir?
Matematik dünyası, her biri kendine özgü özelliklere sahip birçok sayı türü sunar. Matematikçiler, bu sayıların ve sayı kümelerinin birbiriyle nasıl ilişkili olduğunu anlamaya çalışır. Bu ilişkileri açıklamak için teoriler geliştirirler. Bu teoriler, genellikle aksiyomlar (doğru kabul edilen temel önermeler) ve teoremler (diğer teorem ya da aksiyomlara dayalı olarak kanıtlanan ifadeler) ile desteklenir.
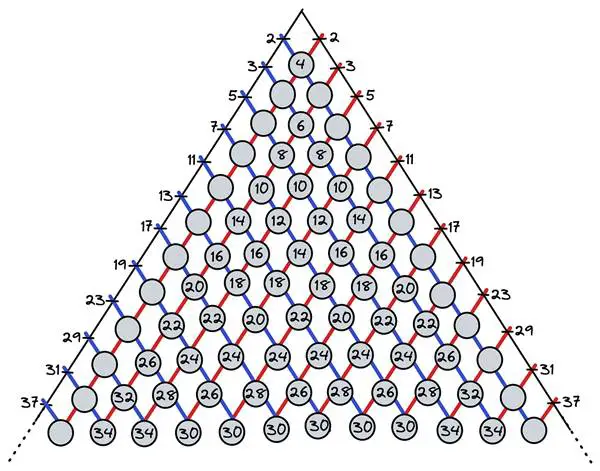
Bu alanın merkezinde, yalnızca 1’e ve kendisine bölünebilen asal sayılar yer alır. Tıpkı biyolojide DNA’nın temel yapı taşı olması gibi, asal sayılar da sayılar teorisinin temelini oluşturur. Asal sayılar üzerine yapılan çalışmalarda önemli bir dönüm noktası, kare karşılıklılık yasası (quadratic reciprocity) ilkesidir. Bu ilke, asal sayılarla ilgili nelerin kanıtlanabileceğine dair matematiksel bakışı köklü biçimde değiştirmiştir.
Eğer asal sayıları bir dağ silsilesi gibi düşünürsek, karşılıklılık ilkesi, daha önce ulaşılamayan zirvelere giden dar ama sağlam bir patika gibidir. Matematikçiler bu zirvelere çıktıkça, daha önce gizli kalmış matematiksel gerçekleri görme şansı elde eder.
Asal Sayı Çiftlerinde Örüntüler: Karşılıklılık ve Modüler Aritmetik
Karşılıklılık (reciprocity) ilkesini anlayabilmek için önce modüler aritmetiği anlamak gerekir. Modüler aritmetik, bir sayının başka bir sayıya bölündüğünde kalanını hesaplamaya dayanır. Bu işlemde kullanılan bölen sayıya modül denir. Örneğin, “9 mod 7 = 2” ifadesi, 9’un 7’ye bölündüğünde kalanın 2 olduğu anlamına gelir. Mod 7 sisteminde, sadece şu 7 sayı bulunur: {0, 1, 2, 3, 4, 5, 6}. Bu sayılarla toplama, çıkarma, çarpma ve bölme işlemleri yapılabilir.
Tıpkı tam sayılarda olduğu gibi, modüler sistemlerde de mükemmel kareler vardır. Mükemmel kare, bir sayının kendisiyle çarpımına eşittir. Örneğin, mod 7 altında 0, 1, 2 ve 4 mükemmel karedir. Çünkü:
- 0 × 0 = 0
- 1 × 1 = 1
- 2 × 2 = 4
- 3 × 3 = 9 ≡ 2 mod 7
- 6 × 6 = 36 ≡ 1 mod 7
Modüler sayı sistemleri sınırlı olduğu için, mükemmel kareler burada daha sık karşımıza çıkar. Kuadratik karşılıklılık (quadratic reciprocity) ise oldukça sade bir sorudan yola çıkar: İki asal sayı p ve q verildiğinde, eğer p sayısı mod q altında bir mükemmel kare ise, q da mod p altında mükemmel kare olur mu?
Cevap, bu asal sayıların 4’e bölümünden kalanlara bağlıdır. Eğer p veya q’dan en az biri 4’e bölündüğünde kalan 1 ise, o zaman bu iki asal sayı karşılıklı davranır: p, mod q altında kare ise, q da mod p altında karedir.
Bu örnekler, asal sayılar arasında görünen basit gibi görünen yapıların aslında nasıl derin, simetrik ve kurallı bir doğaya sahip olduğunu gösterir. Kuadratik karşılıklılık, sayıların gizli düzenini çözmekte matematikçilere kılavuzluk eden güçlü bir ilkedir.
Sayılar Teorisi Nasıl Çalışır?
20. yüzyılın ortalarına kadar sayılar teorisi, gerçek dünyaya doğrudan uygulaması olmayan, matematiğin en saf dalı olarak kabul ediliyordu. Ancak bilgisayarların ve dijital iletişimin ortaya çıkışı, sayılar teorisinin gerçek dünyadaki sorunlara beklenmedik yanıtlar sağlayabileceğini ortaya çıkardı.
Sayılar teorisi, matematiksel ilişkileri analiz etmenin yanı sıra onlar hakkında yeni sorular sormayı da içerir. Örneğin Pisagor teoremini (a2+b2=c2) sağlayan sayılara Pisagor üçlüsü denir. (3,4,5) gibi bu sayı üçlüsü a2+b2=c2 denklemini çözer. Peki ya a3+b3=c3?
Matematikçi Pierre de Fermat da küpler hakkında aynı soruyu sordu. 1650 yılı civarında Fermat Diophantus’un Arithmetica adlı kitabının kenarına gizemli bir not yazdı. “… Cuius rei demonstrationem mirabilem sane detexi. Hanc marginis exiguitas non caperet!”. Bu şunun gibi bir anlama gelmekteydi. “Teoremin müthiş bir kanıtını buldum fakat burada yazacak kadar yer yok”.
Fermat meşhur notunu tam da Pisagor üçlüleri ile ilgili kısmın yanına yazmıştı. O zamandan sonra bu kitabı okuyan matematikçiler Fermat’ın iddialı sözüyle karşılaşınca hadi bizde deneyelim diye işe giriştiler. Sonunda Fermat’a meydan okuma yarışı başladı.
Aslında Fermat kitabın kenarlarına ispatı verilmemiş sayılar kuramı ile ilgili başka sorular da yazmıştı. Süreç içinde matematikçiler diğer tüm problemleri ispat ettiler. Sonunda geriye doğruluğu ya da yanlışlığı ispatlanamayan son bir teorem kaldı. Bu nedenle doğal olarak bu teorem Fermat’ın son teoremi olarak bilinmeye başlandı. 1635-1637 arasında ileri sürülen bu teorem ancak 1994 yılında İngiliz matematikçi Andrew Wiles tarafından kanıtlandı. Bu sayılar teorisinin nasıl çalıştığının güzel bir örneğidir.
Sayılar Teorisi Çözümsüz Problemlerle İle Doludur
Bugüne kadar kazanılmış onlarca zafere rağmen, sayılar teorisi halen birçok çözülmemiş sorunun kaynağıdır. Üstelik en kafa karıştırıcı olanlardan bazıları da oldukça masum görünmektedir. Örneğin, “Tek mükemmel sayılar var mı?” bilmiyoruz. “Sonsuz sayıda ikiz asal var mıdır?” ya da “Goldbach’ın varsayımı doğru mu?” bunları da bilmiyoruz. Bu nedenle günümüzde hala pek çok sayı teorisyeni bu sorulara hala cevap arıyor. Sayılar teorisi ve çeşitli alt alanları matematik severlerin aklını daha uzun süre meşgul edecek gibi gözüküyor.
Kaynaklar ve ileri okumalar
- What Is Number Theory? Bağlantı: http://science.howstuffworks.com
- Duke, William & Spears, Kimberly. (2003). Quadratic Reciprocity in a Finite Group. The American Mathematical Monthly. 112. 10.2307/30037441.
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel