Bazen matematik öylesine zarif ve etkileyici bir şekilde karşımıza çıkar ki, insan bunu kendi keşfetmemiş olsa bile “Eureka!” diye haykırmak ister. Genellikle bu his, alışılmadık bir bakış açısı, beklenmedik bir bağlantı veya sorunun yeni bir şekilde ele alınmasıyla karmaşık bir şeyin aniden basit görünmesiyle ortaya çıkar. Bu tür şaşırtıcı matematiksel yaklaşımların en güzel örneklerinden biri, Sanat Galerisi Problemi olarak bilinen sorudur.

Matematikçi Victor Klee tarafından 1973 yılında ortaya atılan bu problem, geometrik hesaplamalarla ilgilidir ve sanal bir sanat galerisini en az kaç güvenlik kamerasının kapsayacağını bulmaya çalışır. Yaklaşık beş yıl sonra, matematikçi S. Fisk, bu problemi ele almak için oldukça zarif bir yöntem geliştirdi.
İlginç olan, bu problem daha önce Václav Chvátal tarafından farklı bir yöntemle ispatlanmış olmasına rağmen, Fisk’in çözümü beklenmedik derecede şık ve sezgisel bir yaklaşım sundu. Öyleyse, bu problemin ne anlama geldiğini anlamak için önce temel fikri ortaya koyalım.
Sanat Galerisi Problemi Nedir?
Bir sanat galeriniz olduğunu ve burada paha biçilmez tablolar ve heykeller sergilendiğini düşünelim. Galerinin tamamını güvenlik altına almak için belirli noktalara güvenlik görevlileri yerleştirmek istiyorsunuz. Peki, galeriye en az kaç güvenlik görevlisi yerleştirmeniz gerekir ki her noktayı gözlemleyebilsinler?
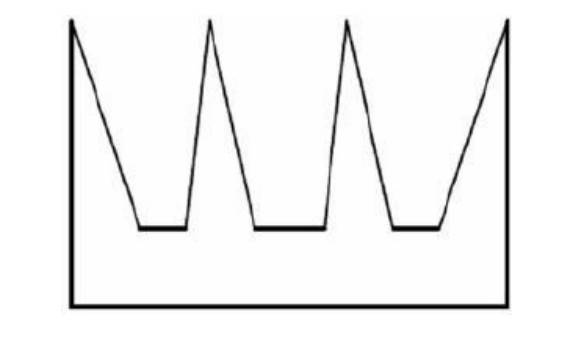
Gerçek hayatta çoğu bina dikdörtgen olsa da, sanat galerileri sıra dışı tasarımlara sahip olur. Bu yüzden, genel bir çözüm bulmak zorlaşır. Ancak problemi daha yönetilebilir hale getirmek için, galerinin basit bir çokgen olduğunu varsayacağız. Yani kenarları doğrusal olacak, birbirini kesmeyecek ve içinde delik ya da boşluk bulunmayacak. Ayrıca, güvenlik görevlilerinin hareket etmediğini ve yalnızca çokgenin köşelerine yerleştirildiğini kabul edeceğiz.
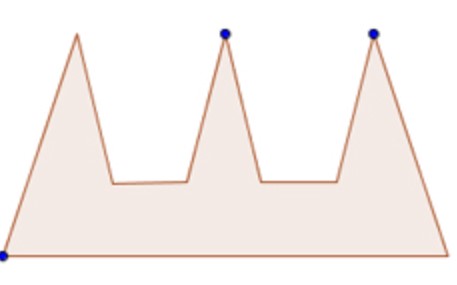
İlk bakışta, gerekli güvenlik görevlisi sayısının çokgenin köşe sayısına bağlı olduğu sezgisel olarak açıktır. Çünkü daha fazla köşeye sahip bir galeri, görüş alanı kısıtlı olan dar girintilere sahip olacaktır. Şimdi, n ile çokgenin köşe sayısını ifade edersek (örneğin, burada n = 9), matematikçi S. Fisk‘in ortaya koyduğu zekice bir yaklaşım, herhangi bir basit çokgeni korumak için en fazla n/3 güvenlik görevlisinin yeterli olduğunu gösterir.
Bu durumda, 9 köşeli bir galeri için 9/3 = 3 güvenlik görevlisi yeterlidir. Bu sonuç, çokgenin ne kadar karmaşık ve düzensiz göründüğünden bağımsız olarak geçerlidir. Yani, herhangi bir basit çokgenin tamamını kapsamak için gereken güvenlik görevlisi sayısı, köşe sayısının üçte birini asla geçmez. Bu güçlü ve genel geçer sonuç, Sanat Galerisi Problemi’ni çözmede önemli bir dönüm noktasıdır.
Sanat Galerisi Probleminin Çözümü Nedir?
Bir güvenlik görevlisi, galeri içindeki belirli bir p noktasını yalnızca aralarında herhangi bir duvar yoksa görecektir.. Eğer galeriyi böyle koşulları sağlayan bölgelere ayırabilirsek, her bir bölgeyi yalnızca bir köşeye yerleştirilen bir güvenlik görevlisinin görebileceğini garanti edebiliriz. Bu da galerinin tamamını kapsayan optimal bir güvenlik yerleşimi oluşturduğumuz anlamına gelir.
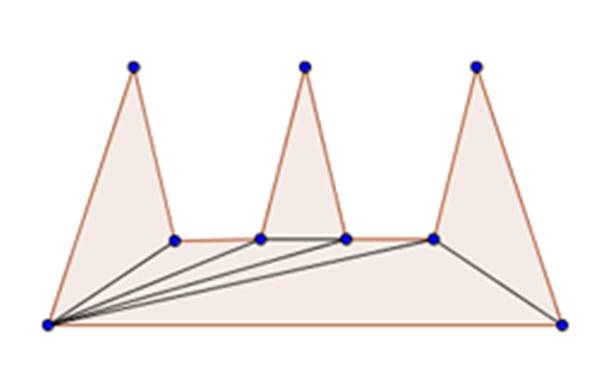
Bu tür bir bölgeleme yapmanın en etkili yöntemlerinden biri, çokgeni üçgenlere ayırmaktır. Üçgenleme (triangulation) adı verilen bu teknik, çokgenin köşelerini düz çizgilerle birbirine bağlayarak onu üçgenlere bölmeyi içerir.
Bir güvenlik görevlisini üçgenin bir köşesine yerleştirdiğimizde, o güvenlik görevlisi üçgenin tamamını görecektir. Bunun nedeni, üçgenin konveks bir şekil olmasıdır. Yani, üçgen içindeki herhangi iki noktayı birleştiren doğru parçası, üçgenin dışına taşmaz ve tamamen içinde kalır.
Şu anda baktığımız şekil, üçgenlere bölünmüş bir çokgendir. Ancak bunu farklı bir şekilde de düşünebiliriz. Bu şekil, matematikçilerin graf olarak adlandırdığı bir yapıdır. Grafik kuramcıları, graf üzerindeki köşelerin veya kenarların belirli kurallara göre renklendirilmesiyle ilgili problemleri çözmeyi severler. Fisk’in dahice buluşu, güvenlik görevlisi yerleştirme problemini böyle bir renklendirme problemine dönüştürmek oldu.
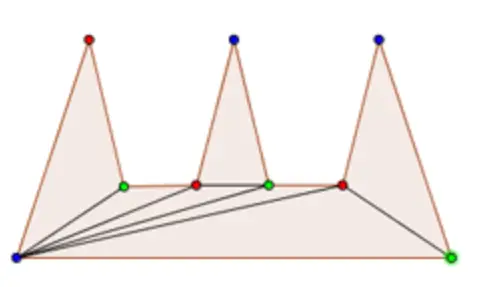
Üç farklı renk kullanarak köşeleri boyamayı deneyelim ve her üçgenin üç köşesinin de farklı renklere sahip olmasını sağlayalım. Daha sonra belirli bir rengi, örneğin maviyi seçelim. Bu renge boyanmış olan her köşeye bir güvenlik görevlisi yerleştirelim. Her üçgende tam olarak bir mavi köşe olacaktır. O nedenle, bu yöntem her üçgenin en az bir güvenlik görevlisi tarafından görülmesini garanti eder.
Peki, bu yerleşim kaç güvenlik görevlisi gerektirir? Renklendirme işlemi, köşeleri üç farklı gruba ayırır; her biri farklı bir rengi temsil eder. Amacımız güvenlik görevlisi sayısını en aza indirmek olduğundan, en küçük grubu seçmekle ilgileniyoruz. Biraz düşünerek, bu en küçük grubun hiçbir zaman n/3’ten fazla köşe içermeyeceğini fark edebiliriz. Ve işte, Fisk’in çözümüne ulaştık!
Sonuç Olarak;
Sanat Galerisi Problemi’nin bir diğer ilginç yanı, yeni keşifler için pek çok farklı yol sunmasıdır. Peki ya güvenlik görevlileri yalnızca galerinin köşelerinde durmak zorunda olmasa? Hareket edebilmelerine izin verilirse ne olurdu? Ya galerinin ortasında görüşü engelleyen engel veya sütunlar olsaydı? Eğri duvarlara sahip bir galeri için çözüm nasıl değişirdi?
Bunun ötesinde, iki boyutlu bir çokgeni korumak yerine üç boyutlu bir çokyüzlü korumaya çalışsaydık ne olurdu? Hatta, bir sanat galerisi yerine, bir hapishanenin dışındaki güvenlik görevlilerinin duvarları gözetlediği bir senaryoyu ele alsaydık?
Matematikçiler, bu soruların bazılarının yanıtlarını bulmuşlardır. ancak bazı ispatlar oldukça zorlayıcı olmuştur. Yine de keşfedilecek çok şey var ve bu alanda daha pek çok zarif matematiksel çözümün ortaya çıkmasını heyecanla bekliyoruz.
Kaynaklar ve İleri Okumalar:
- The art gallery problem; yayınlanma tarihi: 14 Temmuz 2014; Kaynak site: Plus Math. Bağlantı: The art gallery problem
- AFragkoudakis, Christodoulos & Markou, Euripides & Zachos, Stathis. (2005). How to Place Efficiently Guards and Paintings in an Art Gallery. 3746. 145-154. 10.1007/11573036_14.
- John D. Barrow; 100 Essential Things You Didn’t Know You Didn’t Know about Math and the Arts. ISBN: 0393352226
- Couto, Marcelo & Souza, Cid & De Rezende, Pedro. (2007). An Exact and Efficient Algorithm for the Orthogonal Art Gallery Problem. Proceedings of SIBGRAPI 2007 – 20th Brazilian Symposium on Computer Graphics and Image Processing. 87 – 94. 10.1109/SIBGRAPI.2007.15.
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel