Leonardo da Vinci, “Matematiksel olarak gösterilemeyen hiçbir araştırma gerçek bilim sayılamaz.” sözü ile anımsanır. Bu söz günümüzde daha da doğrudur: Her araştırma matematiği içerir. Peki ama tam olarak hangi matematik? Bu yazıda konuya yabancı olanlar için saf matematik ile uygulamalı matematik farkını ele alacağız.

Genel olarak konuşursak, iki farklı matematik türü vardır. Bunlar saf ve uygulamalı matematik. Saf ve uygulamalı mutlaka birbirini dışlayan şeyler değildir. Her iki alanda da çalışan birçok büyük matematikçi vardır. Ancak matematiğin temelleri saf matematikten gelir.
Uygulamalı Matematik Nedir?
Uygulamalı matematikçiler matematiğin gerçek dünyadaki kullanımlarına odaklanırlar. Mühendislik, ekonomi, fizik, finans, biyoloji, astronomi; tüm bu alanların soruları yanıtlamak ve sorunları çözmek için matematiksel tekniklere ihtiyacı vardır.
Uygulamalı matematikçiler genellikle fiziksel dünyadan kaynaklanan problemlerle uğraşırlar. Bunu yapmak için, gerçek dünyada karşılaşılan durumu, matematiksel dilde açıklamak gerekecektir. Bir durumu matematiksel bir gösterime dönüştürme eylemine modelleme denir.

Bu süreç çok fazla yaratıcılık ve eldeki problemin anlaşılmasını gerektirir. Uygulamalı matematikçiler, kullanışlı olacak kadar gerçekçi ve uygulanabilecek kadar basit modeller arasında bir denge bulmak zorundadır. Kimi durumda, bu modelleri oluşturmak birkaç yıl sürer. Bu süreçte uygulamalı matematikçiler çoğu zaman diğer disiplinlerdeki bilim insanlarıyla ortaklaşa çalışma yapmak zorunda kalırlar.
Bir durumu temsil eden matematiksel bir problem yazıldıktan sonra, modelleme sürecindeki ikinci adım problemi çözmektir. Mevcut tüm matematik burada devreye girer ve saf matematik alanları, matematiğin gerçek dünyaya uygulanmasından kaynaklanan karmaşık matematik problemlerini çözmek için kullanılır. tüm matematik burada devreye girer.
Modelleme sürecinin üçüncü adımı matematiksel çözümün uygulanan problemin çözümüne dönüştürülmesi olacaktır. Uygulamalı matematik böyle çalışır.
Kanıt matematiğin özüdür. Herhangi bir matematiksel sonuç, belli bir mantıksal akıl yürütme zinciri kullanılarak ilk ilkelerden türetilmelidir. Kanıt, matematiği diğer entelektüel çabalardan ayıran şeydir. Bu fikir de bizi saf matematiğe götürecektir.
Saf Matematik Nedir?
Saf matematik uygulamalarla ilgili değildir. Gerçek dünya sorunları ile de ilgili değildir. Saf matematik kalıplar, fikirler ile ilgilidir. En basit ifadeyle, matematik için matematiktir. Soyut kavramları, karmaşık teorileri ve daha önce çözülmemiş sorunları araştırır.
Örneğin “Sonsuz sayıda ikiz asal sayı var mıdır?” gibilerinden soruların yanıtlarını bulmaya çalışırlar. Buldukları yanıtların gerçek dünyada bir karşılığının olup olmaması ile de ilgilenmezler.

Bu nedenle saf matematik büyük ölçüde akademik bir çabadır. Saf matematikçiler birbirlerinin hipotezlerini test eder ve matematik ile ilgili henüz keşfedilmemiş konularla ilgili çalışmalar yürütürler. Bunu yaparken saf matematikçilerin hiçbir hedefi yoktur. Ancak bu kesinlikle saf matematik bir işe yaramaz anlamına da gelmemelidir.
Saf matematikte, ilk başlarda işe yaramaz gibi görünen ancak yıllar sonra önemli uygulamalara sahip olan birçok tarihsel keşif örneği vardır. Ancak çığır açan bir denklem veya formülün arkasındaki orijinal amaç nadiren “yararlılık”tır.
Saf matematikçiler, keşfedilmemiş bir bölgenin haritasını tamamlamaya çalışan kaşifler gibidir. Uygulamalı matematikçiler ise saf matematikçiler tarafından yapılan çizelgeleri ve haritaları kullanan denizcilere benzerler. Her ikisinin de bilimin ilerlemesinde önemli rolleri vardır. Ancak uygulamalı matematik gücünü saf matematikten alacaktır.

Saf Matematik Neden Önemlidir?
Çözülmemiş uygulamalı matematik problemlerine yaklaşırken, uygulamalı ve saf matematik arasındaki ayrım sıklıkla ortadan kalkar. Bir zamanlar çok soyut olarak kabul edilen alanlar, modern problemler için tam olarak ihtiyaç duyulan şeyler olmuştur.
Yaklaşık 2000 yıl boyunca matematikçiler beşinci Öklid aksiyomunu diğer dört aksiyomdan çıkarmaya çalıştılar. 1830’da Lobachevski ve Bolyai beşinci aksiyomun bağımsızlığını kanıtladılar. Bu devrim niteliğinde bir keşifti ama Einstein bunu genel görelilik teorisinde uygulayana kadar kimseye bir faydası yoktu yani tamamen teorikti.
Geçmişte sayılar teorisi işe yaramaz matematiğin bir örneği olarak görülüyordu. Yıllar sonra sayı teorisinin sonuçları, özellikle asal sayılar teorisi, bilgisayar güvenlik sistemlerinin tasarımında uygulandı. Bu sayede çevrimiçi rezervasyon, alışveriş veya bankacılık işlemleri yaptığımızda matematik tarafından korunuruz.
Kullandığımız Bilgisayarları Saf Matematiğe Borçluyuz

Entscheidungs problemi 1928’de ünlü matematikçi David Hilbert tarafından formüle edildi. Problem, girdi olarak bir ifadeyi dikkate alan ve ifadenin evrensel olarak geçerli olup olmadığına göre “evet” veya “hayır” yanıtını veren bir algoritma olup olmadığını sorar.
Bu soruyu birbirinden bağımsız olarak, 1936 ve 1937’de Alonzo Church ve Alan Turing yanıtladı. Makalesinde Turing, günümüzde Turing makinesi adını verdiğimiz soyut bir makine formüle etti.
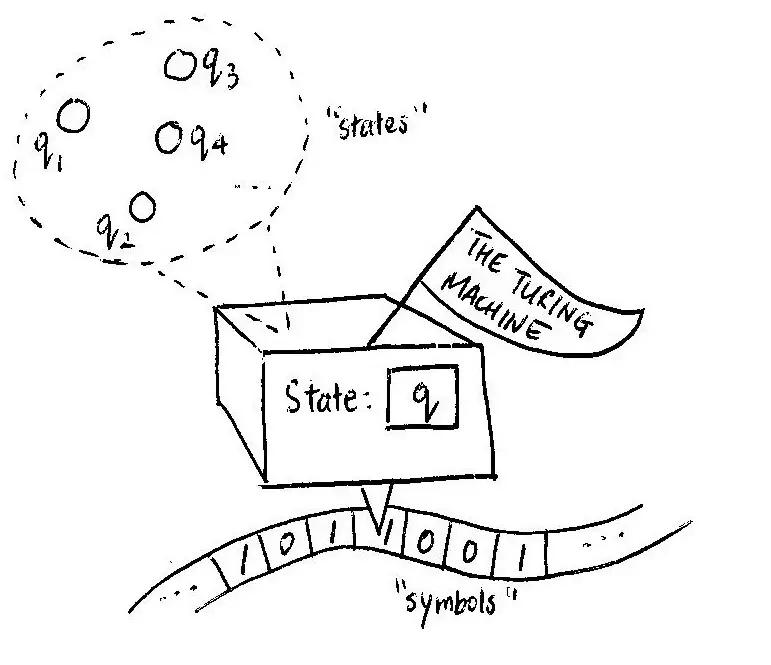
Turing makinesi aritmetik hesaplamalarının kağıt kalem ile yapılma sürecini taklit eden hayali bir cihazdı. Makinenin sonsuz uzunlukta bir bandı (belleği), her seferinde adım adım hareket edebilen, banttan okuyup yazabilen bir kafası, kafaya talimatlar veren sonlu bir talimat tablosu ve sonlu bir dizi durumu vardı.
Böyle bir makine sonsuz uzunlukta bir banda sahip olduğundan matematik dışında var olamaz. Gerçek bir bilgisayar tarafından yapılabilecek herhangi bir hesap Turing makineleriyle de yapılabilir. En temel fark, gerçek bilgisayarların aksine, Turing makinelerinin okuyabileceği, işleyebileceği ve yazabileceği veri miktarının sınırsız olmasıdır.
Matematikçinin fiziksel dünyanın sınırlamaları tarafından kısıtlanmaması ve soyut nesneler yaratmak ve inşa etmek için hayal gücüne başvurabilmesi belki de saf matematiğin bir özelliğidir. Matematiğin temelleriyle ilgili soyut bir problemin, modern bilgisayarın ortaya çıkışının temellerini atması da dikkat çekicidir.
Sonuç olarak
Dönem dönem belli matematiksel keşifler karşısında, iyi de bu ne işe yarayacak biçiminde soru bir çok kişinin aklına gelir. Ancak bir saf matematikçi buluşunun işe yarayıp yaramaması ile ilgilenmez. Onun asıl ilgisini çeken şey keşfetme sürecidir.
Matematiği kendi kullanabilen herkes bir nevi uygulamalı matematikçidir. Öte yandan, saf matematikçiler, “imkansız” gibi görünen problemleri çözmek için yıllarını harcayacaklardır. Onlar “denizin kaşifleridir” ve onlar olmadan matematik asla ilerlemeyecektir.
Kaynaklar ve ileri okumalar
- Explainer: the point of pure mathematics. Yayınlanma tarihi: 1 Ağustos 2011. Kaynak site: Conversation. Bağlantı: Explainer: the point of pure mathematics
- Kachapova, Farida. (2014). On the Importance of Pure Mathematics. Journal of Mathematics and Statistics. 10. 421-422. 10.3844/jmssp.2014.421.422.
- Andersen, Kirsti & Bos, Henk. (2006). Pure Mathematics. The Cambridge History of Science: Early Modern Science. 3. 10.1017/CHOL9780521572446.029.
- Want to solve a complex problem? Applied math can help. Yayınlanma tarihi: 1 Kasım 2024. Kaynak site: Conversation. Bağlantı: Want to solve a complex problem? Applied math can help
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel