Sevin ya da sevmeyin, Rubik Küpü — ülkemizde bilinen adıyla zeka küpü — dünyanın en popüler bulmacalarından biridir. İlk olarak 1974’te Macar heykeltıraş ve mimar Ernö Rubik tarafından Sihirli Küp adıyla tasarlanan bu oyuncak, 1980’ler ve 90’ların başında dünya genelinde milyonlarca kişinin ilgisini çekmiştir.

Rubik Küpünü çözmekte zorlanıyorsanız endişelenmeyin; yalnız değilsiniz. Mucidi Ernö Rubik’in bile kendi icadını çözmesi bir ayını almıştı. Bunun nedeni, standart bir 3×3 Rubik Küpünün 43 kentilyondan fazla olası kombinasyona sahip olmasıdır. Ancak bu devasa sayı içinde yalnızca bir doğru çözüm vardır.
Küpten rastgele hamlelerle doğru sonuca ulaşmak neredeyse imkânsızdır. Bunun yerine, belirli çözüm stratejilerini öğrenmek süreci hem hızlandırır hem de çok daha keyifli hale getirir.

Rubik Küpü En Hızlı Çözme Rekoru Kime Aittir?
Rubik Küpü’nü en hızlı çözme rekoru, sürekli olarak gelişen bir alandır ve “Speedcubing” adı verilen bu spor dalı, dünya genelinde binlerce kişiyi bir araya getirir. Şu anda 3×3 Rubik Küpü çözme dünya rekoru, Yusheng Du adlı Çinli bir oyuncuya aittir. Yusheng Du, bu rekoru 3.47 saniyede çözerek 2018 yılında kırmıştır.
Bu olağanüstü başarı; modern çözüm teknikleri, hızlı el becerisi ve gelişmiş algoritma bilgisi sayesinde mümkün oldu. Du’nun kullandığı yöntem, Dr. Jessica Fridrich tarafından geliştirilen ve turnuvalarda en etkili çözümlerden biri olarak bilinen Fridrich yöntemiydi.

Rubik Küpü’nü Tanıyalım
Rubik Küpü’nü çözmeye başlamadan önce, onu yakından tanımak gerekir. Standart bir Rubik Küpü, her biri büyük küpün üçte biri boyutunda olan 27 küçük küpten oluşur. Bu küçük parçalar, küpün altı farklı renkten oluşan yüzeylerini meydana getirir.
Her yüzün tam ortasında bir merkez parça bulunur. Bu merkezler, küpü bir arada tutan çekirdek yapıya bağlıdır ve asla yer değiştirmez. Dolayısıyla, merkez parça o yüzün ana rengini belirler. Küpü ilk elinize aldığınızda, her yüz tek renkten oluşur. Amacınız, küpü milyonlarca olası kombinasyondan birine karıştırmak ve ardından bu karışıklığı çözerek başlangıçtaki düzenine geri getirmektir.

Rubik Küpü’nün hareketli parçaları iki ana gruba ayrılır: köşe küpleri ve kenar küpleri. Bu parçaların konumunu ve işlevini bilmek, çözüm sürecinin temel adımlarından biridir.
Küp üzerinde 12 adet kenar küpü bulunur. Bu parçalar, iki farklı renkten oluşur ve küpün her bir kenarında yer alır. Kenar küplerini doğru konumlandırmak, küpün tamamlanması için kritik öneme sahiptir.
Küpün merkezinde ise sabit merkez küpler yer alır. Bu parçalar tek renklidir ve bulundukları yüzün ana rengini belirler. Standart bir Rubik Küpü’nde renklerin karşılıklı yerleşimi şu şekildedir: beyaz-sarı, kırmızı-turuncu, mavi-yeşil.
Rubik Küpü Matematik Açısından Neden Önemlidir?
Rubik Küpü, matematiğin soyut dünyasını somut bir bulmacaya dönüştüren keyifli bir oyundur. Onu bu kadar ilginç ve karmaşık yapan, üç eksende de döndürülebilmesidir. Bu özelliği sayesinde, standart bir 3x3x3 Rubik Küpü, 43.252.003.274.489.856.000 farklı kombinasyona sahiptir. Bu sayı (3 8 x 8!)(2 12 x 12!)/12 biçimindedir.
Rubik Küpü’nde 8 köşe ve 12 kenar küp bulunur. Köşe küpler 3 yönde döner ve 8! farklı şekilde dizilir. Kenar küpler ise 2 yönde döner ve 12! farklı şekilde dizilir. Bu olasılıkları çarptığımızda 519 kentilyon farklı düzen ortaya çıkar. Ancak bunların yalnızca 1/12’si fiziksel olarak mümkündür. Bu da toplamda 43 kentilyon farklı kombinasyon demektir.
3×3’lük Bir Rubik Küp Nasıl Çözülür?
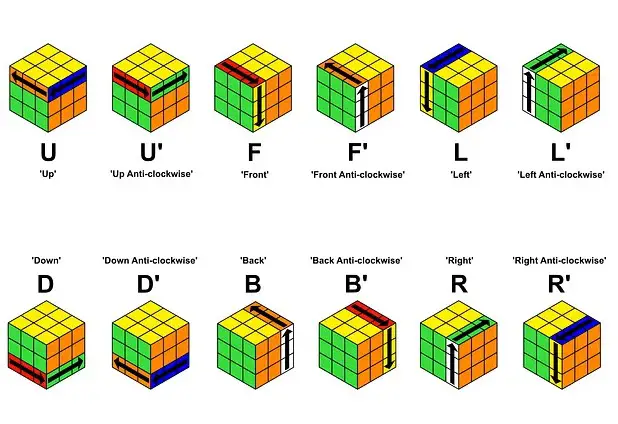
Rubik Küp’ün tek tek renkleri bitirerek çözüldüğü düşüncesi yaygın bir yanılgıdır. Küpün yapısı ve parçalarının çalışma prensibi nedeniyle bu mümkün değildir. Bunun yerine, küp katman katman çözülür. Rubik Küp çözümünde kullanılan kısaltmalar aşağıdaki gibidir.
- R → Sağ taraf yukarıya doğru
- R’ → Sağ taraf aşağıya doğru
- L → Sol taraf aşağıya doğru
- L’ → Sol taraf yukarıya doğru
- F → Ön yüz saat yönünde
- F’ → Ön yüz saat yönünün tersi
- U → Üst yüz saat yönünde
- U’ → Üst yüz saat yönünün tersi
1. Adım: İlk Katman – Beyaz Artı
Başlangıç katmanı olarak beyaz yüz seçelim. Beyaz artıyı oluşturmak için şu adımları izleyin:
- Beyaz kenar parçasını bulun. Bir kenar parçası iki renkten oluşur. Beyaz kenar parçası, bir yüzünde beyaz, diğer yüzünde farklı bir renk barındırır.
- Beyaz olmayan kısmı, kendi merkez rengiyle eşleştirin. Bu işlemi genellikle 2-3 hamlede kolayca yapabilirsiniz.
- Beyaz kısmı beyaz merkezle hizalayın.
- Aynı işlemi diğer beyaz kenar parçaları için tekrarlayın.
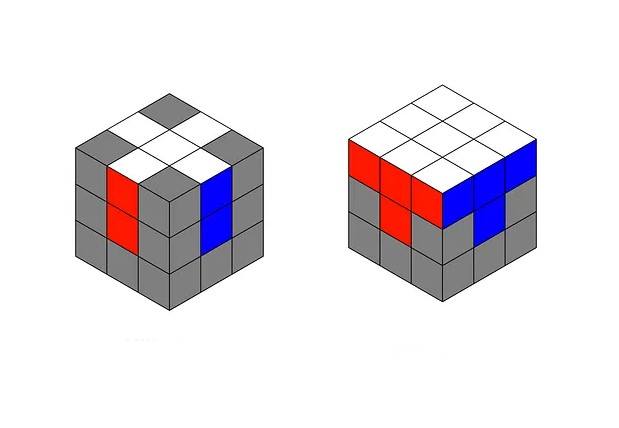
Beyaz artı şekli ve ilk katman tamamlandıktan sonra sıradaki adım, köşe parçalarını doğru konumlarına yerleştirmektir. Bu köşeler, hem üst katmandaki beyaz yüzü tamamlamalı hem de yan yüzlerde renklerin bir şerit şeklinde doğru şekilde devam etmesini sağlamalıdır.
Bu aşama, Rubik Küp’ü ilk kez çözmeye çalışanların en çok hata yaptığı noktadır. Köşeler yanlış yerlere yerleştirildiğinde, küpün geri kalanını çözmek imkânsız hâle gelir
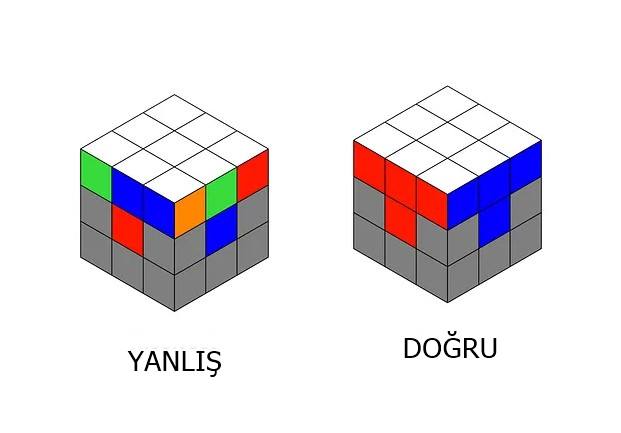
2. Adım: Orta Katman Çözümü
Rubik Küp çözümünde bir sonraki adım, küpü ters çevirmek ve beyaz yüzü alta yerleştirmektir. Bu pozisyondan, orta katmanı çözmeye odaklanacaksınız. Bunun için, kalan sekiz kenar parçasından dördünü doğru konumlarına yerleştirmeniz gerekir. Bu adımı tamamladığınızda, küpün üçte ikisi çözülmüş olacaktır.
İkinci katmanda, sarı olmayan kenar parçalarının doğru konumlara yerleştirilmesi hedeflenir. Bunun için önce sarı olmayan bir kenar parçası bulun ve kenarın sarı olmayan kısmını, aynı renkteki merkezle hizalayana kadar üst katmanı çevirin. Ancak, kenarın diğer yüzü sarı merkeze bağlıdır. Bu renge karşılık gelen merkezi bulun. Bu noktadan sonra da merkezin yönüne göre bir algoritma kullanın.
- Sağa Taşıma Algoritması: U R U’ R’ U’ F’ U F
- Sola Taşıma Algoritması: U’ L’ U L U F U’ F’
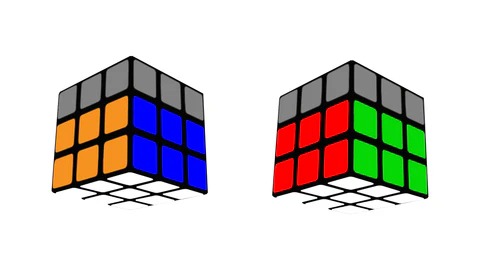
3. Adım: Sarı Artı ve Sarı Yüzün Çözümü
Rubik Küpü’nün üçüncü adımı, sarı yüzü çözmektir. Sarı yüzü çözmeye başlamak için ilk hedefiniz sarı artıyı oluşturmaktır. Sarı artıyı oluştururken üç farklı durumla karşılaşabilirsiniz. Her durumda aynı algoritma işe yarar; ancak başlangıç pozisyonu farklıdır.

Küpü elinize alın ve sarı merkezi yukarı bakacak şekilde yerleştirin. Sonrasında da F R U R’ U’ F’ algoritmasını uygulayın. Bu algoritmayı bir veya iki kez tekrarladığınızda sarı yüzde bir artı şekli oluşacaktır.
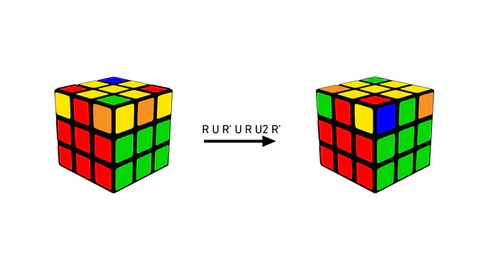
Son katmandaki kenarları merkezleriyle hizalamak için önce üst katmanda herhangi bir kenarı bulun ve orta katmandaki aynı renkteki merkezle eşleştirin. Ardından şu algoritmayı uygulayın: R U R’ U R U2 R’. Tüm kenarlar doğru merkeze gelene kadar aynı algoritmayı tekrarlayın.
Son katmandaki köşeleri eşleştirmek için ise şu algoritma kullanılmalıdır: U R U’ L’ U R’ U’ L. Önce doğru konumda olan bir köşe bulun ve küpü bu köşe sağ ön köşede olacak şekilde tutun. Eğer hiçbir köşe doğru konumda değilse, üstteki eşleşmemiş köşeler yukarıda olacak şekilde küpü istediğiniz pozisyonda tutarak algoritmayı uygulayın.

Üst katmandaki köşelerin yönünü düzeltmek için ise R’ D’ R D algoritmasını kullanın. Sarı yüz yukarı bakarken, düzeltilmemiş köşe sağ ön köşede olacak şekilde küpü tutun. Bu köşe doğru hizalanana kadar algoritmayı tekrarlayın. Ardından üst katmanı çevirerek diğer düzeltilmemiş köşeyi sağ ön köşeye getirin ve aynı algoritmayı uygulayın. Tüm köşeler doğru hizalanana kadar bu işlemi sürdürün.
Rubik Küpü ve “Tanrı’nın Sayısı”

Bazı insanlar Rubik Küp’te hız ve el becerilerini geliştirmeye odaklanırken, bazıları ise küpün en önemli matematik sorusunu merak etti. Küp ne kadar karışık olursa olsun, onu çözmek için gereken en az hamle sayısı nedir? Örneğin, biri küpünüzü 500 hamlede karıştırmış ise, çözmek için 500’den çok daha az hamle yeterlidir. Peki ama bu sayı en az kaçtır?
Bu soru, Rubik Küp’ün matematikteki zirve noktası haline geldi. Acaba öyle bir “sihirli sayı” var mı ki, her karışık küp en fazla bu kadar hamlede çözülebilsin? Erken dönem esprilerde, bu sayının bulunabilmesi için adeta “ilahi yardım” gerektiği söylenirdi. İşte bu nedenle, bu sayıya “Tanrı Sayısı” (God’s Number) dendi.
Tanrı Sayısı üzerine ilk önemli keşif, 1981’de Dr. Morwen Thistlethwaite tarafından yapıldı. Thistlethwaite, küpün en fazla 52 hamlede çözülebileceğini kanıtladı.
1990’lar ve 2000’ler boyunca çalışmalar hız kesmeden sürdü. Sonunda, Haziran 2010’da dört bilim insanından oluşan bir ekip, Tanrı Sayısı’nın 20 olduğunu kesin olarak ortaya koydu. Ancak 43.252.003.274.489.856.000 olası küp konfigürasyonunun tam olarak kaçının gerçekten 20 hamle gerektirdiği hâlâ bilinmiyor.
Öte yandan, yalnızca tek hamle ile çözülecek konumların sayısı 18’dir. Bunun hesaplanması kolaydır. Altı yüz vardır ve her yüz üç farklı şekilde döndürülür. Ancak hamle sayısı arttıkça hesaplamalar giderek karmaşıklaşır.
Sonuç Olarak
Bugünkü bilgilerimiz, 15 hamle uzaklıktaki konumların kesin sayılarını bilmemizi sağlıyor. Ancak 16 ile 20 hamle arasındaki konumların tam sayıları hâlâ kesin olarak bilinmiyor. Rubik Küp ile ilgili son büyük matematik sorusu da işte budur.
Kaynaklar ve ileri okumalar için:
- The Amazing Math Inside the Rubik’s Cube; Yayınlanma tarihi: 4 Ekim 2022; Kaynak site: Popular Mechanics. Bağlantı: The Amazing Math Inside the Rubik’s Cube
- How hard is the Rubik’s cube? Yayınlanma tarihi: 4 Temmuz 2011; Kaynak site: Plus Maths. Bağlantı: How hard is the Rubik’s cube?
Matematiksel





