
Temellerini antik Yunanda atan geometri bilim ve felsefeden siyaset ve sanata kadar yüzyıllar boyunca insan düşüncesine etki etmişti. Ancak 19. yüzyılın başlarında geometrik bir devrim yaşandı. İnsanlar, uzayın tam olarak Öklid’inin ima ettiği gibi olması gerekmediğini anladılar. Bu uyanışın nasıl gerçekleştiğini anlamanız için şimdi sizinle bir deney yapalım.

Bir L doğrusu ve bu doğrunun üzerinde olmayan bir P noktası alalım. P’den geçen,L’ye paralel kaç tane doğru çizebiliriz? Sezgilerimiz bize P’den geçip de L’yi hiç kesmeyecek şekilde yalnızca bir tane doğru çizebileceğini söyler. Nitekim İskenderiyeli Öklid de böyle düşünmüş ve kitabında bunu beşinci postulat olarak belirlemişti.
Ne var ki sezgilerimiz bazen güvenilir bir yol gösterici olmaktan uzaktır. 19. yüzyıl düşünürlerinin devrimci bulduğu şey, uzayın Öklid ve sezgimizin öne sürdüğü gibi olmak zorunda olmadığı, başka türlü de olabileceği gerçeğinin farkına varmalarıydı.
Bu gerçeği keşfedenlerden biri olan Carl-Friedrich Gauss, bu konudaki çalışmasını yayınlamaya cesaret bile edemedi. Ancak matematikçi Bernhard Riemann’ın (diğerlerinin yanı sıra) gösterdiği gibi aslında Öklid dışı birçok uzay vardı.

Nitekim, 1854 yılında Bernhard Riemann tarafından tanıtılan Eliptik geometri diğer adıyla Riemann geometrisi beşinci postulatı geçersiz kılmıştı. Riemann’ın Öklid dışı geometrisi, Albert Einstein’ın genel görelilik kuramını formüle etmek için ihtiyaç duyduğu şeydi.
Riemann Geometrisi Nedir?
Öklid Geometrisi, düzlem ile ilgilidir. Okullarda öğrendiğimiz geometri ile ilgili tüm kavramlar Öklid geometrisi üzerine kurgulanmıştır. Şimdi, düz bir kağıt parçası yerine, bir silindir ya da bir küre gibi eğri yüzeye sahip bir kağıdınız olduğunu varsayalım.
Bu gibi yüzeyleri incelemek düz yüzeyleri incelemekten daha zordur, ancak yine de bu gibi yüzeylerde, bir üçgenin hipotenüsünün uzunluğunu, bir çemberin çevresini tahmin etmek için kullanılabilecek teoremler vardır. Bu tahminler, yüzeyin kavisli veya bükülmüş olduğu miktara bağlıdır. Riemann Geometrisindeki temel konulardan biri eğri yüzeylerin incelenmesidir.
1829’da Rus matematikçi Nicolai Lobachevsky, On the Principles of Geometry (Geometrinin İlkeleri) adlı kitabını yayınladı. Kendisi paralellik varsayımını yanlışlayan bir geometri hayal etti. Ondan birkaç yıl önce, Macar matematikçi Janos Bolyai’de benzer bir Öklid dışı geometri üzerinde çalışmıştı.
Bernhard Riemann’ın yaptığı da, Bolyai ve Lobachevsky’nin bulgularını genelleştirmek oldu. Günümüzde Lobaçevski geometrisi (hiperbolik geometri) ve Riemann geometrisi (eliptik geometri) olarak adlandırılan iki Öklid-dışı geometride Paralellik Aksiyomu şu şekilde yorumlanır.
- Düz bir yüzeyde bu noktadan geçen ve doğruya paralel olan yalnızca tek bir doğru vardır.
- Küresel bir yüzeyde bu noktadan geçen ve doğruya paralel olan hiçbir doğru yoktur.
- Hiperbolik yüzeyde bu noktadan geçen ve doğruya paralel olan sonsuz sayıda doğru vardır.
Bir Yüzeyin Eğriliği Ne Anlama Gelir?
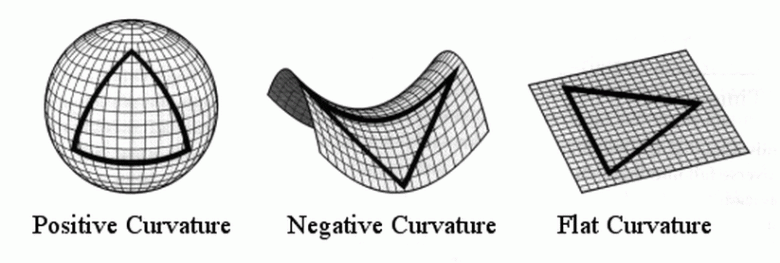
Eğriliği anlamanın en basit yolu, üçgenlerin davranışını dikkate almaktır. Sıfır eğrilikteki bir yüzeyde bir üçgenin iç açılan toplamı 180 derece, pozitif eğrilikteki bir yüzeyde açıları toplamı 180 dereceden büyük, negatif eğriliği olan bir yüzeyde ise açılar toplamı 180 dereceden küçüktür.
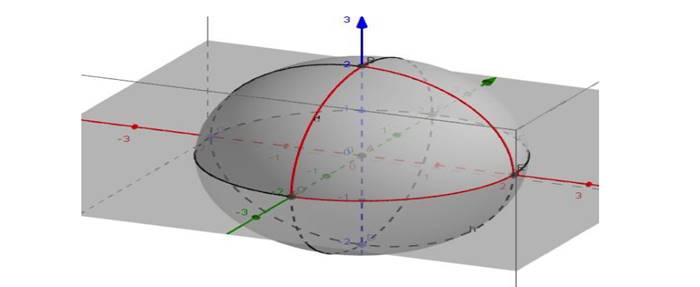
Bir kürenin yüzeyindeki iki nokta arasındaki en kısa mesafe düz bir çizgi değildir. Bunun yerine, kürenin yüzeyinde bulunan daire yaylarının parçasıdır. Şimdi küre üzerinde aynı doğru üzerinde olmayan yani aynı yayda bulunmayan üç nokta alalım.
Daha sonra bu noktaları birleştirelim. Şimdi aşağıda kırmızı çember parçalarıyla oluşturulmuş üçgene bakalım. Üçgenin köşelerinde kırmızı çember parçaları 90 derecelik açılarla kesişir. Dolayısıyla küresel geometride iç açıları toplamı 270 derece olan bir üçgen çizebiliriz.
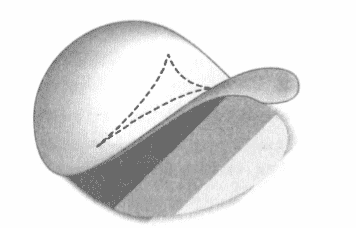
Peki, bir yüzey negatif eğrilikte nasıl olur? Bir başka değişle açılarının toplamı 180 dereceden küçük olan üçgenler nerededir? Bir paket Pringles açın cevabı göreceksiniz. Patates cipsinin eğri kısmı üzerine bir üçgen çizin. Üçgenin açılarının toplamı açık bir biçimde 180 dereceden az olacaktır. Negatif eğrilikteki yüzeylere hiperbolik yüzeyler denir. Hiperbolik yüzeyler üzerindeki paraleller gittikçe birbirlerinden uzaklaşırlar. Çünkü hiperbolik yüzey de sürekli olarak eğrilerek kendisinden uzaklaşmaktadır.
Küresel ve hiperbolik yüzeyler matematiksel olarak birbirlerinin tersidir. Örnek vermemiz gerekirse, küresel bir yüzeyden bir parça kesin ve kestiğiniz şeyi düzleştirmek için uğraşın. Yeterli malzememiz olmadığından başarılı olma şansımız yoktur.
Şimdi elimizde lastik bir Pringles olduğunu düşünün. Düzleştirmek istediğimiz zaman fazladan malzeme vardır. Bu nedenle de bir kısmı kendi üzerine katlanacaktır. Yani küresel yüzey kendi içine kapanırken hiperbolik yüzey genişler.
Hangi Geometri Doğrudur?
Üç geometride bulundukları yüzey bağlamında doğrudur. Öklid geometrisi, bir kağıt parçasına veya düz bir yüzeye çizilen şekiller için geçerlidir. Riemann geometrisi, bir kürenin yüzeyine çizilen şekiller için geçerlidir. Lobaçevski geometrisi ise sözde küre adı verilen bir hiperbolik yüzeylerde kullanılır.
Öklid dışı geometrilere uzun süre işe yaramaz gözüyle bakılsa da Einstein, içinde yaşadığımız üç boyutlu uzayın Öklid geometrisine değil, Öklid dışı geometriye uyduğunu gösterince düşünceler değişmiştir. Öklid dışı geometriler, insanın geometriyi doğru bir biçimde anlama, fiziksel uzayın gerçek niteliğini keşfetme girişimleri açısından hayati önemdedir. Göz atmak isterseniz: Düz, Küresel Ya da Hiperbolik: Evrenin Şekli Nasıldır?
Günümüzde Riemann Geometrisi diferansiyel geometrinin bir genellemesidir. Diferansiyel geometri, matematik ve Lineer Cebir kullanarak eğrilerin ve yüzeylerin geometrisini inceler. Riemann Geometrisi de bir Riemann metriği kullanarak düzgün manifoldların incelenmesini sağlar. ( Manifold matematikte topolojik bir uzaydır).
Kaynaklar ve İleri Okumalar:
- Explain branches of geometry for non-mathematician; https://math.stackexchange.com/
- A.L. Audichya; Mathematics: Marvels and Milestones; ISBN: 8189473409
- Non-Euclidean geometry; https://mathshistory.st-andrews.ac.uk
- How new geometries reshaped our world. yayınlanma tarihi: 9 Mayıs 2016; Bağlantı: https://plus.maths.org/
Matematiksel








