Günümüzde cebir dediğimiz zaman semboller ve aritmetik yardımı ile farklı türden denklemleri çözmek aklımıza gelecektir. Ancak birçok antik toplum, sembolik gösterim olmadan da iyi gelişmiş matematiksel sistemlere ve bilgiye sahipti. Örneğin geometriye yaptıkları katkılar ile hatırlanan eski Mısırlı matematikçiler, basit cebir problemlerini çözmede oldukça yetenekliydi. Bunun örneklerini günümüzde Rhind papirüsünde görmemiz olasıdır.

Antik Mısır’da erken döneme ait hiyeroglif rakamları tapınaklarda, taş anıtlarda karşımıza çıkar. Ancak bunların onların sayı sistemi ya da hesaplamaları hakkında çok az bilgi verirler. Ancak Mısırlılar kurumuş papirüs kamışının yapraklarını “kağıt” ve bir kamışın ucunu “kalem” olarak kullanmaya başlayınca daha hızlı yazma araçları geliştirdiler.
Birçoğu bir şekilde matematikle ilgili olan çok sayıda papirüs olduğu düşünülüyor ancak ne yazık ki malzeme oldukça kırılgan olduğundan neredeyse hepsi yok oldu. Geriye sadece iki önemli matematik belgesi hayatta kaldı.

Elimizdeki en eski matematik içerikli papirüsler MÖ 1800 ve MÖ 1650 tarihlerinde yazıldıkları düşünülen Moskova ve Rhind papirüsleridir. Üstü kesik bir piramidin hacminin ya da ölçüleri bilinen bir piramidin eğiminin hesaplanması gibi problemlerin çözüldüğü bu papirüsler, bize Mısır uygarlığının ulaştığı düzey hakkında da ipuçları veriyor.
Rhind Papirüsünün Keşfi Nasıl Oldu?
Ahmes Papirüsü olarak da bilinen Rhind Matematik Papirüsü, eski Mısır matematiği hakkındaki bilgimizin ana kaynağıdır. 1858 yılında İskoçyalı antikacı Alexander Henry Rhind tarafından Nil nehrinin Ramesseum yakınındaki Thebes’te bulunmuştur. Kâtip Ahmes (M.Ö. 1680 – 1620) tarafından yazılan papirüs, 6 metre uzunluğunda ve 35 cm genişliğindedir. 1868 yılından beri British Museum’da sergilenmektedir.

Papirüsün açılış paragrafında yazar, Kral III.Amenemhat döneminden bir metni kopyaladığını belirtir. Şimdi kaybolan orijinal metinin birkaç yüz yıl daha eski olduğu düşünülmektedir. Papirüsün merkezinden eksik olan bir parça yıllar sonra New York’ta bulundu ve 1922’den sonra Rhind Papirüsüne dahil edildi.
Eski Mısırlılar, muhasebe ve mühendislikteki görevleri yerine getirmek için aritmetiği kullanmakta çok ustaydılar. Bunu Rhind papirüsünde görebiliyoruz. Bu papirüs çarpma ve bölme işlemlerinin, denklem çözümlerinin, günlük pratik matematiksel hesaplamaların nasıl yapılacağına dair 85 problem içerir.

Papirüsün içerisinde kesirli sayılar, faiz hesabı, alan hesabı gibi konuların yanında saatin 60 dk., günün 24 saat ve dairenin 360 derece oluşu, pi sayısı ve Pisagor teoreminin temel bilgileri gibi pek çok önemli matematiksel bilgiler vardır.
Birim kesirler, doğrusal denklemler ve çözümleri, üçgen, dörtgen, yamuk, paralelkenarın alanları, trigonometriye ilk adım, dairenin alanı, benzer üçgenler de içeriğinde yer alan diğer konulardır. Rhind Papirüsü bir yerde uygulamalı matematik el kitabı gibidir.
Rhind Papirüsünde Bulunan Bazı Matematiksel Bilgiler
Mısırlılar özellikle çarpma ve bölme işlemlerini yapma biçimleri ilginçtir. Aslında bunu nasıl yaptıklarını Rus Çiftçi Ve Antik Mısır Çarpımı: Çarpma Yapmanın Eğlenceli İki Yolu başlıklı yazımızda kaleme almıştık. Ancak yine de bir örnek verelim. 19 ve 71 sayılarının çarpımını bulalım.
| 19’un İçinde Bulunan 2’nin Katları | 71 Sayısının Katları |
| 1 | 71 |
| 2 | 142 |
| 4 | 284 |
| 8 | 568 |
| 16 | 1136 |
16’dan sonra gelen çarpan 19’dan büyük olacağından 2’ye katlama işlemi burada durdurulur. Sol tarafta yer alan sayılardan hangilerinin toplamının 19 yaptığına bakmamız gerekir. Örneğimizde 16 + 1 + 2 = 19 olduğu için sağ taraftaki sütundan bunların karşılıklarını toplamalıyız. Sonucunda bu durumda 71 + 142 + 1136 = 1349 bizim çarpımımız olacaktır.

Eski Mısırlılarda bölme işlemi de benzer mantıktadır. Örneğin 91 sayısını 7’ye bölmek isteyelim. Aslında 7x = 91 eşitliğindeki x sayısını bulmak istiyoruz.
| 2’nin Katları | 7 Sayısının Katları |
| 1 | 7 * |
| 2 | 14 |
| 4 | 28 * |
| 8 | 56 * |
7 + 28 + 56 = 91 olduğundan bu sayılara karşılık gelen 1 + 4 + 8 = 13 sayısı bulunmak istenen x sayısını gösterecektir. Elbette bölme işlemi her zaman bu kadar kolay olmayabilir. Kesirli işlemler devreye girdiğinde işin rengi biraz değişir.
Mesela 35 sayısını 8’ e bölmek isteyen biri öncelikle 8’in 2 katını alarak işleme başlar ve işlemin adımları sonuç 35 sayısını geçtiğinde durur. Nihai olarak da işlemi yapan kişi, bölen sayısının yarısını alır. Aşağıdaki resimde işlemin adımları görülür. 8x = 35 eşitliğindeki x sayısının ne olduğunu elde etmek isteyen kişi 4 + ¼ + 1/8 = 4,375 sayısını bulacaktır.
| 19’un İçinde Bulunan 2’nin Katları | 8 Sayısının Katları |
| 1 | 8 |
| 2 | 16 |
| 4 | 32 * |
| 1/2 | 4 |
| 1/4 | 2 * |
| 1/8 | 1 * |
Antik Mısırlılar Kesirli İşlemleri Nasıl Yaptılar?
Eski Mısırlıların aritmetiği ile ilgili en dikkat çekici gerçek, kesirlerle ilgili yaptıkları çalışmalardır. Başa çıkmak zorunda oldukları tüm kesirleri birim kesirlerin toplamı biçiminde hesaplamışlardı. Ancak 6/7 kesrini; 6/7 = 1/7 + 1/7 + 1/7 + 1/7 + 1/7 + 1/7 olarak yazmamışlardır. Bunun yerine 6/7 = ½ + ¼ + 1/14 + 1/28 olarak göstermişlerdir. Ayrıca bu yazıya göz atmanızı öneririz. Mısır Matematiği Ve Pratik Uygulamalar İçin Horus’un Gözü
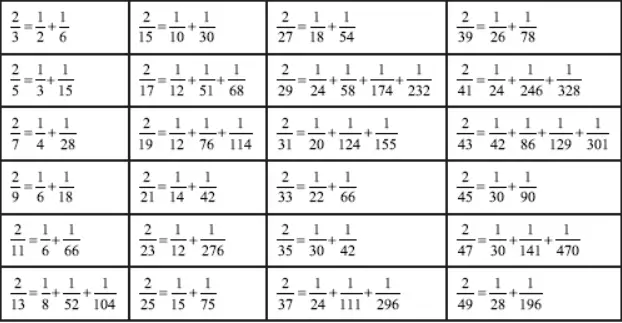
Rhind Papirüsü Hangi Tip Problemleri Barındırıyordu?
Rhind papirüsü başlangıcında kesir tabloları ardından da 84 tane problem içeriyordu. İlk kesir tablosu, el yazmasının büyük bir bölümünü kaplar.
- Papirüs, birkaç tane ‘tamamlama’ problemi içermektedir. Genellikle birkaç birim kesrin toplamıyla başlayan ve 1 sayısını elde etmek için bulunması gereken diğer birim kesirleri ne olduğunu soran problemleri barındırır. Mesela 22. problemde “2/3 + 1/30 toplamından 1 elde etmek için eklenmesi gereken birim kesirler ne olmalıdır?” sorusunun cevabı aranmıştır.
- 24. problemde “bir sayıya 1/7’si eklendiğinde 19 olan sayı kaçtır?” gibi bir bilinmeyenli denkleme ait basit sorular yer almıştır. Bu problemin modern gösterimi olarak “x + x/7” biçimindedir. Ancak Mısırlılar bu sorunun çözümünü deneme yanılma yöntemi ile bulmaya çalışmıştır.
- En eski “Aklından bir sayı tut” formatlı papirüsün 28. problemi ise şöyledir: Bir sayı düşünün. Bu sayıya kendisinin 2/3’ünü ekleyin. Sonucunda elde edilen toplamdan 1/3’ünü çıkarın ve cevabı bulun. Ayrıca papirüste bu problemin çözümü de ayrıntılı biçimde açıklanmıştır.
Bu papirüs tarım toplumu olan Mısırlıların kaygılarını içeren bir dua ile sonlanır. “Haşarat ve fareleri yakala, zararlı otları yok et; ısı, rüzgâr ve su bolluğu için Tanrı Ra’ya dua et!”
Kaynaklar ve ileri okumalar:
- O’Connor, J., and Robertson, E. 2000. An overview of Egyptian mathematics. School of Mathematics and Statistics at University of Saint Andrews, Scotland. [Online] Available at: http://mathshistory.st-andrews.ac.uk/HistTopics/Egyptian_mathematics.html
- Britannica, The Editors of Encyclopaedia. “Rhind papyrus”. Encyclopedia Britannica, 17 Jul. 2008, https://www.britannica.com/topic/Rhind-papyrus. Accessed 11 August 2024.
- Mathematics of the Pharaohs: The Rhind Papyrus and Ancient Egyptian Math. Yayınlanma tarihi: 14 Aralık 2019. Bağlantı: https://www.ancient-origins.net/artifacts-ancient-writings/rhind-papyrus-0013004
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel








