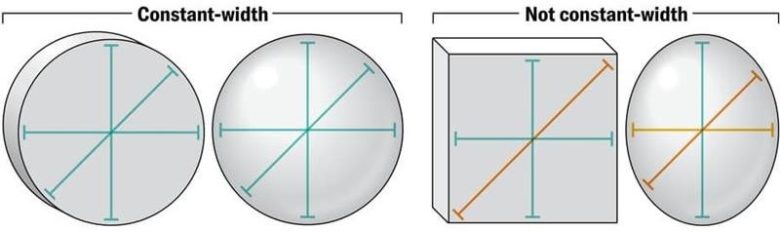
Çember sabit bir çapa sahiptir bu da cismin düzgün bir biçimde hareket etmesini sağlar. Ancak, sabit çapa sahip şekil sadece çember değildir. Aynı şeyi bir Reuleaux üçgeni ile de başarabilirsiniz.

Franz Reuleaux, Viktorya dönemi sanayi çağında ortaya çıkan yeni bir bilim insanı tipini temsil eder: mühendis ile bilim insanını bir araya getiren figür. Çalışmalarıyla büyük bir etki yaratmış ve “modern kinematiğin babası” olarak anılmıştır. Buna rağmen adı bugün daha çok, özel bir geometrik şekil ile hatırlanır.
Reuleaux, bu şekli 1875’te yayımladığı The Kinematics of Machinery adlı kitabında ele alır. Önce doğrusal hareketi sınırlayan mekanik düzenekleri inceler, ardından dönmenin hangi geometrik koşullarda mümkün ya da imkânsız hâle geldiğine geçer.

Bir eğriye dıştan teğet olan iki paralel doğru, bu eğrinin genişliğini belirler. Eğer eğrinin genişliği yönüne göre değişiyorsa, bu doğrular eğrinin serbestçe dönmesini engeller. Genişlik her yönde aynıysa, bu engel ortadan kalkar. Çemberin özel olmasının nedeni de budur.
Reuleaux burada önemli bir noktaya dikkat çeker: Sabit genişlik yalnızca çembere özgü değildir. Dairesel yaylar kullanılarak başka sabit genişlikli şekiller de kolayca oluşturmak mümkündür.
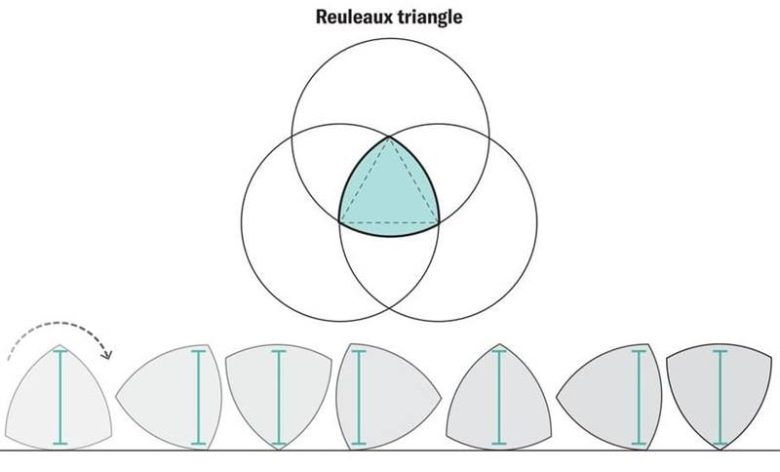
Ardından bunun en basit örneğini verir. Bir eşkenar üçgenin her köşesini merkez alıp, karşıdaki iki köşeden geçen yaylar çizildiğinde ortaya özel bir eğri çıkar. Bu eğri bugün Reuleaux üçgeni olarak bilinir. Reuleaux ise bu şekli “eşkenar eğri üçgen” olarak adlandırır.
Reuleaux Üçgeni Nasıl Çizilir?
Bu şekli siz de kolayca çizebilirsiniz. Bunun için önce bir kenarı x cm uzunluğunda bir eşkenar üçgen çizin. Ardından pergelinizi x cm açıklığa ayarlayın. Pergelin ucunu üçgenin köşelerinden birine yerleştirip, karşıdaki iki köşeden geçecek şekilde bir çember çizin. Aynı işlemi üç köşe için de tekrarlayın. Ortaya çıkan bölge, Reuleaux üçgeni olacaktır.
Reuleaux üçgeninin bir başka şaşırtıcı özelliği, bu biçimde tasarlanan bir matkap ucunun yuvarlak değil, kareye yakın bir delik açabilmesidir. Başka bir deyişle Reuleaux üçgeni, uygun boyutlardaki bir karenin içinde dönerken her an karenin iki kenarıyla temas hâlinde kalır ve bu hareket kare biçimli bir deliğin oluşmasını sağlar.
Alman mühendis Felix Wankel’in (1902–1988) tasarladığı Wankel motoru, Reuleaux üçgeni biçiminde dönen bir parçaya sahip bir içten yanmalı motordur. Bu tasarım, motorun daha az hareketli parça kullanmasını sağlar ve aynı boyuttaki klasik pistonlu motorlara kıyasla daha yüksek güç üretmesine olanak tanır.
Günlük Hayatımızda Reuleaux Üçgeni

Bu şekil, hem antik hem de modern mimaride sıkça karşımıza çıkar. Ustalar onu kimi zaman taş işçiliğinde ince bir ayrıntı olarak işler, kimi zaman pencere ya da kapı formuna dönüştürür.
Bazı Amerikan kentlerinde yetkililer, yangın musluklarının vanalarını yetkisiz erişime karşı korumak için bu biçimde somunlar tercih eder. Çünkü sıradan anahtarlar bu somunların etrafında kayıp gider. Gitar yapımcıları da penaları çoğunlukla bu biçimde tasarlar. Bu sayede pena elde rahatça durur ve tellere dengeli biçimde temas eder.
Bu eğri, zarif biçimiyle Leonardo da Vinci’nin de dikkatini çekmiştir. Da Vinci’nin notları arasında, Dünya’yı sekiz parçaya ayıran ve her bir parçayı Reuleaux üçgeni biçiminde düzleştiren bir dünya haritası taslağı yer alır.

Reuleaux üçgeninin sıra dışı özellikleri, gündelik yaşamda sandığımızdan çok daha fazla yerde karşımıza çıkar. Üç eş eğimli kenarı ve sabit genişliği, bu şekli pek çok uygulama için cazip hâle getirir. Yapısal kararlılığı ve görece küçük çevresi de mimari ve mekanik tasarımlarda onu sıkça tercih edilen bir form yapar.
Bu yazıdan sonra etrafınıza biraz daha dikkatli bakarsanız, büyük olasılıkla siz de bu üçgenlerden birkaçına rastlayacaksınız.
Kaynaklar ve ileri okumalar:
- Arman, Andrii & Bondarenko, Andriy & Nazarov, Fedor & Prymak, Andriy & Radchenko, Danylo. (2024). Small volume bodies of constant width.
- Shape with constant width irrespective of dimensions amazes mathematicians. Yayınlanma tarihi: 21 Haziran 2024. Kaynak site: Bağlantı: Shape with constant width irrespective of dimensions amazes mathematicians
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel





