Matematikçiler ona yeni bir şekil vererek “tekerleği yeniden icat ediyorlar”. Bu çığır açan buluş, hayal edemeyeceğimiz boyutlarda nesnelerin nasıl inşa edileceğini göstererek onlarca yıllık bir geometri problemini de çözüyor.

Bir tekerleğin yuvarlanma nedeni, sabit genişliğe sahip bir nesne olmasındandır. Bu geometrik özellik, tekerleklerin hareket ederken zemin ve araba gibi iki paralel düzlem arasında sabit bir mesafeyi korumasını sağlar.
Esasen, bir şekil yalpalamadan düzgün bir şekilde yuvarlanabiliyorsa sabit genişliğe sahiptir. Örneğin, paralel duran ellerinizin arasına bir tenis topu koyun ve döndürün. Topun sabit genişlikte bir geometrisi olduğu için ellerinizin asla birbirine yaklaşmadığını veya uzaklaşmadığını göreceksiniz.
Yumurta veya dikdörtgen kutu gibi geometrik forma sahip bir şekil ise bu testi asla geçemez. Aşağıdaki görselde sabit bir genişliğe sahip olan ( solda) ya da olmayan ( sağda) geometrik şekilleri görebilirsiniz.
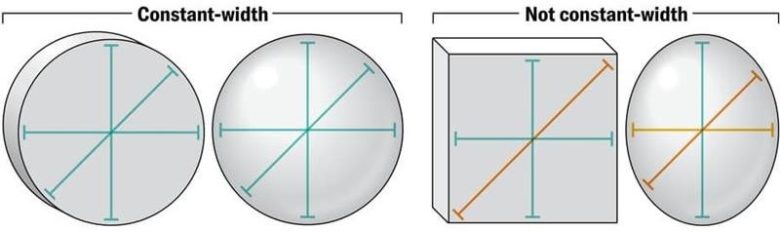
Daireler ve küreler sabit genişlikteki şekillerin basit örnekleridir. Bu nedenle de bu şekiller yıllardır hareketi kolaylaştırmak için kullanılmaktadır. Bu tip geometrik şekillerin tüm sınır noktaları merkezden eşit uzaklıktadır.
Daire iki boyutludur ve küre ise üç boyutludur. Ancak daha yüksek boyutta ve aynı tanıma sahip nesneler de vardır. Sorun şu ki bu nesneleri hayal gücümüzde canlandırmamız ya da buraya bir örneğini eklememiz kolay değildir. Ancak yine de bu matematikçiler için bir engel olmayacaktır.
Bu şekillerin hepsinin de ortak bir özelliği vardır. Sınır noktalarının hepsi merkezi bir noktadan sabit bir uzaklıkta olduğundan, bu şekillerin hepsi maksimum alan ya da hacme sahiptirler. Ancak bu kadar hacimli olmak her zaman ideal değildir. Bu nedenle 1980’lerde matematikçi Oded Schramm şu soruyu ortaya attı. Herhangi bir boyutta minimum hacme sahip sabit genişlikte şekilleri nasıl bulabiliriz?
Bu soruya bir cevap 2024 yılı Haziran ayına kimse cevap veremedi. Ancak ön baskı sunucusu arXiv.org’da yayınlanan bir çalışma herhangi bir boyuttaki sabit genişlikteki şekillerin araştırılmasına öncülük ediyor. Çalışmanın detaylarını kavramak için konuyu iki veya üç boyutta aktarmamız gerekiyor.
Reuleaux üçgeni ve genellemesi

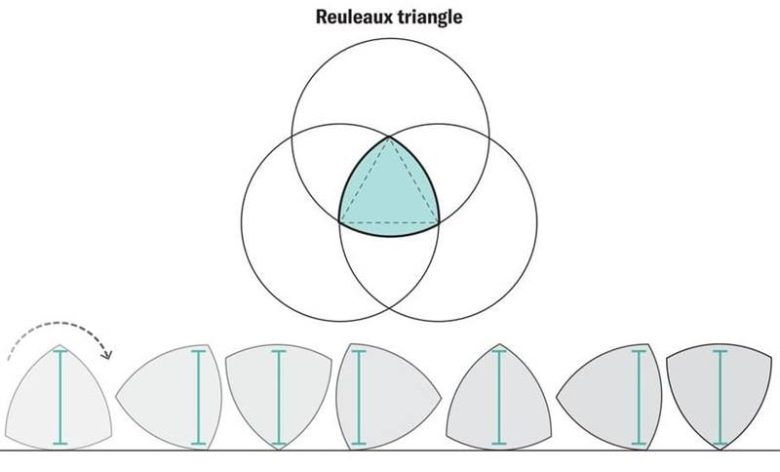
İki boyutta, Reuleaux üçgeni sabit genişlikteki şekillerin en küçük alanına sahiptir. Reuleaux üçgeni, bir eşkenar üçgenin her bir köşesinde eşit yarıçaplara ve merkezlere sahip üç dairesel yaydan oluşur. Bu şekli kolayca kendiniz de çizebilirsiniz.
Şimdi bir pergel alan ve genişliğini x cm olarak ayarlayın. Pergelin ucunu köşelerden birine koyun ve karşısında kalan iki köşeden geçecek biçimde bir çember çizin. Bu işlemi üç defa tekrarlayın. Aşağıdaki görselde mavi boyalı kısım bir Reuleaux üçgenidir. Bu şeklin de aynı çember gibi sabit bir genişliği vardır. Sonucunda bu da onu birçok amaç kullanılan yararlı bir geometrik şekil yapar.
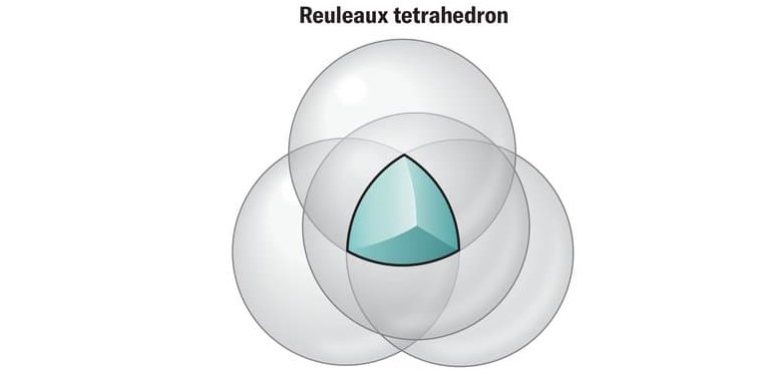
Üç boyutta da, benzer bir yöntem kullanabilirsiniz. Dört eşkenar üçgenden oluşan bir şekil olan düzenli bir tetrahedron alın. Sonra her bir köşesine bir küre ekleyin. Bu üst üste binen kürelerin merkezinde ortaya çıkan şekile Reuleaux tetrahedron denir. Tam olarak sabit genişlikte değildir ancak ona yakındır. Biraz zımparalama, sabit genişlikte bir şekil oluşturur.
Ancak bu şekillerin ardındaki basit formüller, dört veya daha fazla boyutta nasıl inşa edileceğine dair hiçbir içgörü sunmuyordu. En son çalışma, yöntemi genişleterek herhangi bir boyutta sabit genişlikte nesneler oluşturmak için genel bir algoritma sağlıyor.
Matematikçiler istenen yeni şekli elde etmek için ilgili iki boyuta benzer bir yaklaşım kullandı. Bunun nasıl yapıldığını aşağıdaki animasyondan izleyebilirsiniz. Sonuçta ortaya çıkan şekil, Reuleaux üçgeninin bir genellemesi olan Reuleaux tekerleğidir.
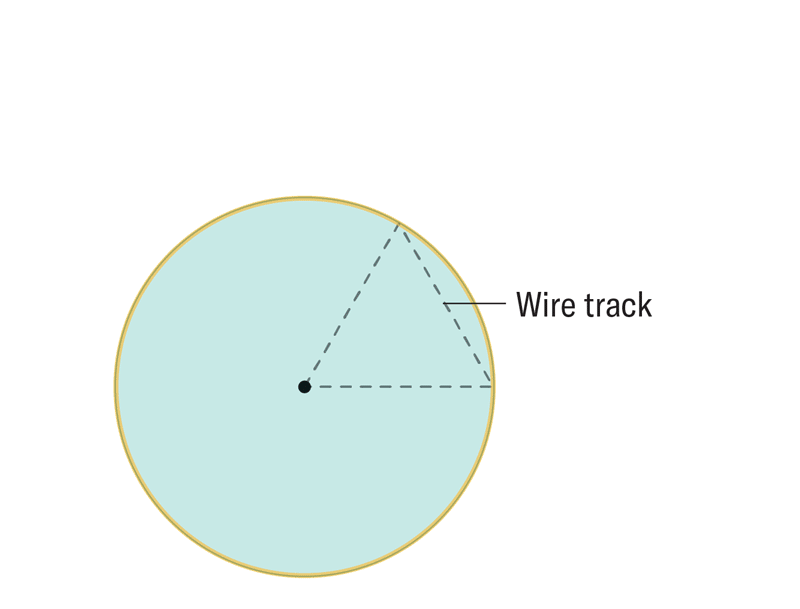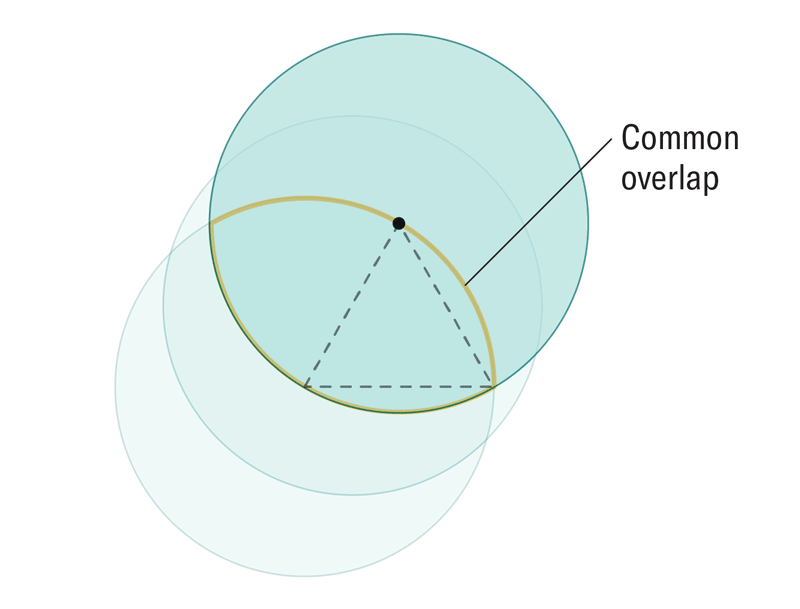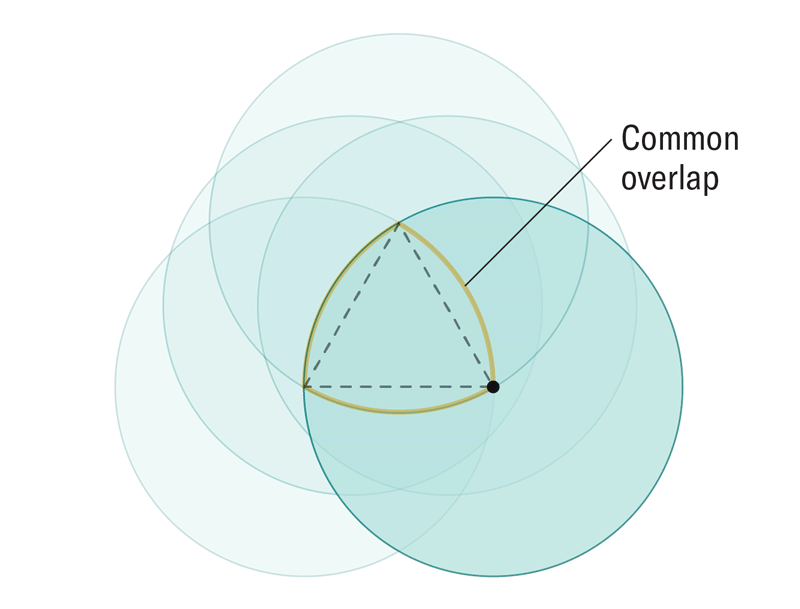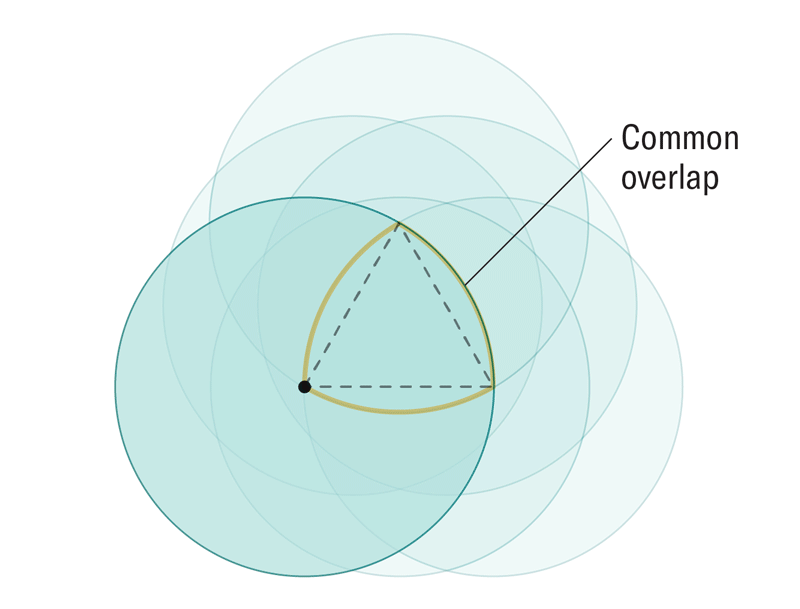
Reuleaux tekerleği problemin çözümü olabilir
Bu teknik, herhangi bir boyutta sabit genişlikte bir nesneyi ortaya çıkarabilir. Bu yaklaşım, yalnızca sabit genişliği garantilemekle kalmaz. Aynı zamanda hacimlerini daha yüksek boyutlu uzayda hesaplamayı da kolaylaştırıyor. Son çalışma şeklin boyutundan bağımsız olarak yalnızca iki değişkeni içeriyor. Bu da kanıtın oldukça basit olmasını sağlıyor.

Yeni nesnenin hacmi, n boyutlu bir toptan 0,9 n kat daha küçüktür. Bu da hacmin her ek boyutla birlikte üstel olarak azaldığı anlamına gelir. Diğer bir deyişle daha yüksek boyutlarda şekil eşdeğer boyuttaki küreden orantılı olarak daha küçük olacaktır ve tüm bu şekiller tam bir yuvarlak olmasa da yine de yuvarlanacaktır. Bu da matematikçi olan Oded Schramm tarafından ortaya atılan problemin çözümü anlamına gelebilir.
Kaynaklar ve ileri okumalar
- Shape with constant width irrespective of dimensions amazes mathematicians. Yayınlanma tarihi: 21 Haziran 2024. Kaynak site: Bağlantı: Shape with constant width irrespective of dimensions amazes mathematicians
- Arman, Andrii & Bondarenko, Andriy & Nazarov, Fedor & Prymak, Andriy & Radchenko, Danylo. (2024). Small volume bodies of constant width.
- Mathematicians Reinvent the Wheel in Higher. Dimensions to Solve Decades-Old Geometry Problem. yayınlanma tarihi: 7 Ağustos 2024. Kaynak site: Scientific American. Bağlantı: Mathematicians Reinvent the Wheel in Higher. Dimensions to Solve Decades-Old Geometry Problem
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel





