Rasgele seçilmiş n tane kişiden oluşan bir gruptan en az iki kişinin aynı doğum gününe sahip olma olasılığı nedir? Bu soru bir olasılık problemi gibi görünse de cevabı duyduğunuzda buna “doğum günü problemi” değil de “doğum günü paradoksu” denmesinin nedenini anlayacaksınız.

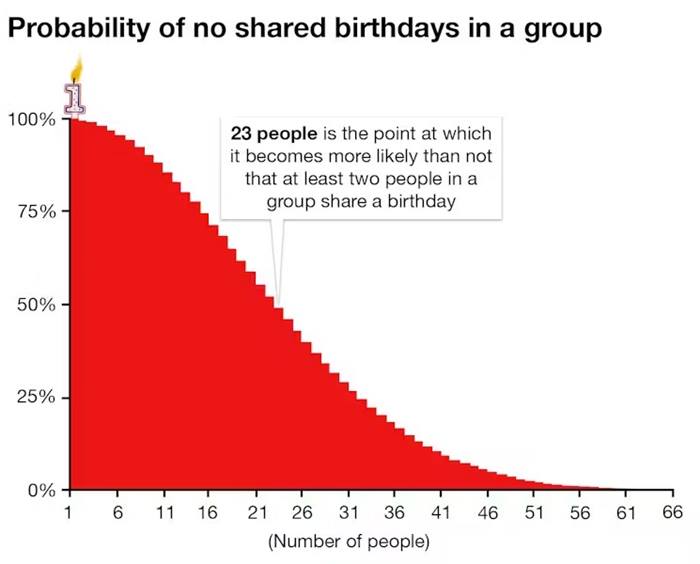
Doğum Günü paradoksu çoklu karşılaştırma yanılgısının klasik bir örneğidir. Aslına bakarsanız, 23 kişilik bir grupta (doğum günlerinin her birinin yılın bağımsız olarak seçilmiş bir günü olduğunu ve tüm günlerin eşit olasılıkla gerçekleştiğini varsayarsak), gruptan en az ikisinin aynı doğum gününe sahip olması ihtimali hiç olmamasından daha yüksektir.
Eğer 23 kişilik bir grup ele alırsak, bu grupta iki kişinin aynı doğum gününe sahip olma olasılığı %50’dir. 35 kişilik bir grupta, bu oran yaklaşık % 80’dir. Odada 57 kişi var ise ikisinin doğum gününün aynı olma olasılığı yaklaşık %99’dur.

İnsanlar genellikle kendi doğum günlerini paylaşan biriyle tanışmalarının nadir olduğunu düşünerek buna inanmazlar. Ama şaşırtan şey matematik değil, sezgilerimizdir. Matematik yalan söylemez. Sezgilerimizle matematik arasında kalırsak, matematiğe güvenmeliyiz. Yalnızca iki kişiyi seçerseniz, aynı doğum gününü paylaşma şansları elbette düşüktür. (yaklaşık 365’te 1, yani %0,3’ten az). Ancak kişi sayısı arttıkça sonuç da ilginçleşmeye başlayacaktır.
Şimdi bunun nasıl olduğunu anlamaya çalışalım. Hiç artık yıl olmadığını, sınıfta hiç ikiz olmadığını ve doğum günlerinin düzgün dağıldığını varsayalım. Ayrıca grubun içindeki insanların 365 günün herhangi birinde doğma olasılıklarının eşit olduğunu kabul edelim. Yani her birinin belli bir günde doğma olasılığı 1/365 olsun.
Doğum Günü Problemi Çözümü
Doğum günlerinin aynı olması için bize bir çift insan lazım. Ardından olası çift sayısını göz önüne almalıyız. Örneğin odada 3 kişi var ise ( A,B,C) incelememiz gereken A – B, A – C ve B – C çiftleri olacaktır. Dört kişi için incelememiz gereken altı çift vardır. Matematikte bunu hesaplamak için kombinasyon formülü kullanırız. Bu durumda 23 kişi ile C(23 , 2)=23 x 22/2 hesabını yaparsak 253 farklı çift elde ederiz. Yani 23 kişiyle ortak doğum gününe sahip olabilecek 253 çift insan vardır.
Şimdi, 23 kişilik bir grupta, A olayını “iki kişinin doğum gününün aynı olması” olarak tanımlayalım. A olayının gerçekleşme olasılığını, yani P(A) ile gösterdiğimiz değeri bulmak istiyoruz. Bunu bulmak yerine A olayının gerçekleşmeme olasılığını (bunu da P(A’) ile gösterelim) bulmaya çalışalım. Burada A’ olayı; “iki kişinin doğum gününün aynı olmaması” anlamına geliyor. Bir olayın gerçekleşme olasılığı en fazla 1 olur. Bu durumda bir olayın gerçekleşmeme olasılığını bulmak için de birden çıkarmamız gerekecektir.
Şimdi 23 kişiyi tek tek numaralandırdığımızı düşünelim. Birinci kişinin belli bir günde doğmuş olma olasılığı bir yani 365/365’dir. İkinci kişinin doğum günü birinci kişi ile aynı olamaz. Bu nedenle ikinci kişinin ilk kişiden doğum gününün farklı olma ihtimali 364/365 olacaktır. Üçüncü bir kişinin doğum gününün bu ikisinden farklı olma ihtimali 363/365 olur.

Bu mantığı 4, 5, 6, … kişi için sürdürürsek doğum günü probleminin gizemini çözebiliriz. 23’üncü kişiye geldiğimizde kimsenin doğum gününün aynı olmama ihtimali için hesap makinemizde 0,4927 sayısını görürüz. Bunun tersi, yani “en az iki kişinin doğum günün aynı olma ihtimali ise 1- 0,4927=0,5073 kadar olacaktır. Sonuçta bu sayı yüzde 50 den büyüktür.
Sonuç olarak
Evet, herhangi ortak bir doğum günü bulunmasının % 50 kesinlik kazanması için en az 23 kişinin bulunması gerekir. Ancak bu belirli doğum günleri, örneğin 19 Mart, için geçerli değildir. 19 Mart gibi belirli bir doğum gününün gruptan birinin doğum günü olmasından % 50 emin olabilmek için daha büyük bir grup, tam bir sayı vermek gerekirse 254 kişi gerekecektir.
Gördüğünüz gibi kişi sayısı 365’e yaklaştıkça A olayının gerçekleşmesi %100’e yakınlaşır. Peki ne zaman bu olasılık tam olarak %100 olur? Elbette grupta 366 kişi olursa. Eğer 365 kişi yılın farklı günlerinde doğmuşsa, mecburen 366’ncı kişinin doğum günü, gruptaki başka birinin doğum günüyle aynı olmak zorundadır. Buna matematikte güvercin yuvası ilkesi diyoruz.
Kaynaklar ve ileri okumalar:
- Paradoxes of probability and other statistical strangeness. Yayınlanma tarihi: 4 Nisan 2017. Kaynak site: Conversation. Bağlantı: Paradoxes of probability and other statistical strangeness
- Check your intuition: The birthday problem – David Knuffke; yayınlanma tarihi:4 Mayıs 2017; Bağlantı: https://ed.ted.com/
- What is the birthday paradox?; yayınlanma tarihi: 30 Temmuz 2022; Kaynak site: L,ive Sceince. Bağlantı: What is the birthday paradox?
- Ahmet Çevik – 50 Soruda Paradokslar – Bilim ve Gelecek Kitaplığı
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel