Doğadaki bir çok şey karmaşık bir biçimde hareket eder. Bu karmaşık hareketleri rastgele yürüyüş sayesinde anlayabiliriz.
Açık havaya çıktığınız zaman yüzünüzde hissettiğiniz sıcaklık, size güneşten gelen sayısız foton tarafından ulaştırılır. Ama inanın ya da inanmayın, bu fotonlar tıpkı bir bardan eve dönen sarhoş bir insan gibi veya bir torba kahveyi açtığınızda aldığınız ilk koku gibi hareket eder.
Fizikte bilinen en hızlı hızda seyahat eden bu fotonlar, güneşten Dünya’ya yaklaşık sekiz dakikada ulaştı. Buna karşılık, yolculuğun ilk %0,05’i yani güneşin çekirdeğinden yüzeyine kadar gitmesi yaklaşık 170.000 yıl sürdü. Çünkü boş uzayın aksine, Güneş’in içi kalabalık bir yerdir.

Hatta o kadar kalabalıktır ki, ışık hızındaki bir foton, Güneş’in atomlarından birine çarpmadan önce sadece yaklaşık bir milimetrelik bir alanı geçecektir. Foton yüzeye ulaşma sürecindeyken, her seferinde rastgele bir yöne doğru savrulacaktır. Amaçsız bir yolda sürüklenir ve sonunda güneşten kurtulmayı başarır.
Bu olağanüstü yolculuk hakkındaki bilgimiz, bu tür rastgele fiziksel süreçlerden öngörülebilir davranışlar çıkarmamızı sağlayan rastgele yürüyüşlerin modern matematiksel teorisine çok şey borçludur.
Hareketi anlamaya ve tanımlamaya çalıştığınızda kendinizi hemen matematiğin dilini kullanırken bulursunuz. Ancak matematiksel hareket tanımlamaları bazen farklılaşır. Buna bir örnek matematikçilerin rastgele yürüyüş veya sarhoş yürüyüşü dediği şeydir.
Rastgele yürüyüş (Random walk) nedir?
Rastgele yürüyüşün ne olduğunu anlamak için bir bahçenin ortasında bir yerde durduğunuzu düşünün. Şimdi rastgele bir yön seçin ve o yönde bir adım yürüyün. Sonra rastgele başka bir yön seçin ve o yönde bir adım daha yürüyün. Ve böyle yürümeye devam edin. Bu yürüyüşünüzü GPS’e kaydetme şansınız olursa belli bir süre ve adım sonucunda yürüdüğünüz yol haritada aşağıdakine benzer olacaktır.
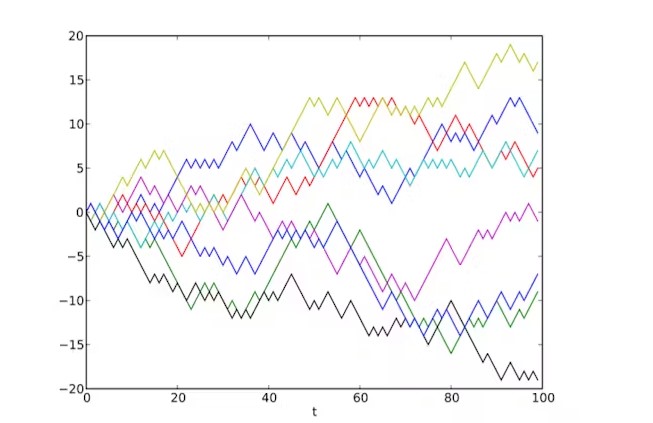
Rastgele hareketin en basit türü, yalnızca belirli bir yönde ve aynı büyüklükteki adımlarla hareket edilmesine izin verilen ayrık tek boyutlu rastgele yürüyüştür. 100 adım boyunca bu tür sekiz yürüyüşün ilerlemesini takip edersek, yukarıdaki gibi grafiklere sahip olabiliriz.
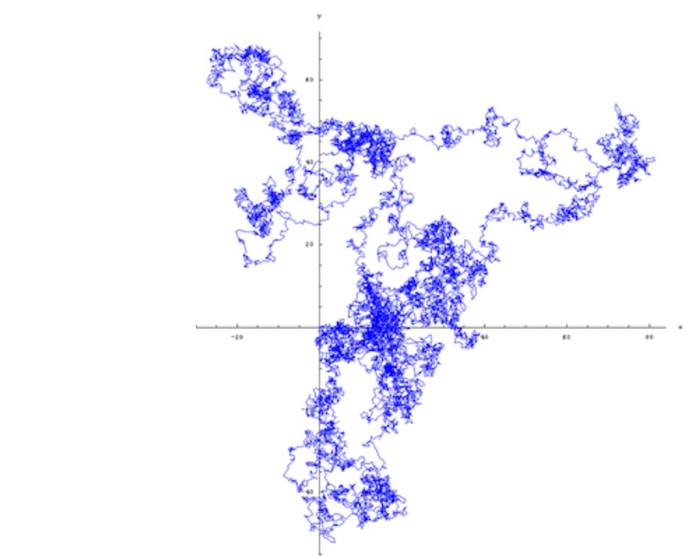
İki boyutlu rastgele yürüyüşler, genellikle sarhoş bir bar müşterisinin evine dönüş yolculuğu ile gösterilmektedir. Sonuçta kafası güzel olduğu için iki adım öne atıp sonra aniden sağa doğru sendeler. Ardından sola adım atıp iki boyutlu rastgele bir yürüyüşle yoluna devam edecektir. ( Ancak adımları hala aynı uzunluktadır). Onun hareketinin bir örneği aşağıdaki gibi olacaktır.
Rastgele yürüyüşler neden önemlidir?
Bu tür rastgele yürüyüşler yiyecek arayan hayvanların gezintilerinden kimyasal polimerlerin kıvrımlarına kadar neredeyse tüm rastgele aktivitelerin modellenmesinin temelini oluşturur. Aslında daha başka rastgele yürüyüş örnekleri de vardır. Örneğin her aşamada yalnızca yönü rastgele seçmediğinizi, aynı zamanda o yöne doğru kat ettiğiniz mesafeyi de (yani tek bir adım olmadığını) hayal edin.
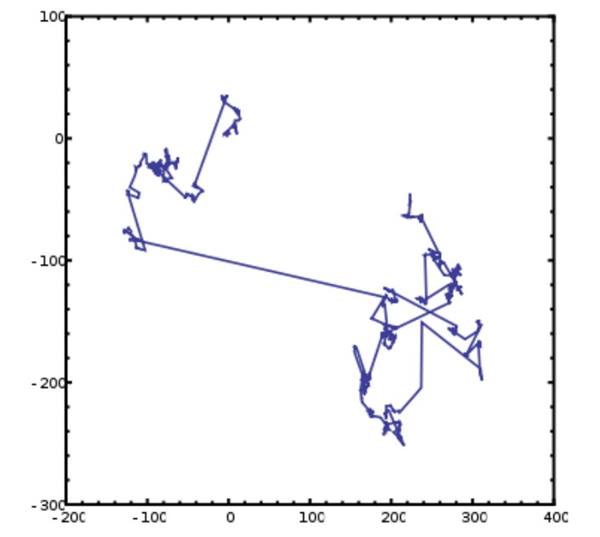
Bu tür rastgele yürüyüşlere Lévy yürüyüşleri denir ve köpeğinizi bir parkta tasmasız bıraktığınızda gördüğünüz şeye benzer. Küçük bir alanı koklayacak, sonra başka bir alanı koklamak için rastgele bir yöne doğru fırlayacak ve bu böyle devam edecektir.
1900’deki doktora tezinde rastgele yürüyüşlerin tutarlı bir matematiksel teorisinin temellerini atan Fransız matematikçi Louis Bachelier, bu rastgele yürüyüşlerin çarpıcı bir özelliğini ilk fark eden ilk kişiydi. Buna göre rastgele yürüyüşçünün gelecekteki davranışını tahmin etmek istiyorsanız, yalnızca şu anda nerede olduklarını bilmeniz yeterlidir. Sonrasını matematik yapacaktır.
Örneğin, yeterince uzun bir zaman verildiğinde, yürüyüşçünün sonunda başlangıç noktasına geri dönme olasılığını hesaplayabiliriz. Mesela, iki boyutlu bir yüzeyde yürüyen sarhoş bir arkadaşın yeterince uzun süre yürümesine izin verirseniz, başlangıç noktasına geri dönmesi neredeyse kesindir. Öte yandan, üç boyutlu rastgele yürüyüşler için, başlangıç noktasına geri dönme şansı üçte birdir. Bu nedenle fotonlar sonunda güneşten uzaklaşırlar.
Sürekli rastgele yürüyüşler nedir?
Romalı filozof Lucretius’un MÖ 60 civarında gözlemlediği gibi, güneş ışınları beklenmedik bir doğa olayına da ışık tutacaktır. 20. yüzyılın başında fizikteki en büyük beyinler Brown hareketi olarak adlandırılan bir olguya dikkatlerini vermişlerdi. Kökenlerinin açıklanması ise, atomların varlığına dair ilk kesin kanıtı sağlayacaktı.

Bitkibilimci Robert Brown mikroskobuyla sudaki polen taneciklerine baktığında, minik parçacıkların polenden koptuğunu görmüştü. Fakat su hiç kıpırdamazken bile bu parçacıklar yerlerinde durmuyor, sürekli kıpraşıyorlardı. Brown önce parçacıkların canlı olduğunu varsaydı, fakat sonradan aynı şeyi canlı olmayan maddelerde de gözlemledi.
Ne yazık ki kendisi asi polen taneciklerinin sırrını hiçbir zaman çözemedi. Ancak bu garip olay hakkında bir yazı yayımladı. Sonraki yıllarda başkaları da aynı olayı gözlemledi. Farklı kişiler farklı açıklamalar getirdiyse de gizem hakkıyla çözülemedi. Bu konudaki asıl ilerleme için, 26 yaşındaki Albert Einstein’ı beklemek zorundaydık.
Einstein, Brown hareketinin neden meydana geldiğine dair ayrıntılı bir açıklama yaptı. Parçacıklar o kadar küçüktü ki, çevredeki atomlar ve moleküllerle çarpışmalarla ileri geri savruluyorlardı. Einstein, Brown hareketini rastgele bir yürüyüş olarak modelledi. Adımları atanlar ise çarpışmalar ile yönlendirilen moleküllerdi.

Onun bu düşünce biçimi tek tek moleküllerin boyutlarına ilişkin ilk tahminlerin yapılmasını mümkün kıldı. Einstein’ın denklemleri dört yıl sonra Fransız fizikçi Jean Perrin tarafından deneysel olarak doğrulandı. Bu da uzun zamandır şüphelenilen atomların varlığına dair ilk kesin kanıtı sağladı.
Belirli bir sayı üzerinde yürümek
Rastgele yürüyüşlerin matematiği, sayılar ile ilgili yapılan analizlerde de son derece faydalıdır. Belirli bir sayı üzerinde iki boyutlu bir yürüyüş yapmak için, iki boyutlu sarhoş yürüyüşüne benzer bir süreç kullanırız. Ancak bu sefer, adım yönlerini rastgele seçmek yerine, sayının kaçlık tabanda yazıldığına bakarız (örneğin ikili veya ondalık) ve bu tabandaki rakamları, bir sonraki adımda nereye gideceğimize dair bir dizi talimat olarak kullanırız.
1/3 (ondalık açılımı 0.333333… olan) gibi bir sayı bu açıdan ilgi çekici değildir. Sonucunda yürüyüş sonsuza dek aynı yönde devam edecektir. Ancak rakamları 3.141592… ile başlayan ünlü pi (π) sayısı üzerinde bir yürüyüş çok daha büyüleyicidir. Örneğin bu sayede π’nin ilk 100 milyar rakamı için aşağıdakine benzer bir sonuç elde edebilirsiniz.

Gördüğünüz gibi, π üzerindeki bu uzun yürüyüş, rastgele bir yürüyüş ile çarpıcı bir biçimde birbirine benziyor. Aslında bu bir tesadüf değildir. Rastgele hareketin mevcut olduğu her an, rastgele yürüyüş teorisinin matematiği, öngörülemez olan şeylerden öngörülebilir özellikler çıkarmamızı sağlayacaktır.
Kaynaklar ve ileri okumalar
- Tipsy tottering, sunlight and the smell of coffee: it’s all random. Yayınlanma tarihi: 18 Aralık 2013. Kaynak site: Conversation. Bağlantı: Tipsy tottering, sunlight and the smell of coffee: it’s all random
- To know how it works, see how it moves. Yayınlanma tarihi: 13 Şubat 2024. Kaynak site: Plus math. Bağlantı: To know how it works, see how it moves
- Aragón Artacho, Francisco Javier & Bailey, David & Borwein, Jonathan (Jon) & Borwein, Peter. (2013). Walking on Real Numbers. The Mathematical Intelligencer. 35. 10.1007/s00283-012-9340-x.
- Viswanathan GM, Buldyrev SV, Havlin S, da Luz MG, Raposo EP, Stanley HE. Optimizing the success of random searches. Nature. 1999 Oct 28;401(6756):911-4. doi: 10.1038/44831. PMID: 10553906.
Matematiksel






