Rastgelelik önemlidir. Bir anket yaptığınızda, sonucun güvenilir olabilmesi için katılımcıların rastgele seçilmesi gerekir. Bir piyango bileti aldığınızda ise, bilet numaranızla eşleşmesini umduğunuz sayıların gerçekten rastgele seçilmiş olmasını istersiniz. Peki, rastgele sayılar tam olarak nedir? Ve neden bazı şeyler rastgele görünse de aslında tamamen rastgele olmaları her zaman mümkün değildir?

Gerçek dünyada olasılığı tanımlamak zordur. Zar attığımızda beş gelme olasılığının altıda bir olduğunu söyleriz, çünkü hangi yüzün üste geleceğini öngörecek kadar bilgiye sahip değiliz. Oysa bu olay tamamen rastgele değildir. Elimizin hareketiyle zara etki eden tüm kuvvetleri bilseydik, sonucun ne olacağını hesaplayabilirdik.
Pratikte bu kadar veriye ulaşmak mümkün olmadığından, olasılığı “rastgele” olarak kabul ederiz. Matematikçiler bu durumu “sözde rastgelelik” olarak tanımlar; çünkü olay bize rastgele görünse de, yeterli bilgiye sahip olsaydık aslında öyle olmadığını bilirdik.

Benzer şekilde, Google’dan rastgele bir sayı üretmesini istediğimizde, bu sonucu verebilmesi için belirli bir sürece ihtiyaç duyar. Ancak Google’ın tamamen teorik, matematiksel anlamda rastgele modeller kullanma imkânı yoktur.
Bunun yerine, rastgelemiş gibi görünen ama aslında belirli bir sürece dayanan sayılar üretir. Biz bu süreci ya da girdilerden bazılarını bilmediğimiz için sayı bize rastgele görünür. Dolayısıyla Google’ın ürettiği bu sayı da “sözde rastgele”dir.
Diyelim ki elimizde bir sayı kümesi ya da daha genel bir ifadeyle uzaydaki bir nokta topluluğu var. Bu noktaların gerçekten rastgele bir süreçten mi, yoksa belirli bir kurala dayalı bir süreçten mi üretildiğini nasıl anlayabiliriz?
Bu soru, matematiğin birçok alanında temel bir konudur. Matematikçiler, rastgeleliği tespit etmek için çeşitli testler geliştirir. Ancak şu sorular da önemlidir: “Bu testler ne kadar güvenilir? Rastgele üretilmemiş ama testleri geçebilen kümeler var mı?” Eğer varsa, bu tür kümelere “sözde rastgele” denir.
Rastgeleliği nasıl tespit edebiliriz?
Bunun en basit yollarından biri, “Tekdüze dağılım” adı verilen bir kavramdır. İki kare kutu düşünelim; her ikisinde de rastgele serpiştirilmiş gibi görünen noktalar olsun. Ancak kutulardan birinde noktalar tüm alanı doldururken, diğerinde kare alanın yarısı boştur.
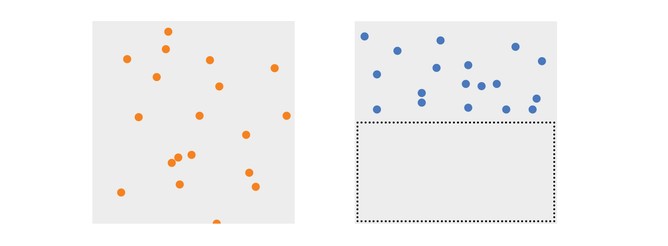
Tekdüze dağılımın mantığı şudur. Bir kümedeki noktaların konumuna bakarken, “Eğer yeterince çok sayıda nokta alırsam, bu noktalar alanın her köşesine adil biçimde dağılır mı?” diye sorarız. Eğer cevap evetse, o zaman noktalar tekdüze yani düzgün biçimde dağılmıştır.
Burada “yeterince çok sayıda nokta” önemlidir. Az sayıda noktayla ölçüm yaparsak, şansa bağlı olarak bazı bölgelerde fazla, bazılarında az nokta olur. Ama nokta sayısını artırdıkça, bu dengesizlik azalır.

Tekdüze dağılım, rastgeleliği ölçmek için yararlı olsa da oldukça yüzeysel bir yöntemdir. Noktaların ne kadar rastgele yerleştiğini anlamak için başka ölçütler de gerekir.
Aşağıdaki üç kutudaki noktalara bakalım. İlk bakışta hepsi düzgün dağılmış gibi görünür. Ama aralarında fark vardır. Soldaki kutuda noktalar neredeyse eşit aralıklarla dizilmiş, bu yüzden fazla düzenlidir. Ortadaki kutuda ise noktalar kümelenme eğilimi gösterir, yani bazı bölgelerde toplanmıştır. Yalnızca sağdaki kutudaki noktalar gerçekten rastgele görünür.
Bu tür gözlemler, matematikçileri daha gelişmiş testler geliştirmeye yöneltmiştir. Bunlardan biri “boşluk dağılımı” (gap distribution), diğeri ise “çift korelasyonu” (pair correlation) testidir. Boşluk dağılımı, noktalar arasındaki aralıkların büyüklüğünü ölçer.
Çift korelasyonu ise noktaların birbirine ne kadar yakın ya da uzak durduğunu, yani ne ölçüde kümelendiklerini inceler. Bu testlerde, giderek daha fazla noktayı hesaba katarak aralıkların veya yakın çiftlerin sayısı ölçülür.
Eğer bu ölçümler, tamamen rastgele bir dağılımdan beklenen değerlerle uyuşuyorsa, o zaman dağılım “Poisson tipi” olarak adlandırılır. Bu ad, olasılık teorisinin öncülerinden Fransız matematikçi Siméon-Denis Poisson’dan gelir.
Rastgele Sayılar Neden Önemlidir?
Sözde rastgele sayılar pek çok alanda karşımıza çıkar. Modelleme çalışmalarında, kumarhanelerde ve piyango sistemlerinde bu tür sayılar temel girdiler olarak kullanılır. Bankalar ve finans kurumları da güvenlik ve sahtecilik tespitinde bu sayılardan yararlanır.

Çünkü bilgisayar korsanları bu kodları kırmaya büyük ilgi gösterir, bu yüzden sözde rastgele sayılar üretmek için giderek daha karmaşık yöntemler geliştirilmiştir. Örneğin, birçok “rastgele sayı” üreteci fiziksel süreçlerden yararlanır. Siber güvenlik şirketi Cloudflare’in LavaRand sistemi buna ilginç bir örnektir. Bu sistem lav lambalarının hareketlerini kullanarak sözde rastgele sayılar üretir.
Sonuç olarak
Gerçek rastgelelik, özünde öngörülemezdir ve hiçbir örüntü barındırmaz. Radyoaktif bozunma ya da atmosferik olaylar bu tür rastgeleliğin doğadaki örnekleridir. Ancak bu düzeydeki öngörülemezliği hesaplamalı sistemlerde yeniden üretmek son derece zordur.
Rastgele sayı üretimi; matematik, bilgisayar bilimi ve kriptografinin kesişiminde yer alan çok yönlü bir araştırma alanıdır. Gerçek rastgelelik arayışı hem bilim insanlarını hem de meraklıları büyülemeye devam ederken, rastgele sayı üretiminin ardındaki ilkeleri anlamak, modern bilişim dünyasının karmaşıklıkları içinde güvenle ilerlememizi sağlar.
Kaynaklar ve ileri okumalar:
- Shaltiel, Ronen. (2011). An Introduction to Randomness Extractors. 21-41. 10.1007/978-3-642-22012-8_2.
- Kroese, Dirk & Brereton, Tim & Taimre, Thomas & Botev, Zdravko. (2014). Why the Monte Carlo method is so important today. Wiley Interdisciplinary Reviews: Computational Statistics. 6. 10.1002/wics.1314.
- These Numbers Look Random but Aren’t, Mathematicians Prove. Yayınlanma tarihi: 30 Ocak 2024. Kaynak site: Scientific American. Bağlantı: These Numbers Look Random but Aren’t, Mathematicians Prove
- Dorca Josa, Aleix. (2018). Identifying users using Keystroke Dynamics and contextual information.
Matematiksel





