Ramanujan Toplamı: 1+2+3+4+…= -1/12 Sonucu Nasıl Mümkün Olur?

Elinize bir hesap makinesi alın ve arka arkaya sayıları toplamaya başlayın. Sonuç olarak -1/12 bulmanız mümkün müdür?

Sonsuz sayıda matematikçi bir fırına girer. İlki bir ekmek ister. İkincisi yarım ekmek, üçüncüsü çeyrek ekmek, ardından sekizde bir ekmek derken siparişler giderek küçülür. Sonunda sabrı tükenen fırıncı iki ekmek çıkarır, tezgâha koyar ve şöyle der: “Siz matematikçilerin sınırlarınızı bilmesi gerekiyor!”

Bu küçük hikâye, matematikte önemli bir kavrama dayanır. Sonsuz sayıda girdiyi alıp tek bir sonuç üreten fonksiyonlar gerçekten vardır. Başka bir deyişle, sonsuz sayıda sayıyı topladığınız hâlde sonlu bir sonuç elde edebilirsiniz.

Örneğin tüm pozitif tam sayıları toplarsanız, sonuç kaçınılmaz olarak sonsuza gider. Sayılar büyüdükçe toplam da kontrolden çıkar. Matematikte buna ıraksaklık denir.

Ancak her sonsuz toplam böyle davranmaz. Eğer topladığınız terimler her adımda küçülüyorsa, toplam bazen belirli bir değere yaklaşır. Yani sonsuz sayıda terim, sonlu bir sonuca ulaşır. Bu duruma da yakınsaklık denir.

Burada dikkatli olmak gerekir. Terimlerin küçülmesi, toplamın mutlaka yakınsak olduğu anlamına gelmez. Matematiğin en meşhur karşı örneklerinden biri harmonik seridir.

$$1 + \frac{1}{2} + \frac{1}{3} + \frac{1}{4} + \cdots$$

Bu seride terimler sürekli küçülür; ama toplam hiçbir zaman belirli bir değere varmaz. Bu durum ilk kez 1300’lerde Nicole Oresme tarafından kanıtlanmıştır. Böylece, giderek küçülen sayıların yine de ıraksak bir toplam üretebileceği anlaşılmıştır.

Öte yandan, bir serinin yakınsak olduğunu bilmek, toplamını hesaplamayı kolaylaştırmaz. Matematikçiler, kare sayıların terslerinin toplamının yakınsak olduğunu biliyordu:

$$\frac{1}{1^2} + \frac{1}{2^2} + \frac{1}{3^2} + \cdots$$

Ama bu toplamın değerini kimse hesaplayamıyordu. 1644’te Pietro Mengoli bu soruyu ortaya attı. Problem, daha sonra Basel Problemi olarak anılacaktı. Onu çözen kişi, matematik tarihinin en büyük isimlerinden biri olan Euler oldu. 1735’te Euler, bu toplamın π² /6 ​olduğunu gösterdi. Ortada ne bir çember vardı ne de bir açı; ama π bir anda ortaya çıkmıştı.

Bernoulli Sayıları Nedir?

Sayı dizilerini toplamaya başladığınızda oldukça ilginç sonuçlarla karşılaşırsınız. Örneğin 1, 2, 3, 4, 5, … biçimindeki tam sayıların herhangi bir başlangıç dizisini topladığınızda, sonuç her zaman bir üçgen sayı olur. Tek sayıların dizisini topladığınızda da, elde edilen sonuç her zaman bir kare sayıdır.

Ancak bazen bu toplamları hesaplamak da kolay olmaz. Bu durumda ise bazı kestirme yollara başvurulur. Bu kestirmelerden birisi de İsviçreli matematikçi Jacob Bernoulli tarafından bize gösterilmiştir. İlk on beş küp sayının toplamını, 4’ün ilk elli kuvvetini ya da 13’ün ilk seksen yedi kuvvetini toplamak istiyorsanız, bunu yapabilen bir fonksiyon vardır. Bu fonksiyon aşağıdaki gibidir.

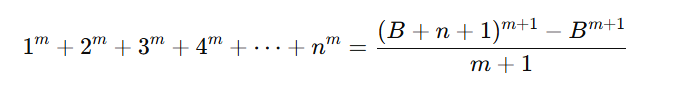
İlk $n$ sayının, her biri $m$. kuvvete yükseltilmiş hâllerinin toplamını bulmak istiyorsanız, bu değerleri Bernoulli’nin denklemine yerleştirmeniz yeterlidir. Denklem sonucu doğrudan verir. Ancak buradaki B harfi, bir değişken değildir.

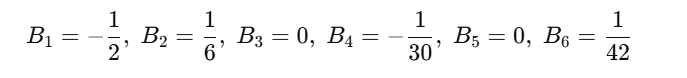
B ile cebirsel işlemler yapabilirsiniz; ancak iş kuvvet almaya geldiğinde kurallar bozulur. Burada $B^2$ ya da $B^3$, $B$’nin karesi ya da küpü anlamına gelmez. Bunun yerine, bu üstlü ifadeler Bernoulli sayıları adı verilen özel bir sayı dizisinin ilgili terimlerine karşılık gelir. Yani $B^2$ ve $B^3$, sırasıyla $B_2$​ ve $B_3$​ Bernoulli sayılarını temsil eder. Yukarıda ilk birkaç tanesini görebilirsiniz.

Eğer $m = 1$ değerini yerine koyarsanız, yani $1 + 2 + 3 + \cdots$ ifadesinin sonucunu bulmak isterseniz toplamak isterseniz, denklem bildiğimiz üçgen sayı formülüne indirgenir. Yani ilk $n$ tam sayının toplamını veren, hepimizin aşina olduğu n.(n+1) / 2 ifadesi elde edilir.

Ramanujan Toplamı Nedir?

Zaman içinde matematikçiler, Bernoulli sayılarını kullanarak sonsuz dizilerle ilgili bir numara keşfetti. Normalde, belli bir kuvvete sahip tüm tam sayıları toplarsanız, sonucun sonsuz olmasını beklersiniz. Ama matematikçiler doğrudan toplamak yerine, dolaylı bir yol izledi.

Önce, sayıların terslerinin toplamını veren bir formül kullandılar. Sonra bu formülü, kuvveti negatif bir değere taşıyacak şekilde genişlettiler. Bu yöntemle matematikçiler, doğrudan toplanması imkânsız görünen diziler için bile tutarlı ve şaşırtıcı sonuçlar elde edebildiler.

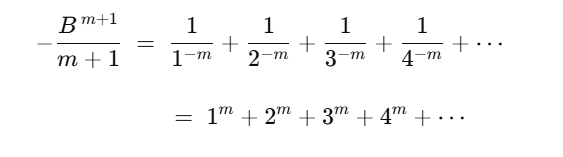
Yukarıdaki denklemde $m = 1$ değerini yerine koyalım. Bu, tüm pozitif tam sayıların toplamını vermelidir. Sezgimiz toplamın sonsuz olması gerektiğini söyler. Ancak Bernoulli sayıları şaşırtıcı bir sonuç ortaya koyar. Bu yaklaşıma göre toplam −1/12 olur.

Sonuç Olarak

Tüm sayıların toplamının $-1/12$ olması ilk bakışta akıl dışı gelir. Ancak daha dikkatli bir bakış, bu sonucun anlamsız olmaktan ziyade, sonsuz toplamların doğasına dair beklenmedik bir pencere açtığını düşündürür. Bugün bu yaklaşıma Ramanujan toplamı denir. Çünkü bu tür hesaplamalara Ramanujan’ın notlarında da rastlanır.

Elbette pozitif tam sayıların toplamı klasik anlamda sonsuzdur. Ancak bu sonsuzluğu bir an için kenara çekip, altta yatan yapıya bakmayı başarırsanız, geride şaşırtıcı bir şey kalır: o yapının içinde $-\frac{1}{12}$ gizlidir. Bu sayı, toplamın kendisi değil; sonsuzluğun arkasında kalan daha ince matematiksel bilginin bir yansımasıdır.

---

Kaynaklar ve ileri okumalar için:

• Rao, K. & Berghe, G.. (2005). On an entry of Ramanujan in his Notebooks: A nested roots expansion. Journal of Computational and Applied Mathematics – J COMPUT APPL MATH. 173. 371-378. 10.1016/j.cam.2004.04.009.
• Infinity or -1/12?; Yayınlanma tarihi: 18 Şubat 2014; Kaynak site: Plus math: Bağlantı:Infinity or -1/12?

---

Size Bir Mesajımız Var!

Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.

Matematiksel