1887-1920 yılları arasında yaşayan ve matematik konusunda dünya tarihine çok şey kazandıran Srinivasa Ramanujan adını pek çok şey vasıtası ile duymuş olabilirsiniz. Kendisi sonsuz serilere takıntılı bir dehaydı. Sayılarla oynamayı seviyordu. Bunun sonucunda da kısacık yaşantısından matematik tarihinden önemli bir iz bıraktı. Şaşırtıcı çıkarımlarından birisi de günümüzde Ramanujan Kökleri olarak biliniyor.
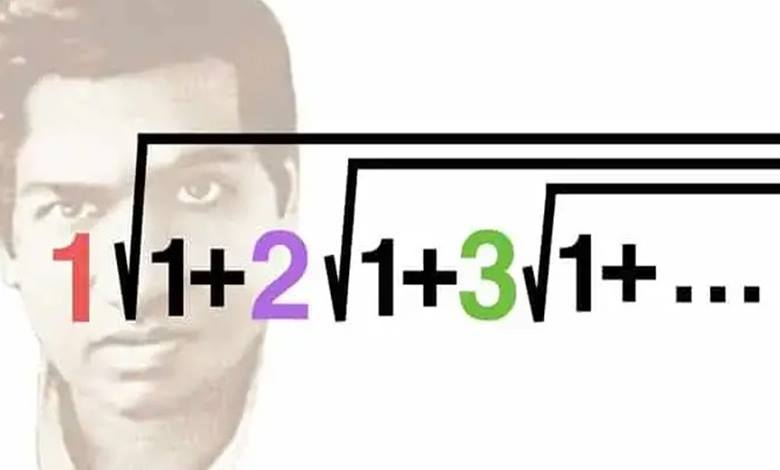
Ramanujan köklerine geçmeden önce onun beyninin nasıl çalıştığı hakkında fikir edinmenizi isteriz. Dediğimiz gibi sayılarla oynamayı seven bu genç adam ardından ilginç çıkarımlar ve formüller bırakmıştır. Örneğin sonsuz bir çarpım kullanarak üç ünlü sabit phi (altın oran), e (doğal logaritma temeli) ve π’yi birbirine bağlayan aşağıda gösterilen formül gibi ilginç matematiksel teoremler üretmiştir.
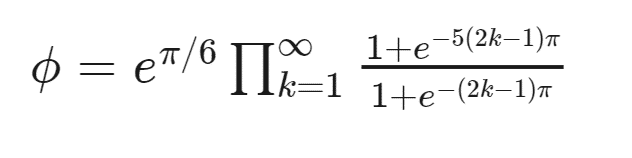
Ramanujan pi sayısının yaklaşık değerlerini hesaplamak için de yüzlerce formül geliştirmişti. Cambridge üniversitesine gelmeden önce yazdığı iki defterde 400 sayfa formül ve teorem bulunur. Ramanujan’ın formüllerinden çoğunun ne anlama geldiği yakın zamana kadar tam olarak anlaşılamadı.
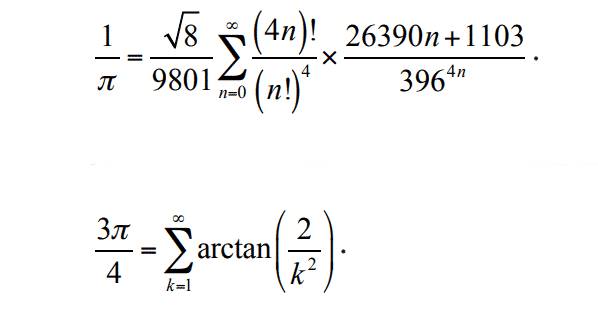
Ancak 1980’lerin ortalarında, pi sayısını hesaplamak için, Ramanujan’ın denklemlerini kullanabileceğimizi fark ettik. Örneğin yukarıdaki ilk formülün her terimi, pi sayısının 8 yeni basamağını hesaplamamızı sağlar. Bu sayede 1985 yılında pi sayısının 17 milyon basamağını hesaplamak mümkün oldu.
Ramanujan’ın Sonsuzluk Takıntısı Ve Ramanujan Kökleri

Çoğu matematikçi için bile uğraşması oldukça zaman alan bu gibi formüllerin yanı sıra Ramanujan sonsuz kökler ve sonsuz seriler ile de oynamayı severdi. 1911’de Hintli matematik dehası the Indian Mathematical Society’e aşağıdaki problemi yolladı. Kendisi bu problem ile matematik topluluğu içinde yer almaya çalışıyordu. Neyse ki birkaç yıl sonra G.H. ile iletişime geçecek ve tüm zamanların en verimli matematik ortaklıklarından birini kuracaklardı.
Kendisi kökler ile ilgili sorusuna birkaç ay boşuna cevap bekledikten sonra çözümü açıkladı. Bu makalede, Ramanujan’ın çözümünün basitleştirilmiş bir versiyonuna göz atacağız.
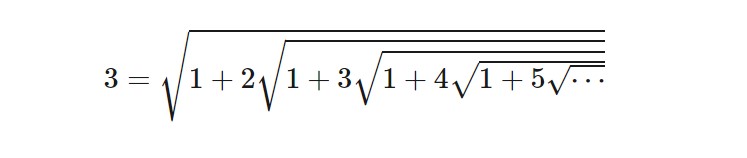
Yukarıdaki eşitliğe göz attığınız zaman sonucun 3 olması size ilginç gelecektir. Ramanujan bu eşitliğin sağ tarafını bir bulmaca olarak yayınlamış ve sonucun kaç çıktığını sormuştu. Sonrasında da cevabın 3 olduğunu açıklayacaktı. Şimdi gelin onun bu cevaba nasıl ulaştığını anlamaya çalışalım. Öncelikle negatif olmayan herhangi bir x reel sayısı için aşağıdaki özdeşliği yazmamız mümkündür.
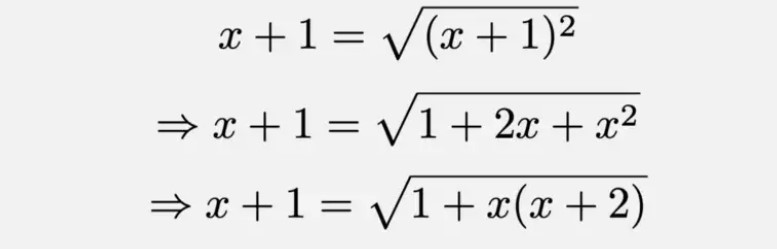
Şimdi yukarıdaki özdeşliği bir adım ileriye taşıyalım. Bu sefer de (x + 2) yerine ((x + 1) + 1) yazalım. Bu durumda özdeşliğimiz aşağıdaki gibi gözükecektir.
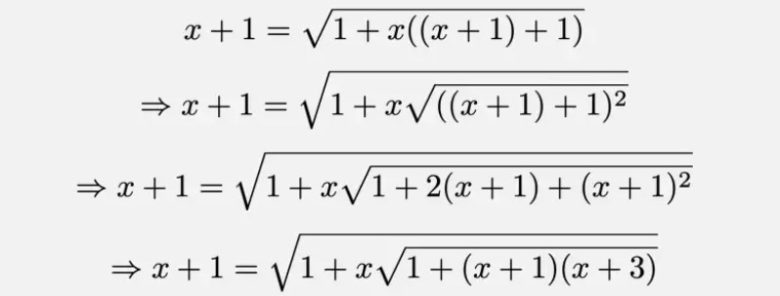
Madem başladık özdeşliğimizi geliştirmeye devam edelim. Muhtemel bu noktada Ramanujan kökleri ile ilgili kalıbı fark etmiş olmalısınız. Bu durumda şimdi yapmamız gereken (x + 3) ‘ü ((x + 2) + 1) biçiminde yazmak olacak. Artık özdeşlik aşağıdaki gibi gözükmektedir.
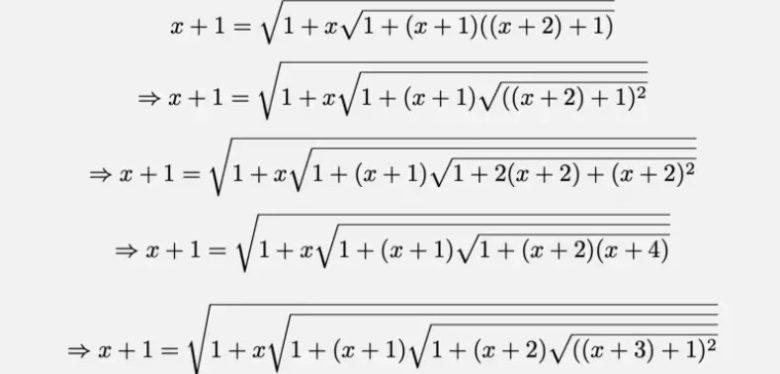
Böylece süreç özyinelemeli olarak sonsuza kadar gerçekleşecektir. Bu sonucun genel gösterimi de aşağıdaki gibi olacaktır.
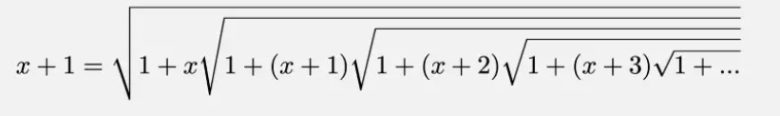
Artık elimizde genel bir denklem olduğuna göre şimdi x yerine istediğimiz bir sayıyı yazabiliriz. Orijinal sorunun cevabını elde etmek için x yerine 2 yerleştirmemiz gerekmektedir. Bu durumda sorumuzun cevabı aşağıda da gördüğünüz gibi basit bir biçimde 3 çıkacaktır.
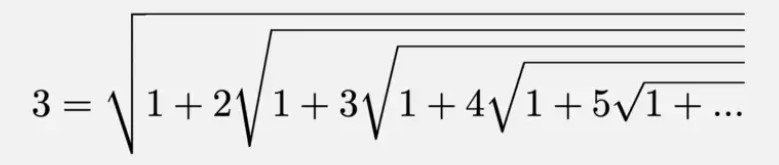
Ayrıca genel özdeşliği elde ettiğimiz için bu özdeşlik yardımı ile x yerine farklı sayılar yerleştirerek farklı sonuçlar da elde edebiliriz. Örneğin istersek x yerine 124 yerleştirip aşağıdaki sonuca da ulaşabiliriz. Kendi sonsuz iç içe geçmiş köklerinizi oluşturarak ilginç sonuçlar elde edebilirsiniz.
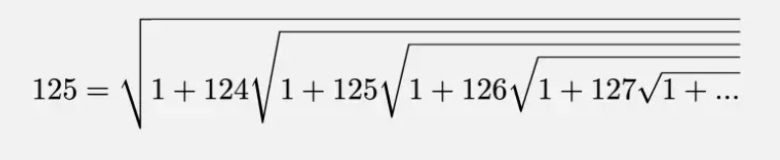
Ramanujan Köklerinin İspatı
Ramanujan yukardaki çözüm için herhangi bir ispat vermedi. Aslına bakarsanız Ramanujan hiçbir formülünün ispatını yapmadı. Ramanujan’ın çalışma biçimi buydu. Öncelikle bir yapı geliştiriyor, sonrasında da bu yapıya çeşitli sayılar yerleştirip bazı sonuçlar elde ediyordu.

Srinivasa Ramanujan on altı yaşındayken Synopsis of Elementary Results in Pure and Applied Mathematics (Soyut ve Uygulamalı Matematikte Temel Bilgiler Özeti) adındaki bir kitaba denk gelmişti. Kitap aslında bir ders kitabıydı ve ispatlara girilmeden binlerce sonuç, formül ve denklem içeriyordu. Kuramsal matematiği ilk kez bu kitaptan öğrenen Ramanujan’a hayatı boyunca belki de bu nedenle bir ispat yapma ihtiyacı duymadı.
Hayatının ikinci evresinde Cambridge’deki ünlü İngiliz matematikçi GH Hardy mentörlüğünde formal matematik eğitimi alsa da onun bizi etkileyen formüllerinden bir çoğu bu dönemden öncesine aittir. İşin ilginç tarafı günümüzde yeni yeni onun formüllerinin doğruluğu anlaşılabilmektedir.
Örneğin, karadeliklerin özelliklerini açıklamak için kullanılan ilk formüllerden bazılarını Srinivasa Ramanujan farkında olmadan geliştirmişti. Ancak elbette o zamanlarda kimsenin karadelikler hakkında bir fikri yoktu.
Kaynaklar ve ileri okumalar:
- Solution: ‘Puzzles Inspired by Ramanujan’; yayınlanma tarihi: 8 Ağustos 2016; Kaynak site: Quanta Magazine. Bağlantı: Solution: ‘Puzzles Inspired by Ramanujan’
- Different ways of looking at numbers; Yayınlanma tarihi: 1 Haziran 2000; Bağlantı: Different ways of looking at numbers/
- Ramanujan’s Nested Radical Problem. Yayınlanma tarihi: 29 Ağustos 2021; Bağlantı: https://www.cantorsparadise.com/
- Rao, K. & Berghe, G.. (2005). On an entry of Ramanujan in his Notebooks: A nested roots expansion. Journal of Computational and Applied Mathematics – J COMPUT APPL MATH. 173. 371-378. 10.1016/j.cam.2004.04.009.
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel






