Sıralama, bilgisayarların yaptığı en temel eylemdir. Aslında birçok yönden bilgisayarların yaratılma nedenidir. Sıralama denince de akla modası yıllardır geçmeyen Quicksort Algoritması gelecektir.

Çevrimiçi alışverişlerinizde bir şeyler satın alırken, genellikle aradığınız ürünleri fiyat, ortalama müşteri memnuniyet puanı veya belki de tarihe göre sipariş etme seçeneğine sahip olursunuz. Düşünürseniz alışveriş yaptığınız ortamda binlerce ürün vardır. Oysa ki bir sürü şeyi (örneğin rafınızdaki kitaplar) düzene koymayı denediyseniz, bunun zaman alacağını bilirsiniz. Bu nedenle dünya bir sıralama algoritması olan Quicksort algoritmasını icat ettiği için bilgisayar bilimcisi Tony Hoare’ye büyük bir şükran borçludur.
İşin ilginç olanı Hoare, Quicksort algoritmasını çevrimiçi alışveriş yapmayı düşünmeden, bu tip bir alışverişin henüz daha farkında olmadığımız zamanlarda geliştirdi. Ancak yine de onun geliştirdiği bu algoritma günümüzün en iyi sıralama algoritmalarından biri olarak kabul edilmektedir.
Quicksort Algoritması İle Nasıl Tanıştık?
Aşağıda bir örneğini gördüğünüz kabarcık sıralaması ( Bubble Sort) basit bir sıralama algoritmasıdır. Kabarcık sıralaması adını, tıpkı baloncukların yüzeye çıkması gibi listenizdeki şeylerin yavaş yavaş doğru yerlerine doğru hareket etmesinden alır. Arkasındaki fikir basittir. Karışık halde duran kitaplarınızı alfabetik bir şekilde sıralamak istediğinizi düşünün. Yapmanız gereken şey sıralı olmayan çiftleri aramak ve bunları düzenlemek olurdu. Sırası yanlış olan bir çift bulamadığınızda da işiniz biterdi.
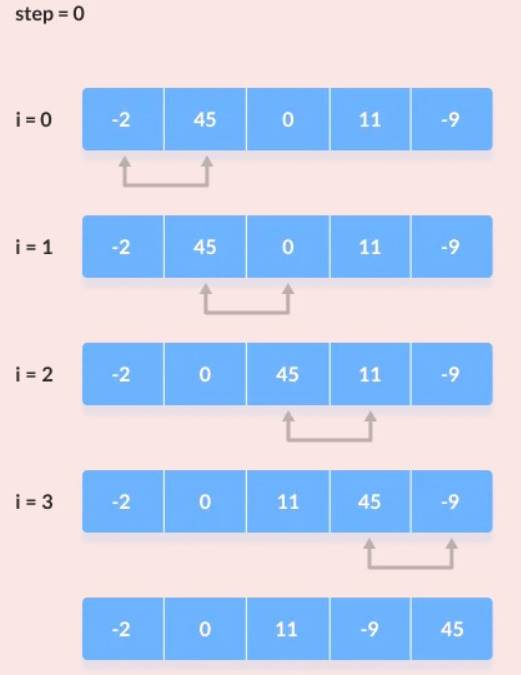
Bu algoritma da aynı mantıkla çalışır. Size bir sıraya konması gereken (örneğin sayılar) bir liste verildiğinde (örneğin artan sıralama), önce ilk iki öğeyi karşılaştırır ve doğru sırada değilse bunları değiştirirsiniz. Sonrasında ise sahip olduğunuz listede, ikinci ve üçüncü şeye bakar ve yanlış sıradaysa bunları değiştirirsiniz. Listenizin sonuna ulaşana kadar listede üçüncü ve dördüncü sırada, listede dördüncü ve beşinci sıradakileri aynı biçimde değiştirmeye devam edersiniz.
Bu işlem sırasında hiçbir şeyi değiştirmek zorunda kalmadıysanız işiniz tamamdır. Bu, listenin zaten doğru sırada olduğu anlamına gelir. Bunun sonucunda da artık durmanız gerekecektir. Ancak en az bir çifti değiştirmek zorunda kaldıysanız, aynı işlemi listenin başından itibaren yeniden başlatırsınız. Sonunda listeniz sıralanacaktır.

Sizin de fark edeceğiniz gibi fikir basit ama çok da etkili değildir. Sizin ( daha doğrusu algoritmanın çalıştığı bilgisayarın) bir listenin tamamının sıralanması için gereken zaman, listenin uzunluğu ile ilişkilidir. Tony Hoare’nın işin içine girdiği yerde burasıdır. Bubble Sort algoritmasını daha verimli kılmak için yaptığı çalışmalar sonucunda, Quicksort algoritması doğacaktı.
Quicksort Yani Hızlı Sıralama Algoritması Nasıl Çalışır?
Bu algoritma, az önce anlattığımız sıralama algoritması kadar basit olmasa da arka planındaki fikir güzel ve zariftir. Diyelim ki elimizde artan biçimde sıraya konması gereken bir sayılar listesi var. Böyle bir sayı listesi verildiğinde, önce listenizden bir sayı seçersiniz. Buna pivot sayı denir. Sonrasında da listedeki diğer tüm sayıları bu sayıyla karşılaştırırsınız.
Genel fikir, tüm sayıları kontrol etmek ve pivottan daha küçüklerse, artan sırada dizdiğimiz için, pivotun önüne taşımaktır. Aşağıdaki örnekte pivot sayımız yedidir. Bu mantıkla düzenledikten sonra yedi sayısının sol tarafındakiler daha küçük, sağ tarafındakiler ise daha büyük olacaktır.
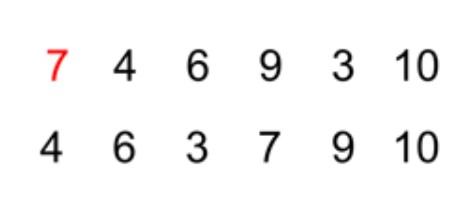
Ancak sizin de fark ettiğiniz gibi sayılar hala düzenli değil. Bu durumda, aynı işlemi listenin daha küçük kısmına ve daha büyük kısmına ayrı ayrı uygulamanız gerekecektir. Yani önce yediden küçükler için bir pivot sayı seçersiniz ve ona göre sıralarsınız. Sonrasında da aynı işlemi yediden büyükler için de yaparsınız. Aşağıdaki örnekte bunun için 4 ve 9 seçilmiştir. Bu işlemin sonucunda sayı diziniz sıralanmış olur.

Hoare’nin Hızlı Sıralama Algoritması İçin Harika Fikri
Ancak bilgisayar konusunda deneyimliyseniz, bu sıralamanın aslında küçükler ve büyükler biçiminde iki liste oluşturduğunuz ve bir bilgisayarın çalışma verimliliğini düşürdüğünü fark edeceksiniz. Bunun için bu bölünmeyi ek listelere ihtiyaç duymadan yapmak gerekir. Neyse ki Hoare’nin bunun için de harika bir fikri vardı.
Şimdi yine bir sayı dizisi düşünün ve bir sayıyı pivot olarak seçin. Bu sefer sol işaret parmağınızı pivotun sağındaki sayıya (ikinci sayı) ve sağ işaret parmağınızı son sayıya koyduğunuzu hayal edin. Amacınız pivota göre yanlış sırada olan sayı çiftlerini bulmak olacaktır. Sonrasında da listeyi hem soldan hem de sağdan tarayarak yerlerini değiştirmeniz gerekecektir.
Şimdi aşağıdaki görsele balın. L harfi sol, R harfi de sağ işaret parmağınızı gösteriyor. Bu aşamada pivot sayımızdan yani 7 sayısından, daha büyük sayıları arıyoruz. Sol taraftaki sayı yani 4, pivot sayımız yani 7’den küçük. Bu durumda sol parmağınızı bir sayı sağa doğru kaydırın. Şimdi 6 sayısındasınız. Yine küçük. Bir kere daha sağa kaydırın. Bir sonraki sayı ise 9. Şimdi durun.
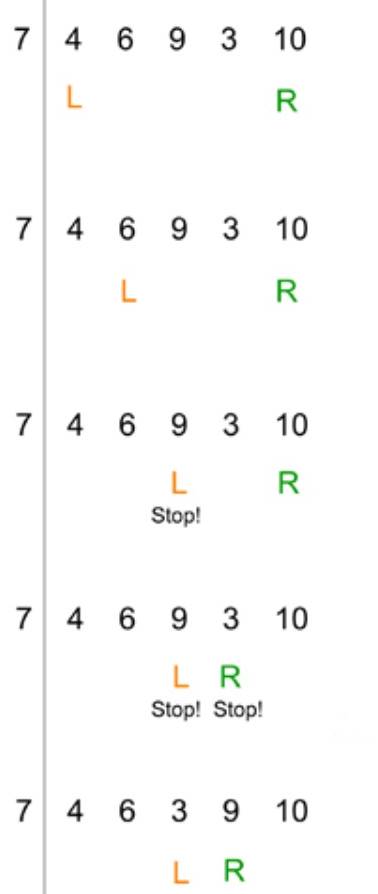
Sırada sağ parmağınız var. Buradaki sayı 10. Pivot sayımız olan 7’den daha küçük olanlara bakalım. 10 sayısı olmadı, bu durumda parmağınızı bir sayı sola kaydırın ve 3 sayısın da durun. Her iki parmağınız durduğunda, pivota göre yanlış sırada olan iki sayı belirlediniz. Şimdi bu sayıların yani 3 ile 9 sayısının yerlerini değiştirin.
Bu işlemin birkaç tekrarından sonra her iki parmak da durduğunda sıralamamız tamamlanır. Pivot, listedeki en küçük veya en büyük sayı olduğunda, tanımladığımız algoritmanın başının belaya girebileceğini unutmamalıyız. Ancak bununla başa çıkmanın da yolları vardır. Ancak bu yazının içinde kısa sürede tanımlayamayacağımız kadar karmaşıktır. Yine de merak ederseniz ayrıntılar için Wikipedia’ya bakın.
Sonuç Olarak;
Bu yazımızda en basit hali ile Quicksort yani Hızlı Sıralama algoritmasının çalışma mantığını en basit hali ile aktarmaya çalıştık. Elbette konu hakkında bilginizi geliştirmek için ek kaynaklardan öğrenmeye devam etmeniz gerekecektir. Bunun için aşağıdaki kaynaklar kısmımıza göz atabilirsiniz.
Ayrıca algoritmalar hakkında öğrenmeye devam etmek istiyorsanız Çalışma Kağıtlarını Ve Gardırobunuzu Düzenlemek İçin En İyi Algoritma Nedir? başlıklı yazımıza da göz atmanızı öneririz.
Kaynaklar ve ileri okumalar
- Happy birthday Quicksort: Starting with bubbles. Yayınlanma tarihi: 4 Haziran 2021; Bağlantı: Happy birthday Quicksort: Starting with bubbles./
- Happy birthday Quicksort! Yayınlanma tarihi: 4 Haziran 2021; Bağlantı: https://plus.maths.org/
- Quick Sort; bağlantı: https://www.geeksforgeeks.org/quick-sort/
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel