Belirli bir süre içinde bir olayın ne sıklıkla gerçekleşeceğini tahmin etmek istiyorsanız ve bu olay nadirse, adını Fransız matematikçi Siméon Denis Poisson’dan (1781–1840) alan Poisson dağılımı bu tahmin için uygun bir yöntemdir.

Futbolda goller, bir maçın tamamı düşünüldüğünde görece nadir gerçekleşen olaylardır. Bu özellik, Poisson dağılımını futbol analizleri için özellikle uygun kılar. Dağılım, geçmiş maç verileri ve takımların ortalama gol oranları kullanılarak bir karşılaşmada kaç gol atılabileceğini incelemek ve öngörmek için pratik bir araç sunar.
Örneğin, maç başına ortalama 1.6 gol atan bir takımla maç başına ortalama 1.2 gol atan başka bir takımın karşılaştığını düşünelim. Poisson dağılımı, bu maçta ortaya çıkacak farklı skorların olasılıklarını hesaplamaya imkân verir.
Bu yöntemle, golsüz beraberlikten 1–1’lik skora, iki takımdan birinin galibiyetine ya da daha farklı sonuçlara kadar her olası skor için olasılıklar tahmin edilebilir. Tüm bu hesaplamalar, takımların uzun vadeli ortalama gol oranlarına dayanır.
Genel olarak Poisson formülü, ortalama gerçekleşme sıklığı bilinen olaylar için, belirli sayıda olayın ortaya çıkma olasılığını hesaplamayı sağlar ve ilgilenilen sonuca doğrudan bir olasılık değeri atar.

Poisson Dağılımı Nasıl Nedir Ve Nasıl Hesaplanır?
Olasılık dağılımları, sonucu önceden kesin olarak bilinemeyen ve birden fazla olasılığa sahip süreçleri tanımlamamızı sağlar. Her olasılık dağılımı farklı bir amaca hizmet eder ve farklı veri üretim mekanizmalarını temsil eder.
Poisson dağılımı da bu dağılımlardan biridir. Poisson dağılımının doğruluğu ve uygulanabilirliği birkaç temel varsayıma dayanır.
- Birincisi, olayların bağımsız olmasıdır. Her olay diğerlerinden bağımsız gerçekleşir. Bir olayın meydana gelmesi, başka bir olayın olasılığını etkilemez.
- İkincisi, ortalama hızın sabit olmasıdır. Olayların belirli bir zaman ya da mekân birimi başına ortalama gerçekleşme sayısı değişmez. İncelenen süre boyunca bu ortalama tutarlı kalır.
- Üçüncüsü, olayların rastlantısal biçimde ortaya çıkmasıdır. Herhangi bir düzen yoktur. Bu rastlantısallık, Poisson modelinin doğru sonuçlar vermesi için kritik önemdedir.
- Dördüncüsü, olayların ayrık ve sayılabilir olmasıdır. Örneğin bir günde alınan e-posta sayısı ya da gibi.
Bu varsayımları anlamak, Poisson dağılımını doğru biçimde uygulamak açısından hayati öneme sahiptir. Dağılım, bu koşulların sağlandığı durumlarda en etkili sonuçları verir.
Yılda gözlemlenen meteor yağmuru sayısını modellemek, bir ormanda nadir bir kuşun kaç kez görüldüğünü saymak ya da bir saat içinde bir gişeden geçen araç sayısını tahmin etmek buna örnektir. Hatta gelecek hafta bir at tarafından tekmelenme olasılığınızı tahmin etmekte bile işe yarar.
Poisson Dağılımı Ne İşimize Yarayacaktır?
Poisson dağılımının tarihsel bir olayı incelemek için kullanıldığı 19. yüzyıla geri gidelim. O dönemde araştırmacılar, Prusya ordusundaki farklı süvari birliklerinde görev yapan subayların, 20 yıl boyunca atlar tarafından tekmelenerek ölme sayısını anlamaya çalışıyordu. Bu tür ölümler nadirdi. Ancak soru şuydu: Bu olaylar gerçekten rastlantısal mıydı, yoksa altında yatan başka etkenler mi vardı?
Bu soruya iktisatçı ve istatistikçi Ladislaus Bortkiewicz yanıt aradı. Bortkiewicz, 14 kolordudan 20 yıla yayılan verileri topladı ve her bir kolordu için yıllık ölüm sayılarını inceledi. Poisson dağılımının formülünü kullanarak, belirli zaman aralıklarında bu tür ölümlerin kaç kez gerçekleşmesini beklemek gerektiğini hesapladı.
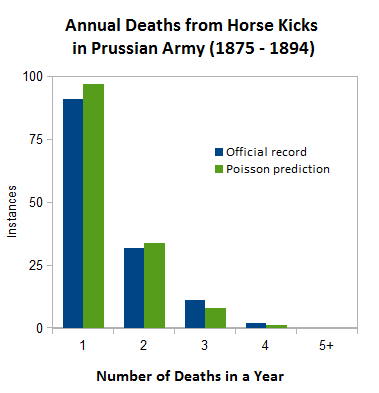
Hesaplanan değerler, gözlenen verilerle oldukça iyi uyuştu. Bu uyum, ölümlerin rastlantısal olaylar olduğunu ve ardında gizli bir neden bulunmadığını gösterdi. Bu çalışma, Poisson dağılımının gerçek dünyadaki olayları modellemek için nasıl kullanılabileceğine dair klasik bir örnektir.
Poisson dağılımının pratik uygulamaları, tarihsel olaylar ve spor analizlerinin çok ötesine uzanır. Aşağıda öne çıkan bazı uygulama alanları yer alıyor.
Konut Satışları ve İş Planlaması
Yerel bir emlak danışmanı olduğunuzu düşünün. Belirli bir zaman diliminde kaç konut satacağınızı öngörmek, iş planlaması ve tahminler açısından kritik önemdedir. Poisson dağılımı, geçmiş satış verileri ve ortalama satış hızları kullanılarak, bir gün, bir hafta ya da başka bir zaman aralığında kaç konut satılabileceğinin olasılığını tahmin etmeyi sağlar.
Hastalık Yayılımı ve Epidemiyoloji
Epidemiyoloji alanında Poisson dağılımı, bulaşıcı hastalıkların yayılmasını anlamada önemli bir rol oynar. Geçmiş veriler ve ortalama enfeksiyon hızları dikkate alınarak, salgınların ortaya çıkma olasılığı ve zaman içindeki seyri tahmin edilebilir. Bu analizler, halk sağlığı önlemlerinin planlanmasında temel bir araçtır.
Telekomünikasyon ve Ağ Trafiği
Poisson dağılımı, telekomünikasyon sistemleri ve ağ trafiğinin analizinde yaygın biçimde kullanılır. Çağrıların ya da veri paketlerinin geliş düzeni bu dağılımla incelendiğinde, şirketler ağ talebini daha iyi anlar.
Kalite Kontrol ve Üretim Süreçleri
Üretim ortamlarında Poisson dağılımı, özellikle kalite kontrolde kullanılır. Belirli bir süre içinde ortaya çıkan hatalı ürün sayısı bu dağılım yardımıyla analiz edilerek, kusur olasılıkları hesaplanır.. Bu yaklaşım, sorunlu noktaların belirlenmesine ve ürün kalitesinin artırılmasına katkı sağlar.
Trafik Kazaları ve Yol Güvenliği
Poisson dağılımının uygulandığı bir diğer alan trafik kazalarıdır. Geçmiş kaza verileri incelenerek, konum ve yol koşulları gibi etkenlere bağlı kaza oranları modellenebilir. Bu tür analizler, kazaları azaltmaya yönelik hedefli önlemler geliştirilmesine ve yol güvenliğinin artırılmasına yardımcı olur.
Poisson dağılımı, güçlü bir istatistiksel araçtır. Olasılıklara dayanarak anlamlı tahminler yapmamıza ve daha bilinçli kararlar almamıza imkân tanır. Poisson dağılımının ilkelerini hayatımızın çeşitli alanlarını iyileştirmek için değerlendirebiliriz.
Kaynaklar ve ileri okumalar:
- Maths in a minute: The Poisson distribution. yayınlanma tarihi: 7 Ocak 2022. Kaynak site: Plus Math. Bağlantı: Maths in a minute: The Poisson distribution/





