Matematikçiler Pi sayısını hesaplamak için sonsuz serileri kullanırlar. Örneğin günümüzde Bailey Borwein Plouffe formülü sayesinde, Pi sayısının basamaklarını hesaplamadan, istenilen herhangi bir basamağı bulabiliyoruz. Ancak biz bu yazıda konuya biraz daha eğlenceli bir bakış açısı ile yaklaşmaya çalışacağız.

Daha çok sınıfta öğrencilerimiz ile ya da evde çocuklarımız ile pi sayısını hesaplamak için kullanabileceğiniz bazı deneysel yöntemler aktaracağız. Ancak unutmayın. Sonucunda pi irrasyonel bir sayı olduğundan bu yöntemlerin hiç biri onun tam değerini bize veremez. Hazırsanız başlayalım
1. Tartarak Pi Sayısı Hesaplama
Öncelikle kare biçiminde bir karton alın ve bunu hassas terazide tartın. Ardından kartonunu üzerine bir çember çizin. Bu çemberin merkezi ile karenin merkezi çakışmalıdır. Çizdiğiniz çemberin adı iç teğet çemberdir.
Şimdi bu çemberi kesin. Sonra da tartın. Şimdi ilk bulduğunuz tartım sonucu ile şimdiki bulduğunuz sonucu birbirine bölün. Son olarak bulduğunuz sonucu dörtle çarpın. Elde ettiğini sonuç size yaklaşık olarak pi sayısını verecektir.
Bu noktada neden sorusunu sorabilirsiniz. Bir nesnenin ağırlığı ile alanı birbiri ile orantılıdır. Karenin bir kenarı a uzunluğunda olsun. Karenin alanı a2 ve dairenin alanı π (a/2)2 biçimindedir. İki alanı birbirine bölerseniz π/4 sonucunu elde edersiniz. Sonucu 4 ile çarpınca da pi sayısını yaklaşık olarak hesaplamış olursunuz.
Bu yöntem çok hassas bir yöntem olmasa da dikkatli bir şekilde uygularsanız pi sayısının ilk iki basamağını hesaplayabilirsiniz. Yani bulacağınız değer 3,1 ile 3,2 arasında bir yerlerde olacaktır. Elbette kartonu büyük alırsanız ve kesme işini düzgün yaparsanız, yüzde birler basamağına kadar doğru bir değer bulabilirsiniz. Ancak muhtemelen bunu yapmaktan daha eğlenceli bir yöntem bulabilirsiniz.
2. Noktalama Yöntemiyle Hesaplama Yapalım
Aslında bu yöntem biraz önce aktardığımız yönteme oldukça benziyor. Sadece alternatif bir bakış açısı sunuyor. Şimdi bir kare çizin ve içini bol sayıda nokta ile doldurun. Bu noktaların sayısına K diyelim. Az evvel aktardığımız biçimde karenin iç teğet çemberini çizin.
Çemberin iç kısmında yer alan noktaların sayısına da D diyelim. Son olarak iki sayıyı birbirine bölün ve çıkan bölümü 4 ile çarpın. Az evvel de aktardığımız neden ile bir kere daha pi sayısının yaklaşık değerini hesaplamış oluyorsunuz. Aşağıda bir örneği görebilirsiniz.

Ancak bu metodu kullanırken dikkat edilmesi gereken iki önemli durum mevcuttur. Bunlardan ilki noktalama rastgele yapılmadığı takdirde yapılan tahmin tutarsız olacaktır. İkincisi de nokta sayısı az olursa düzgün bir dağılım elde edilemeyecektir. Bunun devamında da doğru sonuca yaklaşmak pek mümkün olmayacaktır. Nokta sayısı arttıkça yaklaşımın doğruluğu artacaktır.
3. Dart Atışı Yaparak da Pi Sayısını Hesaplamak Mümkün
Yukarıda aktardığımız iki örnek size ilginç gelmedi ise bu sefer de işin içine biraz oyun katalım. Dışı kare ve içi daire biçiminde bir dart tahtası alın ve buna bir sürü atış yapın. İşimiz bir kere daha karenin içindeki tüm dart delikleri ile dairenin içindeki dart deliklerini saymak olacak.

Bundan sonrasında ne yapacağınızı ve nedenini artık biliyorsunuz. Takip edeceğiniz basamaklar yukarıdaki ilk iki örneğimiz ile yanı olacak. Sonrasında da bulduğunuz iki sayıyı birbirine bölün ve çıkan sonucu dört ile çarpın. Bir kere daha pi sayısının yaklaşık değerini, bir iki basamak olsa bile, bulmuş oldunuz.
4. Düğmeleri Çember Şeklinde Dizerek Pi Sayısını Hesaplayalım:
Şimdi biraz yöntemimizi değiştirelim. Düğmeler, bilyeler ya da taşlar dizerek de pi sayısını hesaplamak mümkündür.
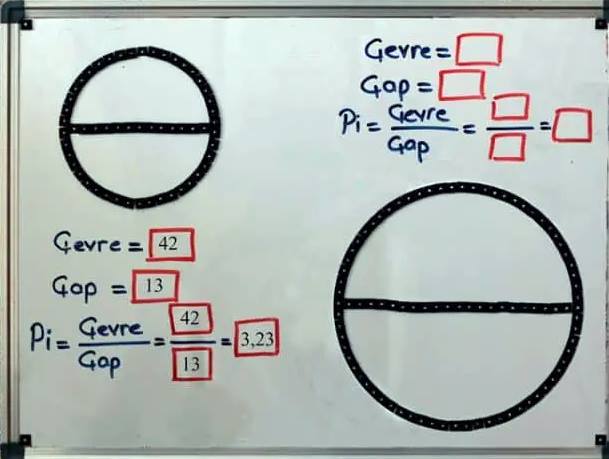
Bu yöntem için önce bir çember çizmelisiniz. Şimdi bu çemberin etrafını düğmelerle çevirin. Çemberin etrafına Ç tane nesne dizilebildiğini farz edelim. Şimdi, çemberin çapına da aynı nesneleri dizin. Bu çapı boyunca kaç nesne dizebildiğinizi de sayın. Buna da R diyelim. Ç’yi R’ye böldüğünüzde pi sayısını yaklaşık olarak elde edersiniz.
Bu yöntemde pi sayısının tanımından yararlanıyoruz. Çemberin etrafına dizebildiğiniz nesnelerin sayısı, çemberin çevresi ile; çap boyunca dizebildiğiniz nesnelerin sayısı da çapıyla orantılıdır. Bu durumda Ç/R sayısı bize pi’yi verecek, çünkü zaten Pi sayısının tanımı da budur.
5. Orta Saha Çemberini Adımlayarak da Pi Sayısını Bulabiliriz
Bir futbol sahasına gidin ve orta saha çemberinin etrafının kaç adım olduğunu bulun. (Ç adım olsun.) Şimdi, çemberin çapını da adımlayın ve bu sayıya R deyin. Ç/R oranı bize pi sayısının yaklaşık değerini verir. Buradaki mantık 4. yöntemdeki mantıkla tamamen aynı. Bu yüzden bir kez daha açıklamaya gerek duymuyoruz.
6. Sarkaç Yardımı İle Pi Sayısını Hesaplayalım

Uzunluğu yerçekimi ivmesinin (g) dörtte biri kadar (yani 245cm) olan bir ipin ucuna ağırlık bağlayıp sallayın. Bu sarkacın bir tam salınım yapması pi saniye sürecektir. Bir sarkacın periyodunu saniye cinsinden veren formül aşağıdaki gibidir.
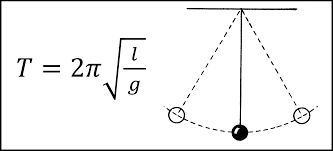
Burada T saniye cinsinden periyot, L sarkacın uzunluğu ve g de değeri yaklaşık olarak 9,8 m/sn² olan yerçekim ivmesidir. Eğer L=g/4 alırsak, bütün terimler sadeleşir ve sonuç pi saniye çıkar. (Periyot, sarkacın bir tam salınım yapması için geçen süredir.)
7. Kibrit Çöplerini Dökerek Hesaplamak
Bir zeminin uzun, ince ahşap çubuklarla döşeli olduğunu, elinizde bir iğne olduğunu ve iğnenin uzunluğunun ahşap çubukların genişliğine eşit olduğunu düşünün. İğneyi zemine atın. İğnenin, çubukları birbirinden ayıran çizgilerle kesişme olasılığı nedir? Okuduğunuz bu soru Buffon İğne Deneyi olarak bilinmektedir.

Buffon’un iğne probleminin beklenmedik bir cevabı vardır: Bu olasılık 2/π veya yaklaşık olarak %64’tür. Ortada herhangi bir çember yokken pi sayısının karşımıza neden çıktığını merak edebilirsiniz. Buffon, cevabını, sikloit adı verilen bir eğri altındaki alanı da kullanarak biraz karmaşık bir şekilde bulmuştu. Buffon iğne deneyi Monte Carlo yöntemine de benzer.
8- Monte Carlo Yöntemi
Bu yöntem de oldukça basittir ve aslında yukardaki örneklerimizin hepsinin çıkış noktasıdır. Öncelikle aşağıdaki görselde gördüğünüz gibi bir kare ve karenin kenarlarına teğet bir iç çember çiziniz.
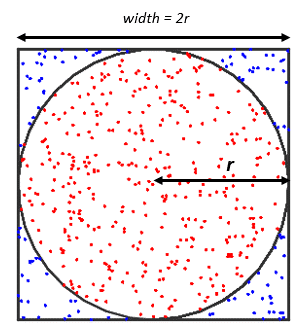
Karenin kenarlarının uzunluğunun 2 olduğunu, dolayısıyla alanının 4 olduğunu düşünün; dolayısıyla dairenin çapı 2, alanı ise pi’dir. Alanları arasındaki oran pi/4 veya yaklaşık 0,7854’tür. Şimdi bir kalem alın, gözlerinizi kapatın ve karenin üzerine rastgele noktalar koyun. Bunu yeterli sayıda yaparsanız ve çabalarınız gerçekten rastgeleyse, sonunda noktanızın dairenin içine düşme yüzdesi %78,54’e veya 0,7854’e yaklaşacaktır. Artık çağlar boyunca pi’yi hesaplayan matematikçiler arasına katıldınız.
Kaynaklar ve ileri okumalar:
- Buffon’s Needle Problem; https://mathworld.wolfram.com/
- Calculating pi with a pendulum; Bağlantı: https://www.youtube.com/
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel