Bugün ulaştığımız uygarlık seviyesinde Pisagor’un rolünü inkar etmek mümkün değil. Ancak elbette, onun en önemli ve evrensel mirası, adıyla özdeşleşmiş olan Pisagor Teoremidir.

Bu teorem, yalnızca matematiksel bir ilişkiyi ifade etmekle kalmaz; aynı zamanda geometri ile cebir arasında köprü kurar. “Bir dik üçgende, hipotenüsün karesi, diğer iki kenarın karelerinin toplamına eşittir” şeklinde basitçe ifade edilen bu ilişki, hem antik dünyada hem de modern matematikte hayati bir öneme sahiptir.
Bu teorem, geometride temel bir ilişkiyi açıklar: Bir dik üçgende, hipotenüsün (dik açının karşısındaki kenar) karesi, diğer iki kenarın karelerinin toplamına eşittir. Bu ilişki a2 + b2 = c2 biçiminde gösterilir.
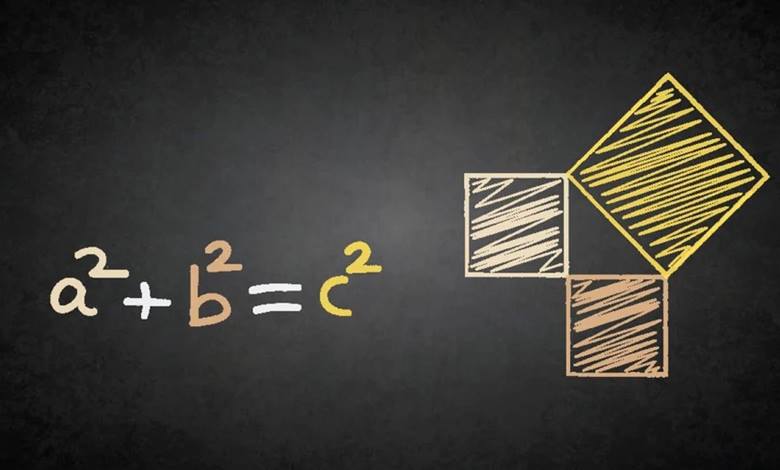
Pisagor Teoremini Kim Buldu?
Teorem, M.Ö. 6. yüzyılda yaşamış antik Yunan filozofu Pisagor ile ilişkilendirilse de, kökenleri çok daha eskiye dayanır. Kanıtlar, M.Ö. yaklaşık 1800’lerde Babillilerin bu ilişkiyi bildiklerini göstermektedir. Plimpton 322 gibi kil tabletler, Pisagor üçlüleri (teoremi sağlayan tam sayı setleri) içerir ve Babillilerin teoremi anladıklarını ve belki de arazi ölçümünde pratik olarak kullandıklarını işaret eder.

Benzer şekilde, antik Mısırlılar da teoremin bir çeşidini piramitlerin inşasında, özellikle mükemmel dik açılar oluşturmak için, 3-4-5 üçgenini kullanarak uygulamışlardır. Mısırlılar, bu tür üçgenleri oluşturmak için düğümlerle belirlenmiş uzunluklara sahip 12 birimlik ipler kullanmışlardı. Bu iplerle de, kenar uzunlukları 3:4:5 oranında olan dik üçgenler yapabiliyorlardı. İp germe mirasından dolayı, 3:4:5 oranındaki dik üçgen Mısır üçgeni olarak da bilinir.

Pisagor Teoreminin İspatları Nelerdir?
Pisagor Teoreminin bilinen ispatlarının sayısı, matematik tarihinde çok geniş bir yer kaplamıştır ve bugün bu teoremin yüzlerce farklı ispatı bulunmaktadır. Matematikçiler, tarih boyunca farklı bakış açılarıyla ve çeşitli yöntemlerle bu teoremi kanıtlamışlardır. Şu anda bilinen ispat sayısı yaklaşık 400’ü aşmıştır.

Pisagor Teoreminin bu kadar çok ispatının bulunmasının birkaç temel nedeni vardır. Öncelikle teorem, geometri ile cebir arasında doğrudan bir köprü kurduğu için, hem somut hem soyut matematikte farklı yollarla ifade edilebilir. Ayrıca, basit formülü, onu birçok farklı yöntemle test etmeye ve kanıtlamaya elverişli hale getirir.
Amerikalı matematikçi Elisha Scott Loomis, matematiğin farklı alanlarında pek çok eser kaleme almıştır. Ancak bunlar arasında en dikkat çeken, iki bölüm halinde yayınladığı “The Pythagorean Proposition” adlı kitabıdır. Bu eser, matematik tarihine damgasını vuran kapsamlı bir çalışma olarak bilinmektedir. Kitapta, Pisagor Teoremi için toplam 370 farklı ispat yer almaktadır. Bu ispatlardan üçünü aşağıda görebilirsiniz.

Dokümanlara dayanılarak bilinen ilk tam geometrik çözümün, Öklid tarafından verildiğini kabul etmek durumundayız. Bütün klâsik geometri kitaplarında bugün, tarihi değeri bakımından, sadece onun verdiği çözüm öğretilmektedir.

Pisagor ve takipçileri, teoremi sistematik bir şekilde kanıtlayarak, onu pratik bir gözlemden matematiksel bir teoriye dönüştüren kişilerdir. Teorem, matematiğin temel taşlarından biri haline gelen Öklid’in Elementler adlı eserinde de yer alarak matematik tarihinde kalıcı bir yer edinmiştir. Öklid’in ispatı, geometrik bir yaklaşımla, dik üçgendeki karelerin alanlarını kullanarak teoremi açıklar.
Pisagor Teoremini Trigonometri Kullanarak İspatlamak Mümkün mü?
2024 yılının ortalarında, iki lise öğrencisi, Pisagor Teoremini bir 20. yüzyıl matematikçisinin “imkansız” olarak nitelendirdiği bir yöntemle, trigonometri kullanarak ispatladı. Eğer bu ispat doğrulanırsa, 1927’de yayınlanan The Pythagorean Proposition adlı kitabında, Elisha Loomis tarafından dile getirilen, “trigonometri kullanılarak yapılan bir Pisagor Teoremi ispatı doğru olamaz” iddiasını çürütecek.
Elisha Loomis, Pisagor Teoremini ispat etmek için trigonometri kullanmanın, başlangıçta zaten teoremi varsaymayı gerektirdiğine inanıyordu. Bu, matematikte “dairesel mantık” olarak bilinen ve büyük bir hata sayılan bir argüman türüdür. Ona göre, trigonometri kullanılarak yapılan herhangi bir ispat, Pisagor Teoremi’ni kanıtlamak yerine dolaylı olarak varsaymış olurdu.
Ancak bu durum her zaman geçerli değildir. Gençlerin ortaya koydukları son ispat, Sinüs teoremini temel alıyor. Calcea Johnson ve Ne’Kiya Jackson’ın trigonometri kullanarak Pisagor Teoremini ispatlaması, matematik dünyasında heyecan uyandırdı. Eğer çalışmaları doğrulanırsa, bu yalnızca Loomis’in görüşünü çürütmekle kalmayacak, aynı zamanda gençlerin matematikteki yaratıcı potansiyelini gözler önüne serecek.
Pisagor Teoremi Günümüzde Ne İşe Yarar?
Günlük hayatta, Pisagor Teoremi çeşitli alanlarda farkında olmadan hayatımıza yön verir. İnsanlar bu teoremi en basit ve yaygın şekilde inşaat ve marangozluk işlerinde kullanır. Örneğin, bir zemin planı tasarlarken, bir dik üçgenin iki kenarını bilerek çapraz mesafeyi hesaplar ve yapının doğruluğunu garanti ederler.
Ayrıca, navigasyon ve haritacılık alanında da teorem büyük bir rol oynar. GPS cihazları, üçgenleme adı verilen ve Pisagor Teoremi’ne dayanan bir süreç kullanarak kesin konumlar belirler. Sistem, uydu sinyallerinden gelen mesafeleri hesaplar ve teoremi kullanarak hassas coğrafi koordinatlar oluşturur.
Gökbilimciler de gök cisimleri arasındaki mesafeleri hesaplamak için bu teoremi kullanır. Yıldızların ve gezegenlerin pozisyonlarını belirlerken, teoremle bu cisimler arasındaki mesafeleri tahmin eder ve evrenin devasa ölçeğini anlamamıza katkı sağlarlar.
Sonuç olarak
Pisagor Teoremi sadece ders kitaplarına hapsolmuş bir matematiksel kavram değildir. Tarihi, antik uygarlıkların zekasını yansıtırken, uygulamaları onun zamansız önemini gösterir. Binalar inşa etmekten evreni keşfetmeye kadar, bu basit ama derin ilişki, dünyayı anlama çabamızda vazgeçilmez bir araç olmaya devam etmektedir.
Kaynaklar ve ileri okumalar için:
- Britannica, The Editors of Encyclopaedia. “Pythagorean theorem”. Encyclopedia Britannica, 10 May. 2024, https://www.britannica.com/science/Pythagorean-theorem. Accessed 22 May 2024.
- The Pythagorean Theorem Makes Construction and GPS Possible; https://science.howstuffworks.com/
- High school students who came up with ‘impossible’ proof of. Pythagorean theorem discover 9 more solutions to the problem. Yayınlanma tarihi: 28 Ekim 2024. Kaynak site: Live Science. Bağlantı: High school students who came up with ‘impossible’ proof of. Pythagorean theorem discover 9 more solutions to the problem
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel





