Matematik, doğası gereği evrensel ve değişmezdir. Ancak tarih boyunca, bazı kişiler ve kurumlar bilimsel gerçekleri kendi bakış açılarına göre şekillendirmeye çalışmıştır. Bu tür girişimlerin en ilginç örneklerinden biri, 1897 yılında Indiana eyaletinde yaşanan “pi yasası” olayıdır. Eğer doğru zamanda doğru yerde bulunan bir matematikçi bu hataya müdahale etmeseydi, Indiana pi sayısını neredeyse 3,2 olarak kabul edecekti.

Yanlış kanıt girişimleri, matematiksel ilerlemenin doğal engellerinden biri olarak kabul edilmektedir. Genellikle geçerliliği olmayan iddialar temel testlerden geçemediği için unutulmaya yüz tutar. Ancak içlerinden biri sessizce kaybolmadı. Hatta yanlış bir pi (π) değerinin yasalaşma noktasına gelmesine neden oldu.
Pi Yasası Nedir?
“Çemberin karelenmesi” olarak bilinen antik bir problem, matematikçileri 2.000 yıldan fazla bir süre boyunca zorlamıştır. Bu süre içinde hem profesyonel hem de amatör matematikçiler, farkında olmadan binlerce yanlış kanıt yayımlamıştır.

Temel soru şudur. Bir çember verildiğinde, yalnızca pergel ve cetvel kullanarak aynı alana sahip bir kare inşa etnek mümkün müdür? Görünüşte basit olan bu görev, beklenmedik şekilde zor bir problem olmuştur. 1894 yılında doktor ve matematiğe meraklı Edward J. Goodwin ise, bu sorunu çözdüğünü düşünmüştür.
Çözümünden o kadar emin olmuştur ki, 1897’de Indiana eyaletinde buluşunu yasalaştırmak için bir yasa tasarısı hazırlamıştır. Karşılığında, Indiana eyaletinin kanıtını telif ücreti ödemeden kullanmasına izin vereceğini ilan etmiştir ve bu noktada da üç büyük hata yapmıştır.
- 1- Matematiksel araştırmalarda telif hakkı kavramı yoktur.
- 2- Teoremleri yasalarla onaylamak gibi bir gelenek yoktur.
- 3-Goodwin’in iddiası tamamen yanlıştır. Çünkü, çemberin çevresinin çapına oranı olan pi’yi yanlış hesaplamıi ve pi sayısını 3.14159 yerine 3.2 olarak almıştır. Ancak, Indiana Temsilciler Meclisi büyük bir hata yaparak yasa tasarısını oybirliğiyle kabul etmiştir.
Goodwin ayrıca, çalışmasını American Mathematical Monthly dergisinde yayımlamayı başarmıştı. Bu dergi günümüzde oldukça saygın bir akademik yayın olsa da, o dönemde “yazarın talebi üzerine” ibaresiyle gelen tüm makaleleri eleştirel inceleme olmadan yayımlıyordu.
Büyük ihtimalle, tasarıyı değerlendiren politikacılar, makalenin prestijli bir dergide yayımlanmasını Goodwin’in iddiasına güven duymak için yeterli bir sebep olarak gördü.
Çemberi Karelemek ile İlgili Sorun Neydi?
Goodwin’in çabasının imkânsız olduğu aslında başından belli idi. Matematikçi Ferdinand von Lindemann, 1882’de bu görevin yapılamayacağını ispatlamıştı. Bunu anlamak için, yarıçapı 1 birim olan bir çember düşünelim. Alan formülü olan A = πr² kullanıldığında, bu çemberin alanı π olur. Aynı alana sahip bir kare yapmak için, karenin kenar uzunluğunun √π olması gerekir.
Yani, antik çağların büyük geometrik bilmecesi şu basit soruya indirgenir. Elimizde yalnızca pergel ve cetvel varken, tam olarak √π uzunluğunda bir doğru çizebilir miyiz? Eğer bunu başarabilirsek, kalan kenarları dik açılarla tamamlamak oldukça kolaydır.
O zamana kadar matematikçiler, yalnızca belirli uzunlukların pergel ve cetvelle çizilebileceğini fark etmişti. İlginçtir ki, bir uzunluk ancak tam sayılar ve toplama, çıkarma, çarpma, bölme ve karekök alma gibi cebirsel işlemlerle ifade edilebiliyorsa çizilebilirdi. Bu, basit Yunan araçlarıyla bazı karmaşık sayıların bile oluşturulabileceği anlamına geliyordu.
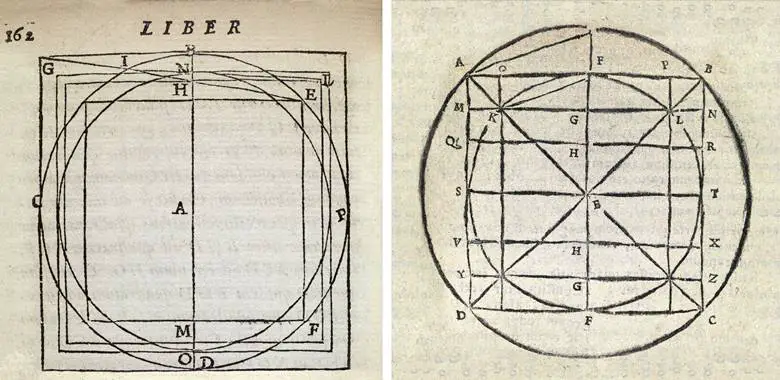
Ancak, bu basit araçlar bazı daha karmaşık olmayan sayıları bile oluşturamaz. Örneğin, 2’nin küp kökü gibi bir sayı, üç kez kendisiyle çarpıldığında 2’yi veren değerdir. Fakat bu sayı, yalnızca toplama, çıkarma, çarpma, bölme ve karekök alma gibi beş temel işlemle ifade edilemediği için pergel ve cetvelle çizilemez.
Lindemann, pi’nin aşkın (transendental) bir sayı olduğunu kanıtladı. Bunun anlamı, toplama, çıkarma, çarpma, bölme ve karekök işlemleriyle pi’yi ifade etmenin imkânsız olmasıdır. Dahası, küp kökler, beşinci kökler gibi daha karmaşık işlemler bile bu durumu değiştirmez.
Lindemann bu sonuca, matematikçi Charles Hermite’in daha önce yaptığı bir çalışmayı genişleterek ulaştı. Hermite, ünlü sabitlerden biri olan e sayısının (Euler sayısı, yaklaşık 2.71828) da aşkın bir sayı olduğunu göstermişti.
Pi, geometrinin en temel şekillerinden biri olan çemberle iç içe geçmiş olmasına rağmen, cebirin en temel diliyle ifade edilemez. Bu nedenle, çemberin karelenmesi problemi matematiksel olarak imkânsızdır. Bu keşif, zamanla günlük dile bile yansıdı. Günümüzde “çemberi karelemek” ifadesi, imkânsız bir görevi başarmaya çalışmak anlamında kullanılan bir deyim haline gelmiştir.
Pi Sayısı 3,2 Olusa Ne Olur?
Bu bilgiler, Goodwin’in neden imkânsızı başarmış gibi göründüğünü de açıklıyor. Pi sayısını 3,2 olarak kabul ettiğinde, aslında problemi kökünden değiştirmiş oldu. Sonucunda 3,2 kesrin 16/5 şeklinde yazılabilir, yani yalnızca tam sayılar ve bölme işlemi kullanılarak ifade edilebilir. Böylece, Pi yerine, rasyonel bir sayı kullanarak problemin zorluğu atlatılır.
Elbette, 1897 yılında Indiana eyalet hükümetinde bu matematiksel detayları bilen kimse yoktu. Yasa tasarısı, meclisten hiçbir muhalif oy almadan geçmişti ve eyalet senatosunun onayına sunulmaya hazırlanıyordu. Eğer kabul edilseydi, Indiana matematik kurallarını yasalarla yeniden yazmaya çalışan bir eyalet olarak tarihe geçecekti.
Ancak tamamen tesadüf eseri, Purdue Üniversitesi’nin matematik bölümü başkanı Clarence A. Waldo, tam da bu sırada eyalet meclisini ziyaret ediyordu. Asıl amacı, üniversitesinin bütçesi için lobi yapmak olan Waldo, bir grup yasa koyucunun matematik üzerine tartıştığını duyunca şaşkınlık içinde konuşmalara kulak verdi. Konunun içeriğini öğrendiğinde, Indiana’nın matematik temellerini sarsacak bir hata yapmak üzere olduğunu fark etti. Sonucunda bu durumu engellemeye karar verdi.

Waldo, mecliste kaldı ve eyalet senatörlerine geometri dersi vermeye başladı. Yasa tasarısının ciddiyetsiz bir girişim olduğunu göstermek için yoğun bir çaba harcadı. Oylama günü geldiğinde, senatörler Waldo’nun dersleriyle donanmış haldeydiler. Ayrıca büyük olasılıkla artan medya ilgisinin de baskısını da hissediyorlardı. Basın, bu durumu alaycı bir dille haber yapmaya başlamıştı. Bu da yasa tasarısının ciddiyetini sorgulayanların sayısını artırmıştı
Sonuç olarak
Indiana Senatosu, yasa tasarısını doğrudan reddetmedi. Ancak, süresiz olarak ertelenmesine karar verdi. Böylece, matematik dünyası büyük bir hata yapmaktan kurtuldu. Chicago Tribune gazetesi, bu olayı sert bir alaycılıkla ele aldı. Yayınladığı başyazıda durumu hicvederek şöyle yazdı:
“Bu değişikliğin anında etkisi, Indiana sınırlarına giren tüm çemberlerin ya daha büyük çevrelere ya da daha küçük çaplara sahip olması olacaktır. Illinois’den veya Ohio’dan gelen bir çember, Indiana toprağına adım attığında oranlarının değiştiğini fark edecektir… 3.2 kadar basit bir pi, her türlü karmaşıklıktan arınmış olmalı, ancak yine de inatçı davranırsa, hiç şüphe yok ki yasama meclisi bir ondalık basamağı daha keserek onu 3 olarak ilan edecektir.”
Kaynaklar ve ileri okumalar
That Time Indiana Almost Made Pi Equal to 3.2 And Other True Stories About Pi. Yayınlanma tarihi: 14 Mart 2013. Kaynak site: Smithsionmag. Bağlantı: That Time Indiana Almost Made Pi Equal to 3.2 And Other True Stories About Pi
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel