72 Kuralı, parayla ilgili birçok sohbetin vazgeçilmez konularından biri olmuştur. Yatırımınızı iki katına çıkarmanın ne kadar süreceğini belirleyen bu basit ve neredeyse sihirli hesaplama, finans dünyasının temel araçlarından biridir.

72 Kuralı, ileri matematikle boğuşmadan, önemli finansal veya pratik konular hakkında hızlı zihinsel hesaplamalar yapmanıza olanak tanır. Bu kural, karmaşık finansal analiz araçlarına ihtiyaç duymadan yatırımınızı, borç maliyetinizi veya enflasyonun etkisini anlamanız için pratik bir yol sunar.
Elbette, bu kural mükemmel değildir. Büyüme oranları çok düşük veya çok yüksek olduğunda, tahminlerin doğruluğu azalabilir. Ancak, tasarruf hesapları, yatırımlar veya enflasyon gibi tipik finansal senaryolar için şaşırtıcı derecede güvenilir bir rehberdir.
72 Kuralı Nedir?
72 Kuralı, paranızın iki katına çıkması için gereken süreyi tahmin etmek amacıyla kullanılan son derece basit bir formüldür. Formül 72 ÷ Yıllık Faiz Oranı = Yıllar biçimdedir. Eğer yatırımınızın yıllık faiz oranı %6 ise, 72’yi 6’ya bölün. Sonuç: 12 yıl. olacaktır. Bu, yatırımınızın iki katına çıkması için gereken süredir.

72 Kuralı Ne işe Yarar?
72 Kuralı, yalnızca paranızın ne kadar sürede iki katına çıkacağını değil, aynı zamanda borçlarınızın büyüme hızını ve yatırım getirilerinizin performansını hızlıca hesaplamanıza yardımcı olur. Eğer üniversite harçları yılda %5 oranında artıyorsa, öğrenim masraflarınızın iki katına çıkma süresi 72 ÷ 5 = 14,4 yıl biçiminde olacaktır.
72 kuralı, geçmiş yatırımlarınızın yıllık getirisini hesaplamak için de kullanılabilir. Örneğin bundan 3 yıl önce 50.000 TL ödeyerek aldığınız bir ev, bugün 100.000 TL olmuşsa 72 ÷ 3 = 24. Bu, evinizin yıllık ortalama %24 değer kazandığını gösterir.
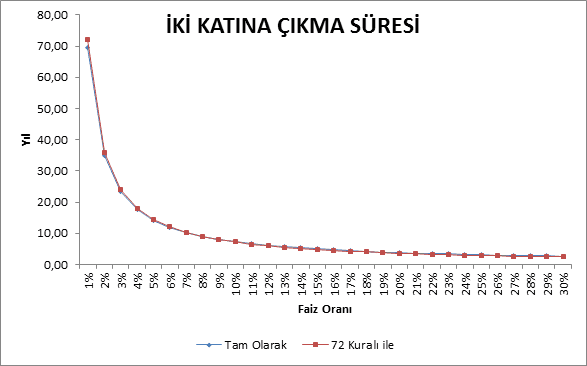
72 Kuralı, iki tasarruf hesabı arasında karar verirken bile hızlı ve etkili bir rehber olabilir. Örneğin, biri %2 yıllık getiri sunarken diğeri %4 yıllık getiri sunuyorsa, kuralı kullanarak paranızın ikiye katlanma süresini kolayca hesaplayabilirsiniz.
- İlk hesap: 72 ÷ 2 = 36 yıl. Yani %2 getiri sunan hesap, paranızı ikiye katlamak için 36 yıl gerektirir.
- İkinci hesap: 72 ÷ 4 = 18 yıl. Bu durumda %4 getiri sunan hesap, paranızı ikiye katlamak için sadece 18 yıl alır.
72 Kuralı, daha yüksek getirileri değerlendirdiğinizde daha etkileyici hale gelir. Örneğin, yıllık ortalama %8 getiri sağlayan bir borsa endeksi fonu, paranızı yalnızca 9 yılda ikiye katlar. (72 ÷ 8 = 9 yıl.) Bu hesaplama, bileşik faizin gücünü soyut bir kavram olmaktan çıkararak elle tutulur hale getirir. Getiriler büyüdükçe, paranızın zaman içinde katlanarak nasıl artacağını görmenin ne kadar basit ve etkili olduğunu bu kural aracılığıyla hızlıca anlayabilirsiniz.
Peki Neden 72 Sayısı?
Bazı meraklı okurlarımızın aklına elbette şu soru gelebilir: Neden 72? İşte bu sorunun arkasında basit bir matematiksel denklem çözümü bulunmaktadır. Bileşik faiz formülü P( 1+ R)N biçimindedir. Şimdi bu formülde anaparamızı 1 ( P=1) ve ulaşmak istediğimiz parayı da 2 olarak alalım. Faiz oranına R, aradan geçen zamana da N diyelim.

Bu durumda denklemimiz 1. (1+R)N = 2 biçiminde olacaktır. Bu durumda (1+R)N = 2 denklemini çözmemiz gerekecektir. İki tarafında logaritmasını alarak işe başlayalım. Logaritma kurallarını uygularsak N. ln( 1+R)= ln2 bulduk. Burada, ln(2) ≈ 0.693 kadardır. Ancak küçük bir basitleştirme yaparak ln(1 + R) ≈ R kabul edeceğiz. Bu varsayım, faiz oranları küçük olduğunda genellikle kabul edilebilir ve pratik hesaplama için yeterince doğrudur.
Bu durumda denklem N × R = 0.693 haline geldi. Ancak 0.693 ile işlem yapmak pratik olmadığından, sonucu daha kullanıcı dostu hale getirmek için 0.693’ü 100 ile çarparak 69.3 elde ederiz. Burada 69.3, aslında kuralın temel sayısıdır. Ancak 69.3 ile işlem yapmak pratik değildir.
Sonraki sayı olan 70’i kullansak bu seferde sadece 7 , 5 ve 2 için kolay işlem yapabileceğiz. Oysaki 72 sayısının bölen sayısı çok daha fazladır. ( 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36 ve 72). Bu nedenle, pratik hesaplamalar için en uygun sayı olarak 72 tercih edilmiştir.
Sonuç olarak
72 Kuralı, üstel büyümenin matematiksel temellerine dayanan basit ama etkili bir araçtır. Mükemmel değildir; özellikle çok yüksek veya çok düşük faiz oranları söz konusu olduğunda doğruluğu azalır. Ancak %4 ile %15 arasındaki faiz oranları için oldukça güvenilir sonuçlar verir. Faiz oranlarına bağlı olarak, 72 Kuralı yerine kullanılan farklı yaklaşımlar da bulunmaktadır:
- 70 Kuralı: %2 ile %5 arasındaki daha düşük getiri oranları için 70 Kuralı daha doğru sonuçlar verir. Bu, 72 Kuralı ile aynı formüle dayanır, ancak faiz oranına 70’i bölerek hesaplanır.
- 74 Kuralı: %10-%12’nin üzerindeki getiriler için 74 Kuralı daha uygundur. Bu, yüksek faiz oranlarında bileşik büyümeyi daha doğru bir şekilde tahmin eder.
Ekonomistler, 72 Kuralı’nın kökenini, finansal hesap makineleri bulunmadan çok önce bileşik faizin gücünü keşfeden 15. yüzyıl tüccarlarına dayandırır. Bu tüccarlar, yatırımların ve borçların büyüme hızını tahmin etmek için bu basit ama etkili yöntemi geliştirmişlerdir. Günümüzde, bu kural, finansal planlama ve kişisel yatırımlar için temel bir araç olmaya devam etmektedir.
Kaynaklar ve ileri okumalar için:
- Forget perfect pizzas, here are four things simple maths really can help you with. Yayınlanma tarihi: 7 Kasım 2013. Kaynak site: Conversation. Bağlantı: Forget perfect pizzas, here are four things simple maths really can help you with
- Have we caught your interest?; yayınlanma tarihi: 1 Temmuz 2020; Kaynak site: Plus Math. Bağlantı: Have we caught your interest?;/
- The Rule of 72 is a quick and simple formula to. Estimate when your investments will double. Kaynak site: Business İnsider. Yayınlanma tarihi: 21 Ekim 2021. Bağlantı: The Rule of 72 is a quick and simple formula to. Estimate when your investments will double
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel






