Bir uçak bileti satın almanız, satın aldığınız uçuşu planladığınız zamanda yapacağınızı garanti etmez. Bazen check-in aşamasında uçakta yer olmadığı ve bir sonraki uçakla gitmeniz gerektiği söylenebilir. Bu duruma Overbooking adı verilmektedir.

Overbooking, özellikle yolcu trafiğinin yoğun olduğu dönemlerde, rezervasyon iptaline karşı havayolu işletmesinin boş koltuktan zarar etme riskini azaltmak için gerçekleştirdiği fazladan rezervasyon işlemidir. Diğer bir deyişle, havayolu gerçek koltuk kapasitesi olan 200 yolcu yerine 220 bilet satmıştır. Aynı durum kimi kişilerin başına otel rezervasyonları esnasında da ne yazık ki gelmektedir.
Şirketlerin bu davranışının nedeni, tamamen karları maksimize etmek ile alakalıdır. Bunun için de istatistiklere güvenirler. Çünkü biletini alan herkesin uçuşa gelmeyeceğini bilirler.
Overbooking Nedir?
Overbooking, özellikle “yolcu trafiğinin yoğun olduğu dönemlerde, rezervasyon iptaline karşı havayolunun boş koltuktan zarar etme riskini azaltmak için gerçekleştirdiği fazladan rezervasyon işlemine verilen isimdir. Bu nedenle her yıl yaklaşık 50 bin kişi bileti olduğu halde uçağa binememektedir.

Maksimum 200 koltuk kapasitesinden yalnızca 185’inin uçuş için geldiğini varsayarsak, bu durumda 15 koltuk boş kalır. Havayolu, kayıpları önlemek için bu koltukları hızlı bir şekilde satmaya çalışabilir. Ancak bu son dakika da kolay değildir.
Bunun yerine havayolunun yaptığı şey, önceden 220 koltuk satmaktır. Bunun sonucunda da 15 yolcu gelmediği ve 205 yolcu geldiği için, sadece 5 hoşnutsuz yolcuyla ilgilenmeleri gerekecektir. Bu 5 yolcuyu hoşnut etmek için yapacakları harcamalar, uçağın 15 boş koltukla havalanmasına izin vermeleri durumunda yaşayacakları zarardan çok daha azdır.
Örneğin, 220 yolcudan 185’i 200$’lık bir uçak bileti için gelirse, havayolu 220×200= 44000$ kazanır. Çifte rezervasyon yerine 200 bilet satmış olsaydı, yalnızca 200×200=40000$ kazanırdı. Bu da temelde 4000$’lık bir kayıptır. Tek bir yolcu için tam tazminatın 500$ olduğunu varsayarsak, havayolu tarafından 5 kişi için kaybedilen para 5×500=2500$ olur. Bu durumda havayolu 1500$ kardadır.
Havayolları fazladan kaç koltuk satacaklarına nasıl karar verir?
Havayolları istatistikler ile düşündüğümüzden çok daha fazla ilgilenmektedir. Geçmiş verilerden yola çıkarak bilet alan her kişinin yola çıkmayacağını bilirler. Aslında her biletli müşterinin uçuşa zamanında gelme olasılığı % 90’dır.
Bilet satın alan her kişinin karşısında aslında iki olasılık vardır. Bu iki olasılık herkes için eşit ve birbirinden bağımsızdır. Bir kişinin uçağına binme olasılığını p ve binmeme olasılığını da 1- p olarak kabul edelim. Uçağımızın koltuklarının sayısı C kadar ve havayolu şirketinin sattığı uçak bileti de y kadar olsun. Ancak satılan bilet sayısı mevcut koltuk sayısından daha fazla olmalı. Havayolunun vermesi gereken karar bu fazlalığın ne kadar olacağıdır.
Olasılık dağılımları, önceden emin olamayacağınız birden fazla sonucu olan süreçleri tanımlamamıza yarar. Bir olayın başarılı ya da başarısız olabileceği tekrarlanan deneylerle hesaplamaya çalışan bir olasılık dağılımı vardır. Binom dağılımı adı verilen bu dağılım, belirli sayıda denemede belirli sayıda başarılı sonucun gözlemlenme olasılığını belirler.
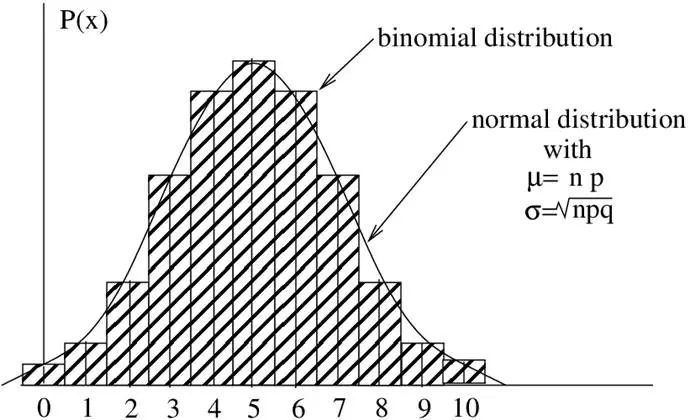
Yukarıdaki grafik, bir bozuk paranın on kez atılmasının binom dağılımını göstermektedir. En sağdaki küçük çubuk, on atışın her seferinde tura geldiği durumu gösterirken, en soldaki çubuk kaç kez hiç tura atmadığınızı gösterir. Ortadaki uzun çubuk ise ne sıklıkla on atışın beşinde tura attığınızı gösterir. Bu çubuk, en olası sonuç olduğu için en yüksek olanıdır.
Overbooking Nasıl Hesaplanır?
Şimdi yukardaki bozuk para örneğini uçaklara uygulayalım. Burada her yolcu deneyin bir denemesi olarak kabul edilir. Bilet aldıkları bir uçağa zamanında gelmeleri başarıdır, gelmemeleri de başarısızlıktır. Bu durumda binom dağılımını kullanarak y bileti sattığımız uçuş için z kişinin gelme olasılığını yazabiliriz. Burada z 0 ile y arasında bir sayı olmalıdır.

Bu örnekte yolcuların sadece küçük bir yüzdesini geri çevirmek ve overbooking nedeniyle satılacak fazladan bileti en az seviyeye indirmek istiyoruz. Uçuşta birinin geri çevrilmesi için, ortaya çıkan sayı Z (y), koltuk sayısı C’den büyük olmalıdır. Şimdi bu bilgiyi yukarıdaki denklem ile birleştirelim. Aşağıdaki ifade, iki bağımsız olaydan herhangi birinin meydana gelme olasılığının, tek tek olayların olasılıklarının toplamına eşit olmasından kaynaklanmaktadır.

Bunu bir örnekle açıklayalım. % 5’lik bir iptal oranı olsun (yani p = 0,05 ). C = 100 yolcu kapasiteli bir uçak için, sayının kapasiteyi aşma olasılığını % 5’in altında tutmalıyız. Bu durumda Y = 101 için P [Z (101)> 100] =% 0,56, y = 102 için P [Z (102)> 100] = % 3,40 ve y = 103 için P [ Z (103)> 100] =% 10.65 olacaktır. Yani havayolu firması zarar etmemek için 102 bilet satmalıdır. Aşağıdaki tablo binom dağılımı tarafından verilen ilgili olasılıkları göstermektedir.
| Satılan Koltuk Sayısı | Olasılık |
| 101 | %0.56 |
| 102 | %3.4 |
| 103 | %10.65 |
| 104 | %23.08 |
| 105 | %39.24 |
| 106 | %56.22 |
| 107 | %71.21 |
| 108 | %82.67 |
| 109 | %90.40 |
| 110 | %95.08 |
Yukarıdaki hesaplamalar konu hakkında bir ön fikir edinmeniz içindi. Daha gelişmiş yöntemler, bir yolcuyu geri çevirmenin maliyetini de hesaba katar. Sonucunda tazminat maliyetleri çok yüksekse, havayolunun overbooking yapmanın bir faydası olmayacaktır. Bu sadece itibarını zedeleyecektir.
Kaynaklar ve İleri Okumalar:
- Overbooking: How to avoid plane rage; yayınlanma tarihi: 13 Temmuz 2017; Bağlantı: https://plus.maths.org
- Kim, Seongmoon & Giachetti, Ronald. (2006). A Stochastic Mathematical Appointment Overbooking Model for Healthcare Providers to Improve Profits. Systems, Man and Cybernetics, Part A: Systems and Humans, IEEE Transactions on. 36. 1211 – 1219. 10.1109/TSMCA.2006.878970.
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel





