Örümcekler neredeyse 400 milyon yıldır dünyada yaşıyor. Okyanustan çıkıp karada yaşamaya başlayan ilk hayvanlar arasındaydılar ve tüm kitlesel yok oluşlardan kolaylıkla kurtuldular. Fosiller bizlere, 30 milyon yıl önceki örümceklerin bugünkülerle hemen hemen aynı olduklarını gösteriyor.

Yaklaşık olarak 40.000 türü olan bu canlılar milyonlarca yıldır avlanmak, yumurtalarını bırakmak, dış tehlikelere karşı korunmak için ağ üretiyorlar. Aslına bakarsanız örümcekler, harika bir ağ çeşitliliği oluşturmak için evrimleşmişlerdir. Düşen avı yakalayan yatay tabaka ağlar ve uçan avı yakalayan dikey kafes ağları vardır. Bazı örümcek ağları da üç boyutlu heykellere benzer.
Avustralya’nın kızıl sırtlı örümceği, boncuklu bir perde gibi dümdüz yere kadar uzanan yapışkan bir ağ örer. Bunlar sadece bir kaç örnek. Yani aslında bir değil bir çok ağ modeli doğada karşımıza çıkar.
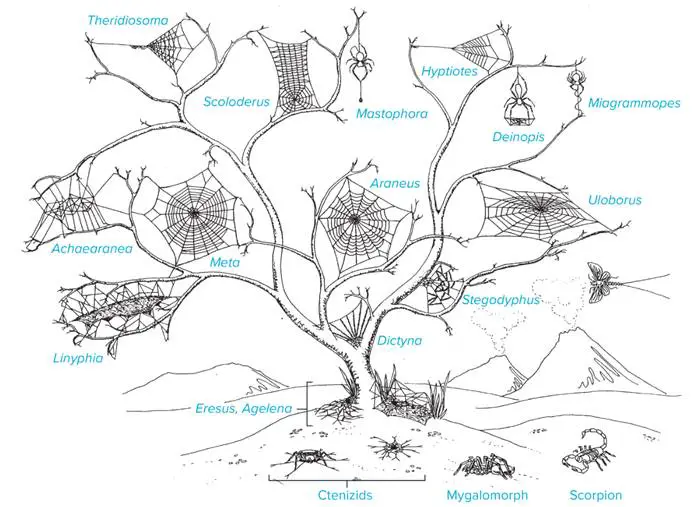
Örümcek ağları mimari ve geometrik şaheserlerdir. Amaçlarını gerçekleştirmek için esnek ve sağlam olmaları ancak aynı zamanda da yeterince yapışkan olmaları gerekmektedir. Tüm bunları aynı anda yapmak için bir örümcek, her biri farklı niteliklere ve işlevlere sahip 7 farklı bezden 7 farklı türde ipek üretir. Üstelik bunu matematiksel ilkelere son derece uygun biçimde yapar.

Bir Örümcek Ağını Nasıl Yapar?
Örümceğin sekiz gözü olmasına rağmen, ağını neredeyse tamamen dokunarak oluşturur. Karnının altında, ağ yapmak için ipeği üretmek ve işlemek için kullandığı, memecik adı verilen altı parmak benzeri uzantı vardır. Her bir memeciğin, sıvı halde farklı türlerde ipek üreten birkaç küçük çıkışı vardır.
Ağın bazı bölümlerinde örümcek tek bir ipek ipliği kullanır. Bununla birlikte, ana yapısal şeritler için, ipe çok benzeyen çok filamentli teller üretir. İpek, havayla temas eder etmez katılaşır. Bunun sonrasında da aynı boyuttaki bir çelik elyaftan yaklaşık beş kat daha güçlü olan ve kopmadan orijinal uzunluğunun yüzde 30’una kadar gerilebilen bir iplik oluşturur.
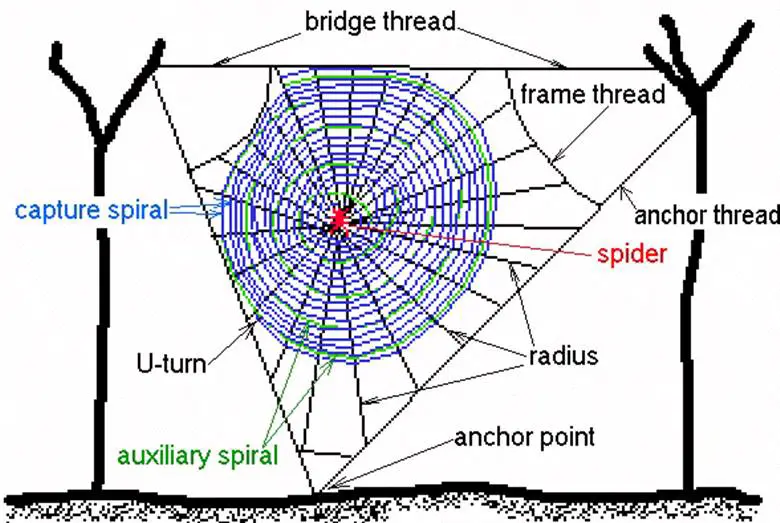
Bir örümcek ağını inşa etmek için önce yapının aralarına gerileceği iki dikey destek bulmalıdır. Bunları dikkatli bir şekilde seçmesi gerekir. Çünkü inşaat sürecinin ilk kısmı için biraz doğadan yardım almalıdır. Örneğin pek çoğumuz iki ucu farklı ağaçlarda olan ve yerden yüksekte kurulmuş ağlar görmüşüzdür. Örümcekler böyle ağlar kurmayı rüzgârın yardımıyla başarır.
Örümcek önce, iki desteğin birine tırmanacaktır. Ardından ipek ipliğin bir ucunu tutturur ve ipliği aşağıya doğru döndürür. Bu sırada alt uçtan serbestçe asılı kalır. Sonrasında da hafif bir rüzgarın onu diğer desteğe doğru sallamasını bekler. Bu rüzgar gelir gelmez, örümcek ikinci desteğe tutunur ve ilk ipliğin serbest ucunu yapıştırır.
İpek o kadar ince ve hafiftir ki, bu adımı gerçekleştirmek için en yumuşak hava hareketinden daha fazlasını gerektirmez. Bu yolla birkaç gidiş gelişte ağın Y biçiminde bir iskeleti meydana gelir. Bundan sonra iskeletin merkezi çevresinde halkalar yaparak ağı tamamlar. En sonunda da ağın merkezine geçerek yemeğini bekler. Yaptıkları şekiller birer geometri ustası olduklarını kanıtlar niteliktedir.
Örümcek Ağının Geometrik Özellikleri
Ağın genel şekli, örümceğin bazı çok basit adımları gerçekleştirmesinin sonucudur. Bir örümceğin ağını inşa etmesi bir ila üç saat sürer, genellikle geceleri yaptığı bir görevdir. Örümcekler, ağ örerken mesafeleri ölçmek için kendi vücutlarını kullanır. Örneğin spiraller arasındaki mesafe arka ayaklarının ucuyla düzeleri arasındaki mesafeyle orantılıdır.
Sarmal eğrilerden meydana gelen ağlar, görünmezlik ve geniş yakalama alanının eşsiz bir kombinasyondur. Ağı oluşturan eğriler merkezden çevreye doğru sürekli büyümelerine rağmen, ağın genel görünümünde hiçbir değişiklik meydana gelmez.
Ağ örme sürecinin bir aşamasında örümcek, ağın yeterli yoğunluğa sahip olması için, ardışık dönüşler arasındaki mesafeyi eşit tutmaya çalışır. Bunun sonucunda da aşağıda da gördüğünüz ve matematikçilerin aritmetik spiral dediği bir yapıyı üretir.
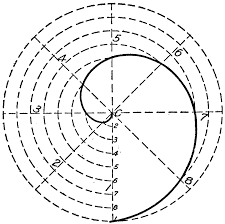
Ağ örülürken önce merkezden dışa doğru (radyal yöndeki) iplikler gerilir. Örümcek ağın merkezini yaklaşık beş adet dairesel iplikle güçlendirdikten sonra içten dışa doğru geniş aralıklı bir spiral yapar. Yapışkan özelliği olmayan bu spiral örümceğin ağı örerken rahatlıkla hareket edebilmesi içindir. Bir sonraki aşamada örümcek bu kez dıştan içe doğru yapışkan spirali yapmaya başlar. Bu spiralin aralıkları daha sıktır ve avları yakalamak içindir.

Yapışkan spiraller yapıldıktan sonra, herhangi bir işe yaramayacağı için yapışkan olmayan spiral kaldırılacaktır. Ağın kurulumu tamamlandıktan sonra da örümcek avını beklemeye başlar.
Örümcekler Matematik Biliyor Olabilir mi?
Sonuç olarak sizin de gördüğünüz gibi örümcekler, inanılmaz planlama becerileri ve titiz ve işlevsel hesaplamaları ve tüm bunları izin verecek biçimde gelişmiş biyolojileri ile gerçekten doğanın en yetenekli mühendislerinin başında gelir.
Ancak elbette bir örümcek ağını inşa ederken matematiksel hesaplama yapması gerekmez. Örümcek mükemmel bir geometrik tasarımdan ziyade, az malzeme ile, sağlam bir yapı inşa elde etmek niyetindedir. Bu da örümceğin içgüdülerine kodlanmış bir beceridir. Doğanın her noktasında matematiğin izine rastlamak mümkündür. Çoğunun da temelinde aynı dürtü yer almaktadır.
Kaynaklar ve ileri okumalar
- How spider silk is one of the most versatile materials on Earth; Yayınlanma tarihi: 12 Eylül 2019; bağlantı: https://www.nationalgeographic.com/
- The Math Instinct: Why You’re a Mathematical Genius (Along with Lobsters, Birds, Cats, and Dogs); Bağlantı: https://www.maa.org/
- Sticky Science: the Evolution of Spider Webs. Yayınlanma tarihi: 31 Ekim 2018; Bağlantı: https://www.scientificamerican.com/
- Ask Smithsonian: How Do Spiders Make Their Webs? Yayınlanma tarihi: 3 Aralık 2015; Bağlantı: https://www.smithsonianmag.com
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel