Ortalamaya gerileme ya da ortalamaya geri dönüş, genellikle zararsız bir olgudur. Ancak bu doğal değişim süreci yanlış yorumlandığında, beklenmeyen sonuçlara veya hatalı kararlar alınmasına neden olacaktır.

Hepimizin hayatında, bulunmaktan büyük keyif aldığımız ve hiç bitmesini istemediğimiz anlar vardır. Mekan, atmosfer, yemekler, sohbet—her şey mükemmeldir. Ancak aynı deneyimi tekrar yaşama çabası genellikle hayal kırıklığına yol açar. Bunun nedeni, o mükemmel anın, tamamen sizin lehinize gelişmiş bir dizi tesadüfi olaydan kaynaklanmasıdır.
Mükemmel bir akşamı tekrar yaşamaya çalıştığınızda, en az bir şeyin kusurlu olması olasılığı oldukça yüksektir. Belki yan masadaki çift fazlasıyla gürültücüdür ya da garson siparişinizi yanlış getirir. Neyse ki tam tersi durumda, yani berbat bir deneyimi tekrarlamak zorunda kalırsanız, ikinci sefer de genellikle o kadar kötü olmayacaktır.
Bu fenomene “ortalama gerileme” veya “ortalamaya geri dönüş” (Regression To The Mean) denir. Terim, ilk kez İngiliz bilim insanı Sir Francis Galton tarafından ortaya atılmıştır. Ortalama gerileme, istatistikte bir olayın ekstrem bir şekilde meydana geldikten sonra, tekrarlandığında daha ortalama bir sonuca yakınlaşma eğilimini ifade eder.
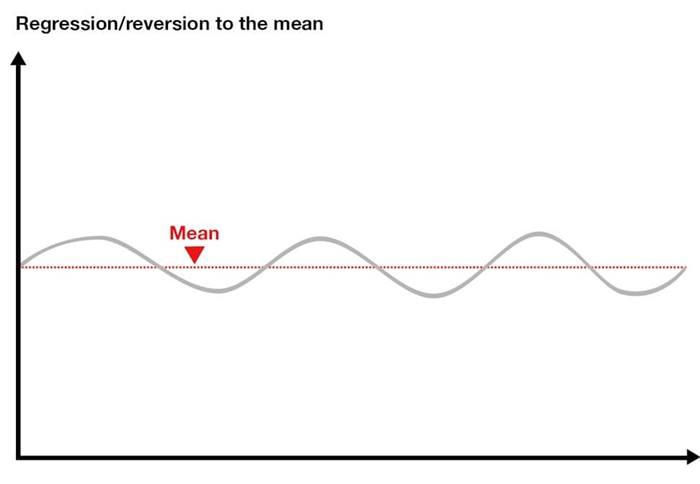
Ortalamaya Geri Dönüş Nedir?
Galton, ebeveynlerden alınan genetik mirasın bireyin kaderini ne ölçüde etkilediğini belirlemeye karar verdi. Bu çalışmalarda ölçmesi kolay bir özellik olduğu için insanların boylarını incelemeye başladı. Galton’un gözlemleri, uzun boylu ebeveynlerin çocuklarının da uzun boylu olma eğiliminde olduğunu ortaya koyuyordu.
Bu durum, herkesin sezgisel olarak bildiği bir gerçek gibi görünüyordu: Genetik faktörler, fiziksel özellikler üzerinde belirgin bir etkiye sahipti. Ancak Galton’un çalışmaları dikkat çekici bir fenomene işaret etti.
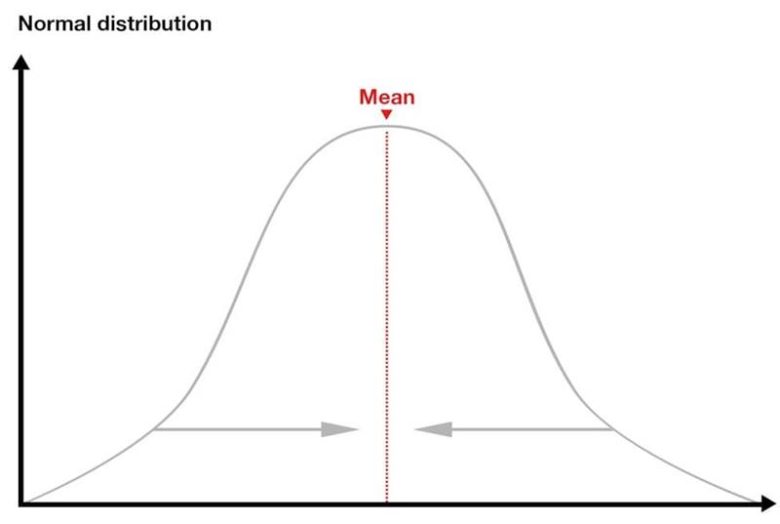
Bu çocuklar, anne babaları kadar uzun olma eğiliminde değillerdi. Aynı durum, kısa boylu anne baba için de tersi yönde geçerliydi; bu ailelerin çocukları kısa olma eğilimindeydiler fakat anne babaları kadar kısa değillerdi.
Galton, bu keşfini 1889 yılında yayımladığı Natural Inheritance (Doğal Kalıtım) adlı kitabında kaleme aldı.

Galton, boyun yalnızca doğuştan gelen özelliklerin değil, aynı zamanda dış faktörlerin de bir kombinasyonu tarafından belirlendiğini anlamıştı. Bu dış faktörler, bireyin içinde bulunduğu çevreyi, çocukluk dönemindeki sağlık koşullarını ve hatta basitçe şansı içerir.
Uzun boylu insanlar uzun boylu olma eğilimindedir çünkü genetik mirasları buna zemin hazırlar. Başka bir deyişle, bu kişiler iyi genlerle doğmuşlardır. Ancak bu yalnızca hikayenin bir kısmıdır; genetik mirasın yanı sıra, çevresel koşullar ve şans gibi faktörlerin de uzun boylu olmalarında etkisi büyüktür.
Ortalamaya Gerileme Neden Gerçekleşir?
Uzun boylu kişilerin çocukları genlerini paylaşacaktır. Ancak bu çocukların boylarını kalıtımın gerektirdiğinden daha fazla uzatmak üzere dış faktörlerin bir kez daha bir araya gelmeleri olası değildir. Bu nedenle bu çocuklar ortalama bir insandan daha uzun boylu olacaklar ancak anne babaları kadar uzamayacaklardır. Bu durum kalıtımla şansın iç içe işleyişinin basit bir sonucudur.
Ortalamaya gerileme, tamamen şans tarafından yönlendirilir ve şansın var olduğu her yerde etkisini gösterir. Zaman içinde rastgele dalgalanmalar içeren hemen hemen her durum, potansiyel olarak bu olguya tabidir.
Peki neden bir yazarın ilk romanı büyük bir çıkış yaparken ikinci romanı genellikle ilki kadar başarılı olmaz? Veya neden bir müzik grubunun ilk albümü büyük bir patlama yaşarken ikinci albümü genellikle daha düşük bir etki bırakır? Bunun nedeni, sanatçının söyleyecek bir şeylerinin tükenmiş olması değildir. Asıl sebep, sanatsal başarının, diğer birçok şey gibi yetenek ve şansın bir karışımı olmasıdır. Dolayısıyla, sanatsal başarı da ortalamaya geri dönüş etkisinden kaçamaz.
Benzer bir durum sporda da görülür. Bir futbolcu bir sezonda olağanüstü bir performans gösterdiği için yüksek meblağlı sözleşmelere imza atabilir. Ancak, bu oyuncular bir sonraki sezonda genellikle daha düşük bir performans sergiler. Bunun birçok nedeni olsa da, nedenlerden biri kesinlikle ortalamaya geri dönüş etkisidir.
Büyük sözleşmeyi getiren performans, şans ve yetenek faktörlerinin birlikte çalışmasının bir sonucudur. Fakat bir sonraki sezonda bu faktörlerin tekrar aynı şekilde bir araya gelmesi düşük bir olasılıktır.
Ortalamaya geri dönüş tamamen matematikseldir. Şansın etkisiyle ekstrem bir sonuç elde edildiğinde, bir sonraki durumda sonuç büyük olasılıkla ortalamaya daha yakın olacaktır. Bu basit fakat güçlü prensip, hayatın hemen her alanında karşımıza çıkar.
Sonuç olarak
Ortalamaya gerileme her yerde karşımıza çıkar. Bu olguyu anlamak ve farkında olmak, olağandışı olaylara aşırı tepki vermekten kaçınmanıza yardımcı olur. Ancak ortalamaya gerilemeyi göz ardı etmek ciddi yanlış sonuçlara yol açar.

Örneğin, bir öğretmenin öğrencilerini değerlendirdiğini düşünelim. En iyi sınav sonuçlarını elde eden öğrenciler övgü alır, en kötü notları alanlar ise eleştirilir. Bir sonraki sınavda sıralamalar büyük ihtimalle değişir; farklı öğrenciler en üst ve en alt sıralarda yer alır. Bu değişim, sonucunsa öğretmen, övgünün zarar verdiğini ve cezanın işe yaradığını düşünebilir. Ancak bu, yanlış bir sonuçtur. Değişim yalnızca ortalamaya geri dönüşün bir sonucudur.
Örneğin, bir hastane işlettiğinizi ve size hastane kaynaklı enfeksiyonların geçen ay ortalamadan beş kat daha yüksek olduğunun söylendiğini hayal edin. Bir meslektaşınız size sebebini bildiklerini ve daha fazla belli bir antibiyotiği kullanılarak sorunun çözülebileceğini söylüyor olsun. Onun fikrini kabul edebilirsiniz. Bunun sonucunda sonraki ay enfeksiyonlarda azalma da gözlenebilir.
Bu durumda zihniniz nedensel bir bağlantı kuracak ve antibiyotiklerin gerekliliğine ikna olacaksınızdır. Oysa ki olağandışı enfeksiyon oranı tesadüfi olaylardan da kaynaklanmış olabilir. Ancak bunu göz ardı etmek pek çok potansiyel sorunu da beraberinde getirecektir. Buna bir çözüm biraz daha fazla veri toplamak ve acele karar vermemektir. Çünkü ortalamaya geri dönüş her yerdedir.
Kaynaklar ve ileri okumalar
- Barnett AG, van der Pols JC, Dobson AJ. Regression to the mean: what it is and how to deal with it. Int J Epidemiol. 2005 Feb;34(1):215-20. doi: 10.1093/ije/dyh299. Epub 2004 Aug 27. Erratum in: Int J Epidemiol. 2015 Oct;44(5):1748. PMID: 15333621.
- Regression to the mean, or why perfection rarely lasts. Yayınlanma tarihi: 26 Mart 2017. Kaynak site: Conversation. Bağlantı: Regression to the mean, or why perfection rarely lasts
- Morton V, Torgerson DJ. Effect of regression to the mean on decision making in health care. BMJ. 2003 May 17;326(7398):1083-4. doi: 10.1136/bmj.326.7398.1083. PMID: 12750214; PMCID: PMC1125994.
Matematiksel