Sekiz boyutlu sayılardan oluşan ve oktonyonlar adı verilen bir sistem fizikçilerin tüm evreni tanımlayan tek bir matematiksel çerçeve bulmalarına yardımcı olacak mı?
Parçacık fiziğinin standart modeli güçlü kuvvet, zayıf kuvvet ve elektromanyetik kuvvetin kuantum kuramlarını bir araya getirir. Her ne kadar çok başarılı bir kuram olsa da standart modelin çeşitli eksiklikleri vardır. Bu nedenle fizikçiler onlarca yıldır standart modeldeki üç etkileşimi tek bir matematiksel çerçevede bir araya getiren bir “büyük birleşik kuram”, hatta kütle çekimi de dâhil tüm fiziksel etkileşimleri açıklayan bir “her şeyin teorisi” geliştirmeye çalışıyor.
Ancak bugüne kadar bu hedefe ulaşılamadı. Bunun üzerine son zamanlarda fizikçiler başka bir soru sormaya başladı. Ya gerçekliği yanlış türde sayılarla tanımlamaya çalışıyorsak? Matematikçiler gerçeklik teorilerimizi oktonyonların diline çevirerek fizikteki en derin problemlerden bazılarını çözebileceklerini düşünüyorlar.
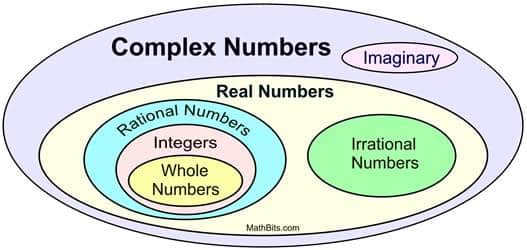
Aslında fizikte bir çıkmaz ile karşılaştığımız zamanlarda arka plandaki matematiği değiştirme fikri ilk değil. Sonucunda Galileo’dan Newton’a, Coulomb’dan Maxwell’e kadar klasik fiziğin tamamı reel sayılara dayanmaktaydı. Ancak ilgili yasalarda, hepimizin aşina olduğu reel sayılar kümesi ile çalışmak mümkün olsa da bir zaman sonra fizikçiler tıkanmıştı. Çünkü negatif bir sayının karekökünü almak reel sayılarda mümkün değildi. Bu tıkanıklık sonucunda karmaşık sayılar ile tanıştık.
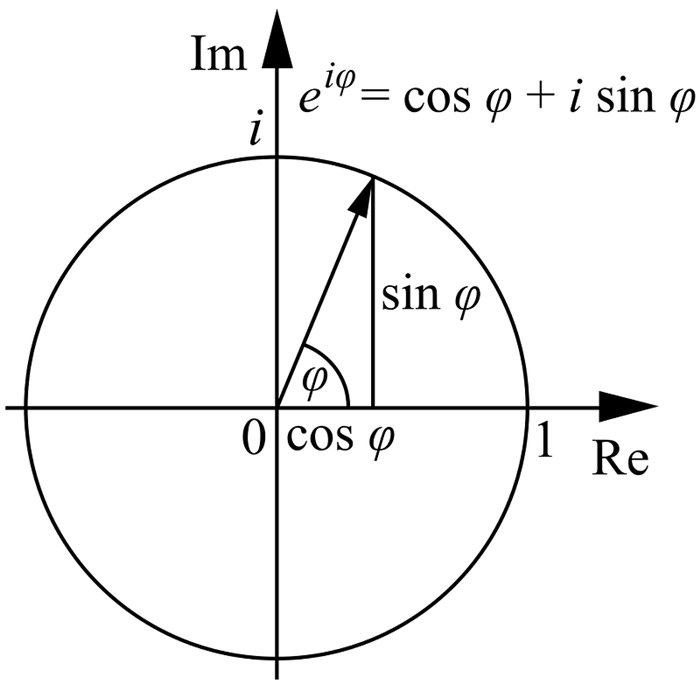
Karmaşık sayılar genel olarak a+ib biçiminde yazılan iki parçadan oluşan sayılardır. Burada a ve b herhangi iki reel sayıyı, i ise i2= -1 eşitliğini sağlayan bir sanal sayıyı gösterir. Karmaşık sayılar üzerinde toplama, çıkarma, çarpma ve bölme gibi işlemleri “düzlem etrafındaki konumları çevirerek ve döndürerek” gerçekleştirebilirsiniz.
Günümüzde parçacık fiziği, elektrik mühendisliği gibi birçok bilimsel alanı karmaşık sayılara güvenir. Ölçülebilir büyüklüğe karşılık gelen gerçek kısmın ve ölçülemeyen gerçekliğe karşılık gelen sanal kısmın birlikteliği, evrenin küçük boyutlardaki davranışını eksiksiz olarak anlamamızı sağlar.
Kuaterniyonlar Nedir?
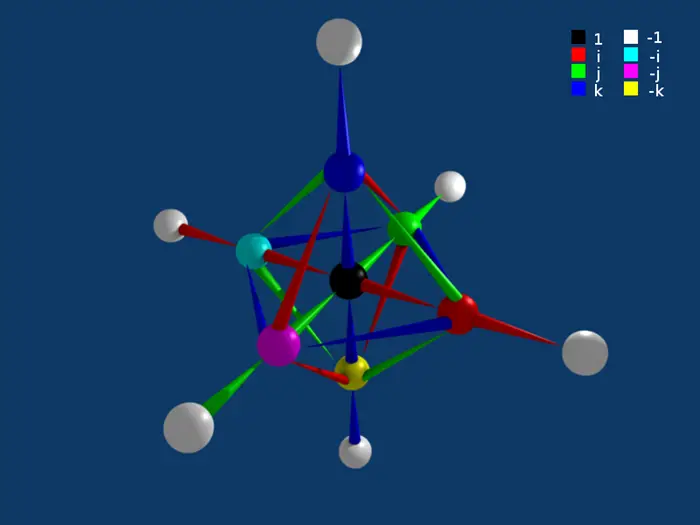
Gerçek, sanal ve diğer iki temel kuaterniyon (j ve k) sayıları arasında nasıl dönüşebileceklerine dikkat edin
Peki ama karmaşık sayılardan daha karmaşık, bir yapı bulmamız mümkün müdür? Elbette bir karmaşık sayının karekökünü aldığınız zaman karşınıza daha karmaşık bir sayı çıkacaktır. Ancak temelinde aradığımız cevap bu değildir. Oysa ki karmaşık sayıları yine de bir biçimde genişletmemiz mümkündür. Bu da bizi kuaterniyonlar ile tanıştırır.
İrlandalı matematikçi William Rowan Hamilton, 1843’te karmaşık sayıları belirli bir şekilde eşleştirirseniz 4 boyutlu kuaterniyonlar oluşturabileceklerini keşfetti Bir kuaterniyon q ile gösterilmek üzere q=a + bi + cj + dk şeklinde yazılabilir. Burada a, b, c ve d gerçek sayılar ve i, j ve k ise sanal sayılardır. Her kuaterniyonun, dört boyutlu uzaydaki bir noktanın koordinatları gibi dört parçası vardır.
Kuaterniyonlar çok sayıda fiziksel uygulamayla ilişkilidir. Karmaşık bir sayı, iki boyutlu bir düzlemdeki noktaları temsil ederken, bir kuaterniyon, üç boyutlu uzaydaki noktaları tanımlar. Işık hızına yaklaştıkça uzunlukların nasıl kısaldığını ve zamanın nasıl genişlediğini açıklayan Lorentz dönüşümleri kuaterniyonları kullanır.
Kuaterniyonlar ile sıradan sayılarda yaptığımız gibi toplama, çıkarma, çarpma ve bölme yapmak mümkündür. Ancak iki kuaterniyon çarpıldığında sıraya göre farklı cevaplar verir. Yani değişme özellikleri yoktur. Peki kuaterniyonları daha da genişletmemiz mümkün müdür? Cevap evet olacaktır.
Daha karmaşık yapıya giden bir sonraki adım, 8 bileşene sahip olan oktonyonlara geçmektir. Kuaterniyonların matematiği bilinen bir takım fiziksel teorilerle ilişkiliyken, oktonyonların matematiği bilinen fiziğin ötesine geçen işlemleri tanımlar.
Oktonyonlar Nedir?
Hamilton, arkadaşı John T. Graves’e yeni sayılarından bahsettiğinde Graves, “Neden dört boyutta duralım ki?” diye merak etmişti. Kısa süre sonra, her biri sekiz bileşene sahip olan ve oktonyon adı verilen bir sayı sistemi buldu
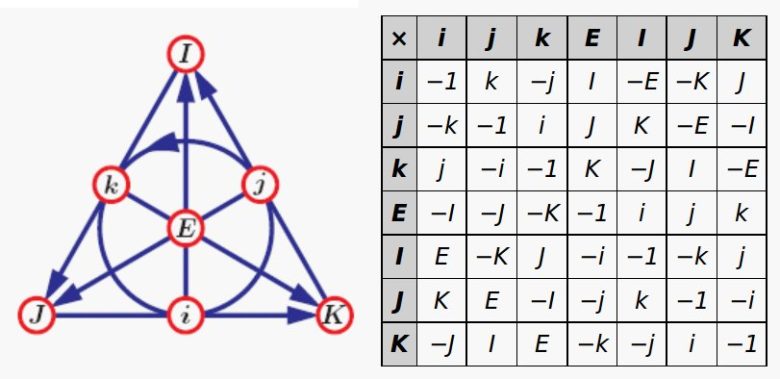
Oktonyonlar sekiz ayrı birim sayının lineer kombinasyonu olarak ifade edilen hiperkompleks sayılardır. Daha basitçe söylememiz gerekirse bunlar sekiz boyutlu uzaydaki noktalardır. Bu sayılar bize farklı boyutlara kapı açar. Ancak bunun karşılığında da bir ödün vermemiz gerekir. Çünkü bu sayılar da hem değişme hem de birleşme özelliğini sağlamaz.
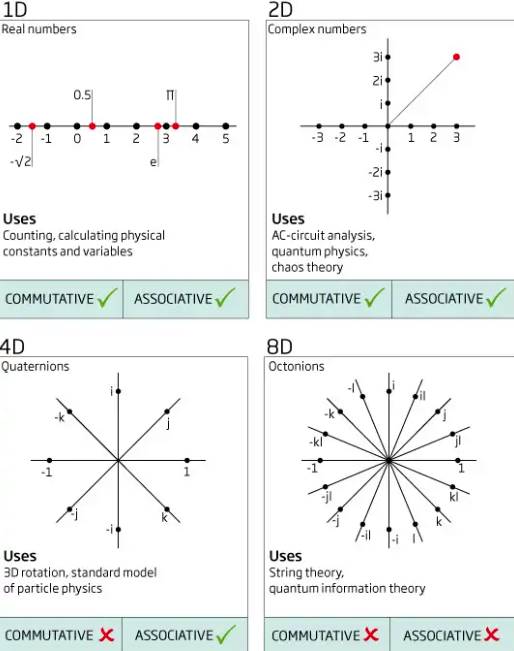
Oktonyonlar Bir İşe Yarayacak mı?
Aslına bakarsanız uzun süre için bu cevap hayır idi. Oktonyonlar bilimsel bir meraktan daha fazlası olarak kabul edilmedi. Ancak bir ker daha, fizikteki gelişmeler matematiği de etkileyecekti. Örneğin Sicim teorisi süpersimetri fikrine dayanır. Her madde parçacığının bir “ikiz” kuvvet parçacığı vardır ve madde ile kuvvet parçacıklarını değiştirirsek fizik yasaları değişmeden kalır. Ancak bu sadece 1, 2, 4 veya 8 boyutta mümkündür.
Ve hatta, biri zaman ve diğeri sicim boyutu için olmak üzere iki bileşen daha ekleyerek 3, 4, 6 ve 10 boyutlu uzaylar da elde ederiz. Şu anda, oktonyonlara dayanan 10 boyutlu uzay, sicim teorisyenleri tarafından evreni tanımlamaya yönelik olası bir aday olarak değerlendiriliyor.
Sonuç olarak oktonyonların kendisi hiçbir zaman gerçekliğin nasıl çalıştığına dair bize bir cevap veremez. . Ancak matematiksel yapıları inanılmaz bir zenginlik barındırmaktadır. Bu zenginliğin Evrenimiz için bir anlam ifade edip etmediğini kimse bilmiyor.
Kaynaklar ve ileri okumalar
- Octonions: The strange maths that could unite the laws of nature. Yayınlanma tarihi: 16 Ağustos 2022. Kaynak site: The NewScientist. Bağlantı: Octonions: The strange maths that could unite the laws of nature
- Ask Ethan: Could Octonions Unlock How Reality Really Works?. Yayınlanma tarihi: 21 Ağustos 2019. Kaynak site. Big Think. Bağlantı: Ask Ethan: Could Octonions Unlock How Reality Really Works?
Matematiksel