Ölçmeye çalıştığınız şey ne olursa olsun eğer örneklem boyutunuz yeterince büyükse, her zaman bir çan eğrisi yani normal dağılım elde edersiniz
Bir bebek doğduğunda doktorlar bebeğin kilo, boy, parmak sayısı gibi bir dizi özelliklerini ölçer. Eğer bebek, bu özellikler bakımından ortalama değerlere sahipse “normal”, yani sağlıklı kabul edilir. Fakat bebek örneğin ortalamadan çok fazla ya da çok az kiloya sahipse “normal değil” olarak nitelendirilir. Peki bu normalleri neye göre seçiyoruz?
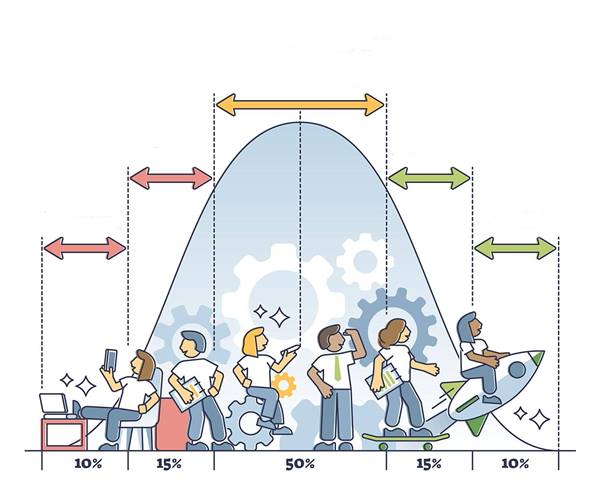
Çoğu zaman normal kilo, normal boy gibi birtakım normal özelliklerden bahsederken sanki bunu keyfi olarak seçmişiz gibi gelir. Fakat olaya matematiksel açıdan baktığımızda somut özellikler bakımından normal kavramı son derece evrenseldir. Bu durumu açıklamak için boy örneğinden yola çıkalım. İnsanların genelini düşündüğümüzde çoğu insan belli bir boy aralığındadır. Çok kısa ya da çok uzun insanlar nadirdir. Bu da çoğunluğun bulunduğu boy aralığının normal olarak adlandırılmasına sebep olur.
Ancak bu durum sadece boy uzunluğunda geçerli değildir. Doğada ve günlük hayatta birçok şey normal dağılım gösterir. Peki neden? Aslında bu nispeten basit bir soru ancak büyük bir matematiksel derinliğe de sahip. O nedenle bu yazımızda normal dağılımı beraber anlamaya çalışalım.
Olasılık Dağılımları Nedir?
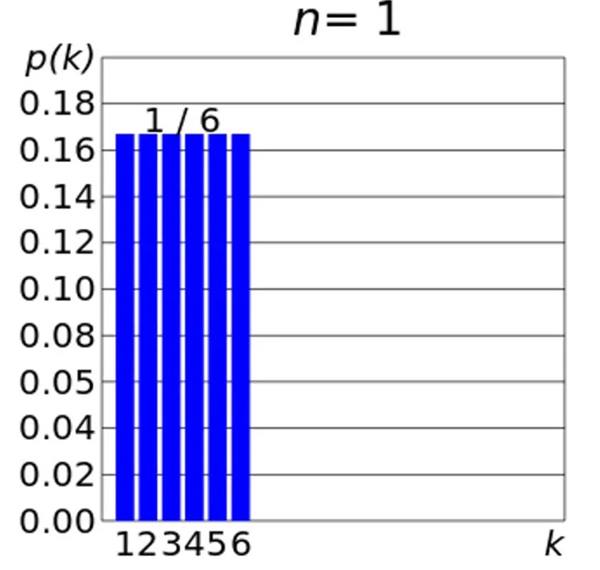
Olasılık dağılımları, önceden emin olamayacağınız birden fazla sonucu olan süreçleri tanımlamamıza yarar. Bir örnek, bir zarın atılmasıdır. Bildiğiniz gibi 6 olası sonuç vardır. Zar adil olduğu sürece, bunların hepsinin gerçekleşme olasılığı eşittir. Bu, zar atışınızla 1, 2, 3, 4, 5 veya 6 alma şansının %16,666 olduğu ve başka hiçbir sonucun mümkün olmadığı anlamına gelir.
Bunu görselleştirseniz normal dağılım olmadığını yani çan eğrisi şeklinin karşımıza çıkmadığını görürsünüz. Gördüğünüz gibi her sonucun eşit olasılığa sahip olduğu olaylarda tek tip bir dağılım söz konusudur.
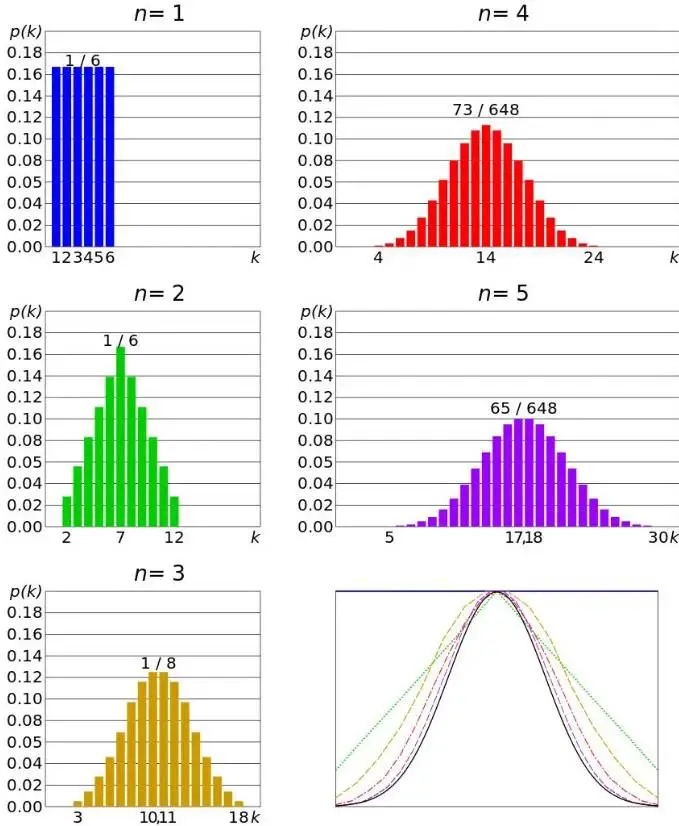
Ancak şimdi bir yerine iki zar atarsanız ne olur? Elbette, her bir zar, daha önce sahip oldukları olasılıkların aynısına sahiptir. Yani her birinin gelme olasılığı %16,666’dır. Bununla birlikte, iki zarı birlikte attığımızda olası sonuçlar kümesinde artık düz bir dağılım görmezsiniz. Aşağıda da gördüğünüz gibi şeklimiz giderek daha fazla çan eğrisine benzemeye başlar.
Zarların gösterdikleri sayıları toplarsanız, 11 olası sonucunuz olur. Ancak hepsinin olasılığı eşit değildir. Birçok farklı kombinasyon size nihai sonucu 7 (1 ve 6, 2 ve 5, vb.) verebileceğinden, 7 ile sonuçlanma olasılığınız 2 ile sonuçlanmaktan çok daha olasıdır.
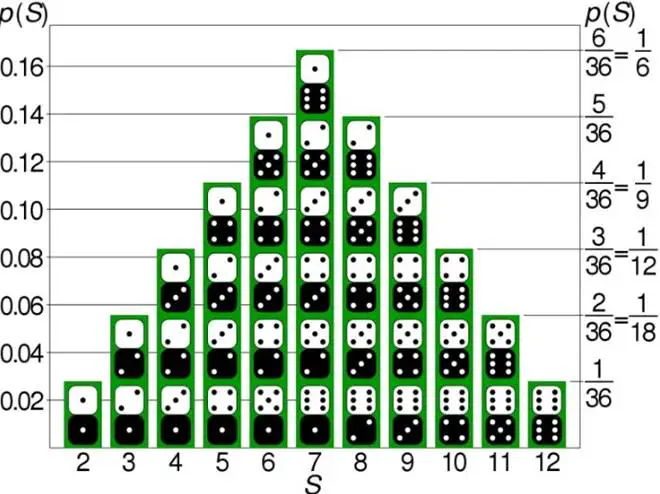
Aslına bakarsanız daha fazla zarı bir arada atarsanız ve olası sonuçları çizerseniz ortaya çıkan şekil giderek daha fazla çan eğrisine benzeyecekti.
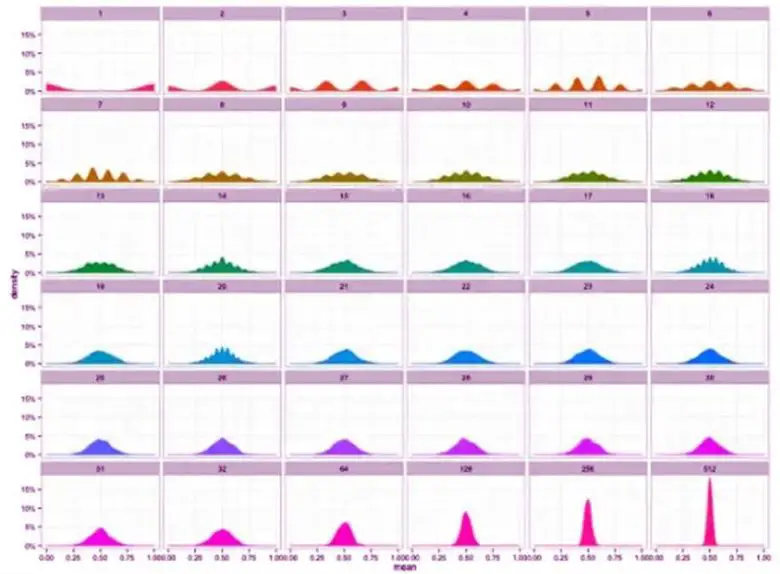
Bu özel durum, mümkün olan yalnızca iki sonucun olduğu ve çoğu zaman bu iki sonucun her birinin eşit derecede olası olduğu durumlarda ortaya çıkar. Bunun bir başka örneği de adil bir para ile yazı tura atmaktır. Giderek daha fazla sayıda bozuk para atarsanız çan eğrisi şekli ile bir kere daha karşılaşırsınız.
Normal Dağılım İle Nasıl Tanıştık?
Bu durum ilk olarak modern olasılık teorisine önemli katkılarda bulunan Abraham de Moivre tarafından gözlemlenmişti. De Moivre’nin 1756 tarihli The Doctrine of Chances (Şansların Doktrini) isimli kitabında bu konuyu açıklamıştı.
Bu durumda n tane deneme yaparsanız ve her denemenin p başarı olasılığına sahip olduğunu biliyorsanız, o zaman sonucunda normal bir dağılım elde edeceksiniz. Ortalama değer np kadar, çan eğrinizin standart sapması da √(np(1-p)) olacaktır. Ne kadar çok deneme kullanırsanız sonuçların dağılımı normal dağılıma o kadar yakın olur.

Bu kavram ilk olarak Moivre tarafından geliştirilmiş olmasına rağmen, 1930’da Macar matematikçi George Pólya’nın onu merkezi limit teoremi olarak adlandırmasına kadar resmi olarak kullanılmamıştır. İstatistiksel tahmin elde etme sanatına kesinlik kazandıran merkezi limit teoremidir ve aynı zamanda normal dağılımın her yerde karşımıza çıkmasının da arkasındaki sebeptir.
İstatistikteki ana fikir, küçük bir örneğe bakarak bütün bir popülasyon hakkında bir şeyler söyleyebilmenizdir. Bu fikir olmasaydı, kamuoyu yoklamaları veya seçim tahminleri olmazdı. Yeni tıbbi ilaçları veya köprülerin güvenliği gibi şeyleri test etmenizin bir yolu da olmazdı. Bütün bunları merkezi limit teoremi sayesinde yapabiliyoruz.
Normal Dağılımın Özellikleri Nelerdir?
Normal dağılım, ortalamanın her iki tarafında da simetrik olan sürekli bir olasılık dağılımıdır; dolayısıyla merkezin sağ tarafı, sol tarafın ayna görüntüsüdür. Eğrinin altındaki alan olasılığı temsil eder ve eğrinin altındaki toplam alanın toplamı birdir. Normal bir dağılımda veriler ortalama etrafında kümelenme eğilimindedir ve bir değer ortalamadan ne kadar uzaksa, ortaya çıkma olasılığı da o kadar az olur.
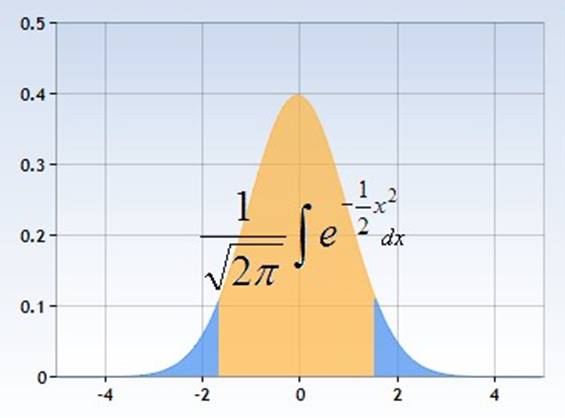
Tamamen normal bir dağılım için ortalama, medyan ve mod aynı değer olur. Ve bu değer eğrinin tepe noktasını oluşturur. Normal dağılıma görüntüsünden dolayı çan eğrisi de denir. Aynı zamanda onu ilk kez tanımlayan Alman matematikçi Carl Gauss’un anısına Gauss dağılımı olarak da bilinir.
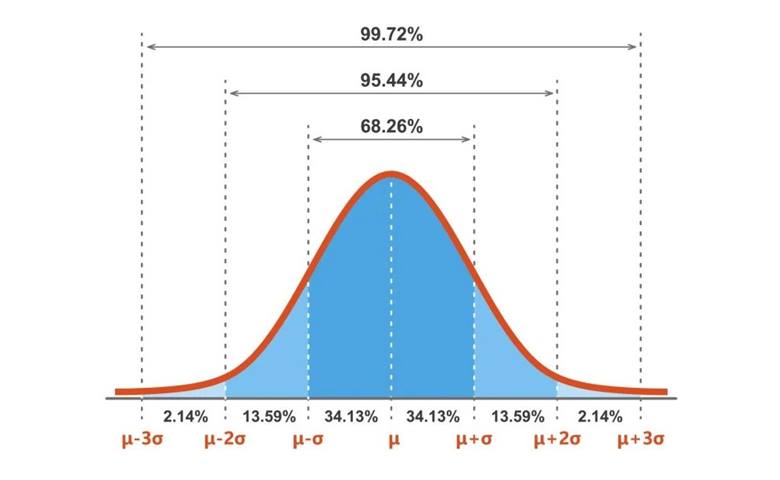
Normal bir dağılım, ortalama ve varyans olmak üzere iki parametreyle belirlenir. Ortalaması 0 ve standart sapması 1 olan normal dağılıma standart normal dağılım denir.
Normal Dağılım Neden Önemlidir?
Normal dağılım ve daha genelinde istatistikteki en önemli olasılık dağılımıdır çünkü doğadaki birçok sürekli veri grafik haline getirildiğinde bu çan şeklindeki eğriyi gösterir. Merkezi limit teoremine göre, verilerin gerçek dağılımına bakılmaksızın, örneklem büyüklüğü arttıkça, bir veri örneğinin ortalaması, söz konusu genel popülasyonun ortalamasına daha yakın olacaktır.
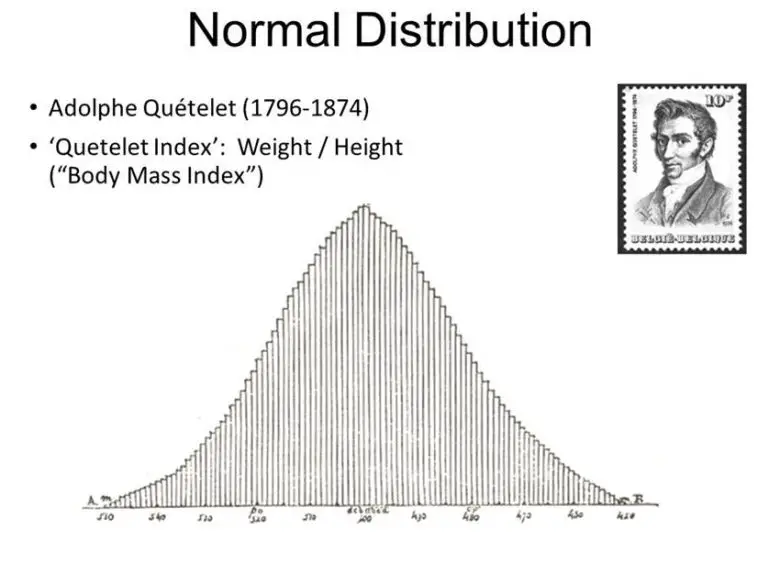
Bu esnada akla elbette akla normal nedir sorusu da gelecektir. Bir zamanlar matematikçi Carl Gauss ortalama bir ölçümün, bir ölçümün gerçek değerine oldukça yakın olduğunu göstermişti. Adolphe Quetelet ise normalin ne olduğunu tanımlamıştı.
Quetelet, veri alabileceği her insan özelliğinin ortalamasını hesaplamaya başladı. Ortalama boy, ortalama ağırlık ve ortalama ten rengini hesapladı. Çiftlerin ortalama yaşını ve insanların ortalama ölüm yaşını hesapladı. Günümüzde ortalamalara alışığız. Ancak Quetelet yeni bir ortalamayı her açıkladığında o zamanlarda halk şaşkına dönmüştü. Quetelet 1874 yılında öldü ancak onun fikirleri nesiller boyu devam etti. Günümüzde hepimiz ortalamanın içinde yer almaya çalışıyoruz. Bu dürtüyü Adolphe Quetelet’in araştırmalarına borçluyuz.
Kaynaklar ve İleri Okumalar
- Ask Ethan: Why does nature always follow a Bell curve? ; Bağlantı: Ask Ethan: Why does nature always follow a Bell curve? – Big Think ; Yayınlanma tarihi: 16 Şubat 2024
- Maths in a minute: The normal distribution; Kaynak site: Plus Math. Yayınlanma tarihi: 7 Ocak 2022; Bağlantı: Maths in a minute: The normal distribution
- Introduction To The Normal Distribution (Bell Curve). Yayınlanma tarihi: 11 Ekim 2023. Kaynak site: Simplypsychology. bağlantı: Introduction To The Normal Distribution (Bell Curve)
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel








