Kendimize büyük ölçüde düz çizgilerle çevrili bir dünya inşa ettik. Yaşadığımız evler, çalıştığımız gökdelenler, yürüdüğümüz sokaklar hep bu düz çizgilerin ve dik açılı yapıların içinde yer alıyor. Ancak bu düzenli, köşeli yapılar doğanın sunduğu geometriyle pek örtüşmez. Doğanın kendi dili farklıdır. Örneğin mercanlar, doğrudan hiperbolik geometri dediğimiz kavramın biyolojik karşılığı gibidir.

Doğa, yüz milyonlarca yıldır hiperbolik formlarla varlık gösterirken, matematikçiler bu tür yapıların imkânsız olduğunu kanıtlamaya çalışarak yüzyıllar harcadılar. Çünkü hiperbolik geometri, o döneme kadar değişmez kabul edilen Öklid geometrisinin temel aksiyomlarından birine karşı geliyordu.
Bu nedenle uzun süre boyunca radikal bir fikir olarak görüldü. Ancak bilimsel gerçekleri görmezden gelmek kolay değildir. Sonunda hiperbolik geometri kabul gördü ve bu, matematik tarihinde büyük bir zihinsel dönüşüme, adeta bir devrime neden oldu.
Günümüzde “geometrinin babası” olarak anılan Öklid, kendisinden önce gelen Thales, Pisagor ve Eudoxus gibi matematikçilerin çalışmalarını temel alarak Elementler adlı eserini yazdı. Bu kitap, sistematik olarak düzenlenmiş tanımlar, aksiyomlar ve teoremler içeriyordu ve 19. yüzyıla kadar akademik dünyada temel ders kitaplarından biri olarak kullanıldı.

Hiperbolik geometri neden radikal bir fikirdi?
Öklid’in aksiyomlarından biri, tüm üçgenlerin iç açılarının toplamının 180 derece olduğunu söylemekle eşdeğerdir. Bu, Beşinci Postulat olarak bilinir. Yüzyıllar boyunca matematikçiler, bu postulatın ilk dört aksiyomdan türetilebileceğini kanıtlamaya çalıştı. Ancak tüm bu çabalar sonuçsuz kaldı. Buna rağmen Öklid geometrisi, uzun süre boyunca matematikte baskın anlayış olarak varlığını sürdürdü.
Beşinci postulatın temel sorusu şudur: Düz bir çizgiye ve bu çizginin dışında bir noktaya sahibim. Bu noktadan geçip, orijinal çizgiyle hiç kesişmeyen kaç tane düz çizgi çizebilirim? Öklid’in yanıtı açıktı: Sadece bir tane. Ve bu cevap, sezgisel olarak çoğu kişiye doğru geliyordu.
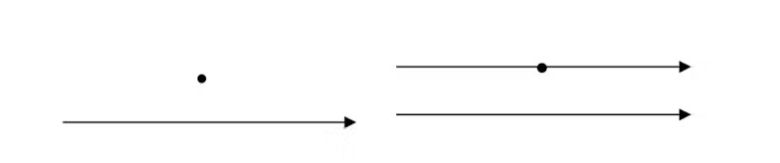
Ancak matematikçiler, bu postulatın gerçekten diğer aksiyomlardan türetilebileceğini kanıtlamakta ısrarcıydı. Yüzyıllar süren denemeler sonuç vermedi. Sonunda, Carl Friedrich Gauss (1777–1855), János Bolyai (1802–1860) ve Nikolai İvanoviç Lobaçevski (1793–1856) gibi matematikçiler, bu postulatın aksine dayanan ama yine de tutarlı olan Öklid dışı geometrileri geliştirdiler. Bu çalışmalar, matematikte yeni bir çağın başlamasına zemin hazırladı.
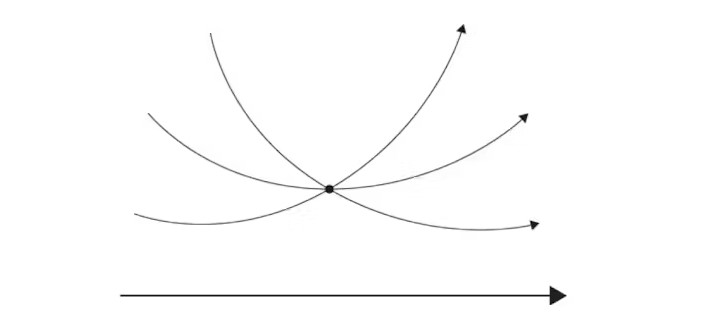
Matematikçiler János Bolyai ve Nikolay Lobaçevski, birbirlerinden tamamen bağımsız olarak beşinci postulatı gerektirmeyen farklı bir geometri türünün mümkün olabileceğini keşfettiler. Bugün bu keşif, hiperbolik geometri ya da Lobaçevski geometrisi olarak adlandırılır.

Bu yaklaşım, Öklid’in paralellik varsayımını reddeder ve düz bir çizginin dışındaki bir noktadan, o çizgiyle kesişmeyen birden fazla doğru geçebileceğini kabul eder. Bu çığır açıcı fikir, matematikte köklü bir dönüşümün kapısını aralamıştır.
Hiperbolik Geometri Nedir?
Farklı geometri türlerini anlamanın en iyi yollarından biri, yüzeylerin eğriliğini incelemektir. Düz, yani Öklid düzleminin eğriliği sıfırdır. Küre yüzeyi — örneğin bir plaj topu — pozitif eğriliğe sahiptir. Hiperbolik düzlem ise negatif eğrilik gösterir. Bu farklı eğrilikler, her geometri türünde farklı kuralların geçerli olmasına neden olur.
Bu üç geometrinin özellikleri birbirinden belirgin şekilde ayrılır. Örneğin, Öklid geometrisinde her üçgenin iç açılar toplamı tam olarak 180 derecedir. Ancak küresel geometride bu kural geçerli değildir. Bir kürenin yüzeyine üç nokta yerleştirilirse, bu noktaların oluşturduğu üçgenin iç açılar toplamı 180 dereceden fazla olur.
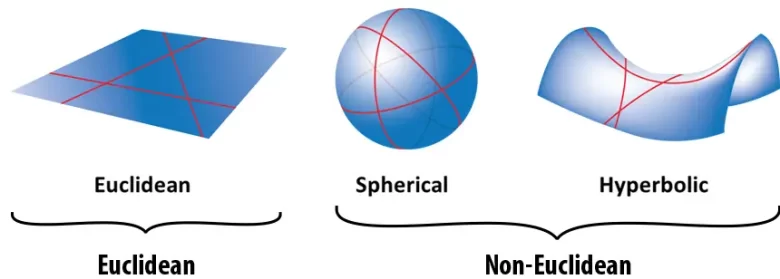
Hiperbolik geometride ise durum tam tersidir: Üçgenlerin iç açılar toplamı her zaman 180 dereceden daha küçük, ancak pozitif bir sayı olur. Bu farklılıklar, yüzeyin eğriliğinin geometriyi nasıl temelden etkilediğini gösteren çarpıcı örneklerdir.
Açı toplamının 180 dereceyi aşması ya da bu değerin altına düşmesi, Öklid’in hiç düşünmediği geometri türlerinin varlığını ortaya koydu. Bu keşif, yalnızca soyut matematikle sınırlı kalmadı; fizik, bilgisayar grafikleri, algoritma tasarımı gibi pek çok alanda somut uygulamalara dönüştü. Aşağıdaki şekilde yer alan tüm siyah beyaz desenler, hiperbolik üçgenleri temsil eder.

Hiperbolik şekiller, özellikle yüzey alanını maksimize etmenin avantaj sağladığı durumlarda ideal çözümler sunar. Ancak bu geometrik yapıları gerçek dünyada görselleştirmek kolay değildir. Bu soruna yaratıcı bir çözüm, matematikçi Daina Taimina tarafından geliştirildi. Taimina, hiperbolik düzlemleri tığ işi ile örerek somut bir biçimde temsil etti.

Evrenimizin Şekli Nasıldır?
Hiperbolik geometri, ilk bakışta yalnızca soyut ve hayali bir matematiksel yapı gibi görünmektedir. Bu yüzden, gerçek dünyada işe yaramayacağını düşünebilirsiniz. Ancak bu düşünce yanlıştır. Matematikçilerin farklı geometrik uzayların mümkün olduğunu fark etmesiyle birlikte, şu temel soru ortaya çıktı: Evrenimizin geometrisi hangisidir?
Galileo Galilei ve Isaac Newton, modern fiziğin temellerini atarken uzayın Öklid geometrisine uygun olduğunu varsaydılar. Ancak Albert Einstein’ın genel görelilik teorisi, evrenin düz değil, kavisli olabileceğini ortaya koydu. Einstein’ın denklemleri, uzayın kütle ve enerjiye bağlı olarak bükülebileceğini ve dolayısıyla Öklid dışı formların fiziksel olarak mümkün olduğunu gösterdi.
Bugün gökbilimcilerin üzerinde çalıştığı en büyük sorulardan biri, evrenin şeklinin ne olduğudur. Büyük ölçekli gözlemler genellikle düz, yani Öklid yapılı bir evreni destekler gibi görünse de, hiperbolik (negatif eğrilikli) bir evrende yaşadığımıza dair ipuçları da bulunmaktadır. Yani hiperbolik geometri, yalnızca teorik bir model değildir.
Kaynaklar ve ileri okumalar:
- Maths in a minute: Not always 180. Yayınlanma tarihi: 3 Temmuz 2013; Kaynak site: Plus Math. Bağlantı: Maths in a minute: Not always 180
- Corals, crochet and the cosmos: how hyperbolic geometry pervades the universe. Yayınlanma tarihi: 27 Ocak 2016. Kaynak site: Conversation. Bağlantı: Corals, crochet and the cosmos: how hyperbolic geometry pervades the universe
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel






