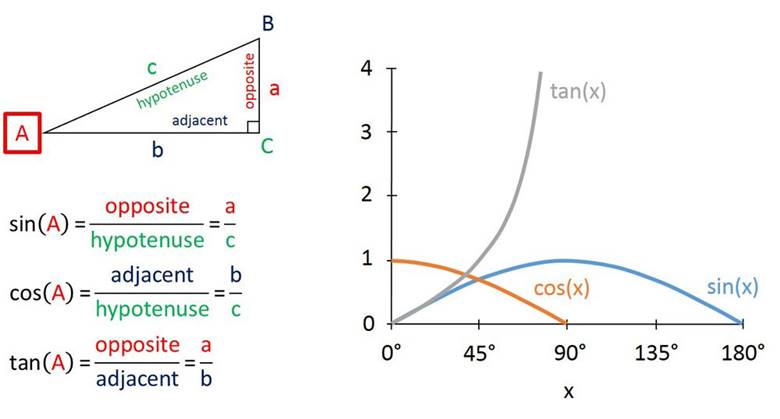
Trigonometri Nedir? Sinüs İle Kosinüs Tam Olarak Ne Anlama Gelir?

Trigonometri, üçgenlerin kenarları ve açıları arasındaki ilişkileri inceleyen matematiğin bir dalıdır. Bir çok şeklin üçgenlere ayrılması mümkün olduğu için geometri ile uğraştığımız hemen her an, bir biçimde karşımıza çıkar.

Dahası trigonometriyi, geometri ile uğraşmadığınız zamanlarda da kullanmak zorunda kalacaksınız. Karmaşık sayılar, sonsuz seriler, logaritma ve kalkülüs ile uğraştığınız zamanlarda da çözüm esnasında bir biçimde işin içine karışacaktır.  

Trigonometri ile tanıştığımız anda karşımıza kulağa yabancı gelen üç kelime daha çıkar: Sinüs, kosinüs ve tanjant. Sözlük karıştırmayı seven biri bu kelimeleri araştırırsa tanjant kelimesine karşılık” teğet” yazıldığını görecektir. Ancak sinüs ve kosinüs tam olarak nedir? Bu sorulara cevap için öncelikle “trigonometri nedir?” sorusuna cevap vermek gerekli.

Trigonometri Nedir?

Trigonometri dediğimiz zamanlarda da ilk öğrendiğimiz bilgi aşağıdaki gibidir. Ancak modern trigonometri anlayışımız, gök cisimlerinin gece gökyüzündeki hareketini inceleyen eski Yunan astronomlarına kadar uzanır. Zaten, Trigonometri kelimesi de, Yunanca üçgen ( trigōnon ) ve ölçü ( metron ) kelimelerinden gelir.

Güneş Ay’dan ne kadar uzaktadır ve ne kadar büyüktür? Ve eğer bir teleskopu bile olmayan, antik Yunan’da araştırmalar yapan bir kişiyseniz bu gibi sorulara nasıl cevap verirsiniz? Günümüzden 2300 yıl önce yaşamış olan Sisamlı Aristarkus bu sorulara bir cevap bulmayı başarmıştı.

Güneş’in Ay’ı aydınlattığı bilgisine sahip olan Aristarkus, yarım Ay’da Dünya, Ay ve Güneş’in oluşturduğu üçgenin Ay noktasında dik açı yaptığını fark etti. Artık Φ açısını ölçerek ve trigonometri kullanarak Dünya’dan Ay’a, Dünya’dan Güneş’e olan mesafeye hesaplamak mümkündü.

Babilliler de Yunan astronomlarından yaklaşık 1000 yıl önce trigonometrinin öncülü kabul edeceğimiz bazı çalışmalar yapmışlardı. Ancak okullarda öğrendiğimiz trigonometrinin ilk izleri karşımıza M.Ö. 120’de yaşamış olan Yunan gökbilimci İznikli Hipparkhos’un çalışmalarında çıkar. 

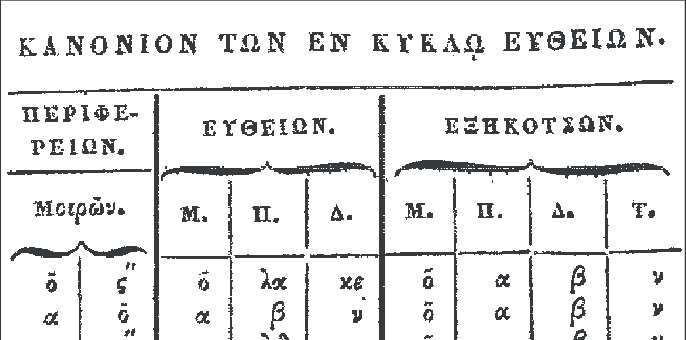
Hipparkhos açıların yaylarla değil kirişlerle ölçülmesi gerektiğini ileri sürmüştü. Farklı açılara karşılık gelen kirişlerin uzunluklarını veren bir tablo hazırlamış ve bunu sistematik olarak kullanmıştı. Kirişler tablosundaki değerler günümüzde kullandığımız sinüs fonksiyonunun değerlerine yaklaşık olarak denk gelmektedir.

Sinüs Ve Kosinüs Nedir?

Tarihsel olarak, Hindistan’ın kendine ait zengin bir matematik geleneği olmuştur. Ve bariz bir nedenden dolayı trigonometri tam da onun merkezinde yer alır. Hintli matematikçiler de temelinde astronomik araştırmaları kolaylaştırmak amacıyla trigonometriyi kullanmışlardı. İlgili trigonometrik terimler için de okçulukta kullanılan yaydan esinleneceklerdi.

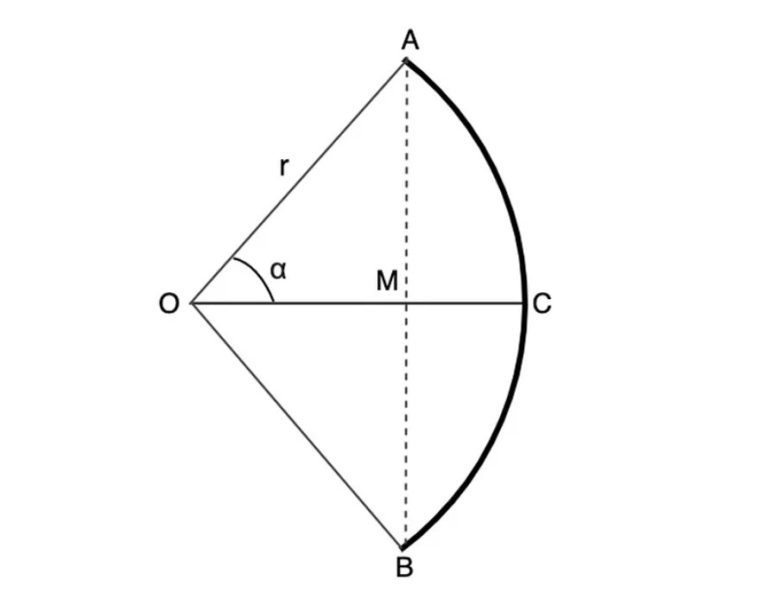
Kiriş, bir çizgi parçasını bir açı ile ilişkilendirmenin en basit yolu olsa da, birçok durumda kullanılması gereken aslında açının yarısıdır. Bu sayede elimizde dik üçgenler olur. Hintli gökbilimciler bunu anlamışlardı. Bu nedenle kirişleri tablo haline getirmektense kirişlerin yarısını tablo haline getirmişler ve yarı kirişler tablolarını hesaplamak için karmaşık yöntemler geliştirmişlerdi.

Hint terminolojisinde kiriş kelimesi samastajya olarak adlandırılırdı. Burada samasta tam anlamına, jya ise yay anlamına gelir. Yarı kiriş ise (AM veya MB), ardhajya demektir ve jya biçiminde kısaltılmıştı. Bu aslında dönemin Hintli matematikçilerinin sinüse verdikleri isimdi. Aşağıdaki görselde ise yay ve ok sistemini kullanarak trigonometrik kavramları temsil etmenin Hint yolunu görüyorsunuz.

İslam Dünyasının Trigonometriye Katkısı Nedir?

Latince adı Albategnius olarak bilinen Al-Battani, MS 858’de Urfa’nın Harran bölgesinde doğmuş bir astronom ve matematikçiydi. “Arapların Batlamyus’u” olarak da anılan Battani, Ortaçağ İslam dünyasının en iyi bilinen astronomudur.

Battani hakkında yazılı bilgiler sınırlıdır. Ancak bazı belgeler, onun hassas ölçümler yaparak elde ettiği verilerin yüzyıllarca Avrupalı astronomi uzmanlarına ışık tuttuğunu göstermektedir. Önemli buluşlarından biri Dünya’nın Güneş etrafında dönerken dairesel bir yörünge izlemediğini fark etmesidir. Onun çalışmalarının Tycho Brahe, Kepler, Galileo ve Kopernik gibi bilim insanları üzerinde büyük etkisi olmuştur.

Battani, çalışmaları sırasında bazı temel trigonometrik bağıntılara ulaşmış ve bunları astronomik hesaplamalarda kullanmıştır. Ayrıca sıfırdan 90 dereceye kadar açıların trigonometrik değerlerini de hesaplamıştı. Bu nedenle Battani Batı’ya trigonometriyi öğreten kişi olarak bilinir. 

Battani’ni yaptığı kirişler tablosunu, günümüzde kullandığımız trigonometrik ifadeler ile değiştirmesiydi. Bu nedenle sinüs, kosinüs, tanjant, kotanjant, sekant ve kosekantı gerçek anlamda ilk defa kullanan kişi o oldu.

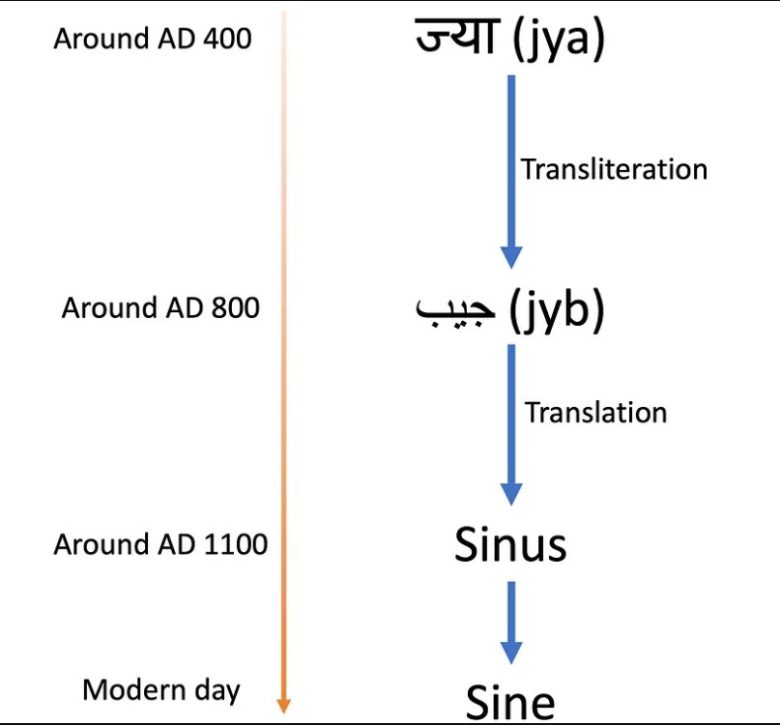
Bilgi Avrupalı ​​matematikçilere geçtiğinde Arapça eserler tercüme edilmeye başlandı. Latince çevirmenler jyb kelimesini jaib olarak yanlış anladılar. Bu yaka açıklığı gibi bir anlama gelmektedir. Bu nedenle modern zamanda sinüs aslında bu anlama gelmektedir. Aşağıdaki görselde sinüs kelimesinin değişimini görüyorsunuz.

Tam 200 yıl, kosinüs için özel bir ada ihtiyaç duyulmadı. Zaman içinde de tamamlayıcı açının sinüsü anlamına gelen co-sinüs ifadesi kullanılmaya başlandı.

Trigonometri Ne İşimize Yarıyor?

Öğrencilik hayatımız boyunca sinüs fonksiyonunu geometri problemlerini çözerken bir çoğumuz öğrendik. Ancak bir dik üçgende belli bir oran olarak tanımlamaya alışık olduğumuz sinüs bundan çok daha fazlasını yapar.

Ne kadar karmaşık olursa olsun, herhangi bir dalga biçimini (dinlediğiniz müzik, Wi-Fi üzerinden gönderdiğiniz dijital sinyal, hatta denizdeki dalga) oluşturmak için kullanılabilir. Hatta bu nedenle de Sinüs dalgası veya sinüzoid doğal salınım dalgası olarak kabul edilmektedir.

Peki bir birim çemberin çevresinde hareket ettiğinizde sinüs fonksiyonuna ne olur? Bu durumda çemberin etrafından bir tur atarsanız 360 derece diğer deyişle 2π radyanlık bir açıyla dönmüş olacaksınız. Çemberin etrafında hareket ettikçe dikey koordinatınız (sinüs) 0’dan başlar. Çemberin tepesindeyken maksimum değerini alacağı 1’e ulaşana kadar istikrarlı bir şekilde artar.

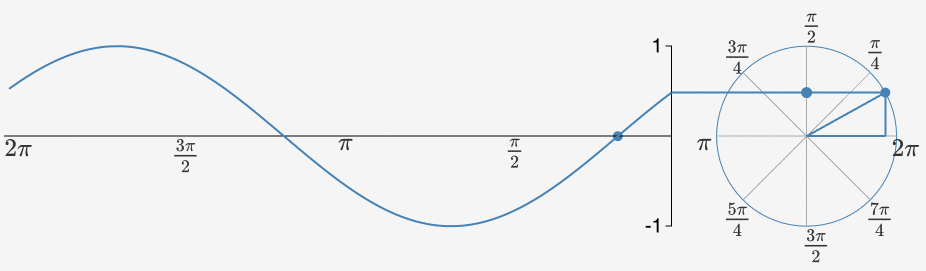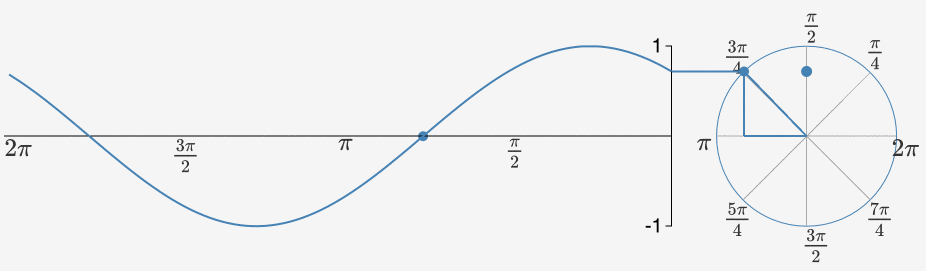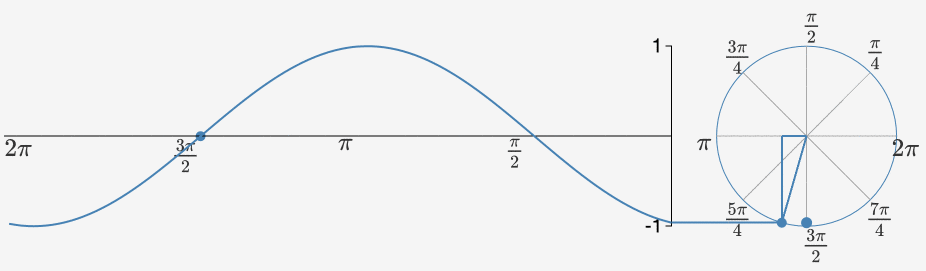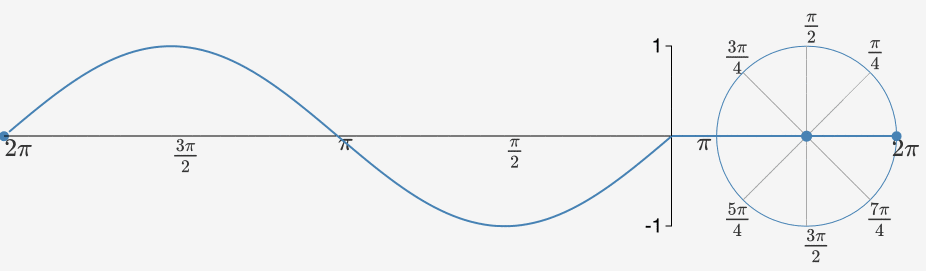
Hareket etmeye devam ettikçe simetrik bir şekilde tekrar 0’a düşer ve ardından minimum değeri olan -1’e ulaşır. Sonunda da tekrar 0 oluncaya kadar artar. Çember etrafında dönmeye devam ettikçe de sonsuz uzunlukta, kusursuz biçimde düzenli bir dalga elde edersiniz.

Bu sinüs ve kosinüs dalgaları, gerçek hayatta karşılaştığımız dalgalar hakkında size pek bir şey anlatamayacak kadar mükemmel görünüyor. Ancak herhangi bir ses dalgasını çeşitli frekans ve genliklere sahip bir dizi sinüs dalgasına bölmek mümkündür.  

Bir ses dalgasının veya zaman içinde değişen herhangi bir sinyalin kendisini oluşturan sinüs dalgalarının toplamı olarak ifadesi, o sinyalin Fourier dönüşümü olarak bilinir. Bu dönüşüm ise “trigonometri nedir ve ne işe yarar?” sorusuna verebileceğimiz bir örnektir.

Kaynaklar ve ileri okumalar:

• The Sun, the Moon and trigonometry. Yayınlanma tarihi: 1 Eylül 2014. Kaynak site: Plus Math Bağlantı: The Sun, the Moon and trigonometry
• The Etymology of Sine. Bağlantı: https://www.cantorsparadise.com/
• How ancient Babylonian land surveyors developed a unique form of trigonometry. 1,000 years before the Greeks. Yayınlanma tarihi: 4 Ağustos 2021. Bağlantı How ancient Babylonian land surveyors developed a unique form of trigonometry. 1,000 years before the Greeks./

Size Bir Mesajımız Var!

Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.

Matematiksel