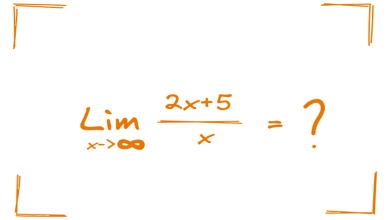Elipsin çevresini kesin bir formülle ifade etmek mümkün değildir. Bu zarif geometrik şeklin çevresini hesaplamak, matematiğin en karmaşık ve çözülemeyen problemleri arasında yer alır. Bu durum, elipsin çevresini teorik ve pratik düzlemde ilgi çekici bir konu haline getirmiştir.

Elipsin alanını hesaplamak oldukça basittir. Ancak çevre söz konusu olduğunda işler değişir. Bir elipsin çevresini hesaplamak, bir çemberin çevresini hesaplamaktan çok daha karmaşıktır. Dairenin çevresi için basit bir formül olan C=2πr varken, elips için böyle bir kesin formül yoktur. Bunun yerine, bir elipsin çevresi aşağıdaki integral ile gösterilmektedir.
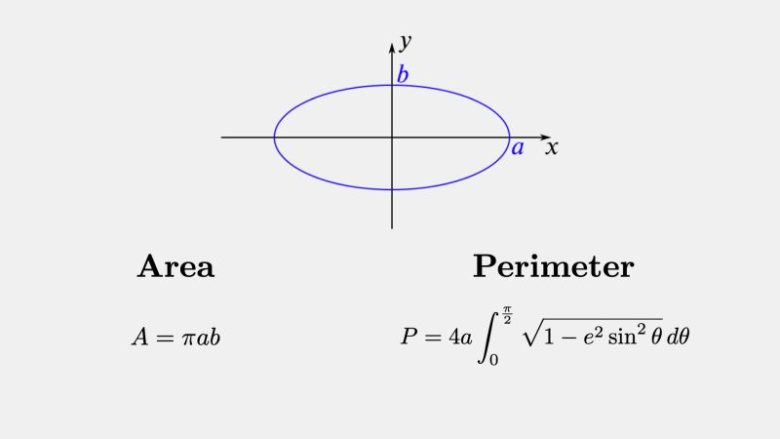
Bu integralin çözülmesi oldukça karmaşıktır ve elipsin çevresini hesaplamaya çalışmak, bu karmaşıklık nedeniyle matematikte başlı başına bir meydan okuma haline gelmiştir. Bu tür integral, eliptik integral olarak bilinmektedir ve matematikte özel bir yere sahiptir.
Eliptik integral Nedir?
Eliptik integral, genellikle elips ve eliptik eğrilerle ilişkili olan özel bir integral türüdür. Bu integraller, standart matematiksel fonksiyonlarla (örneğin, polinomlar, trigonometrik veya üstel fonksiyonlar) ifade edilemez.
Eliptik integraller, birinci tür ve ikinci tür olmak üzere farklı sınıflara ayrılır. Her birinin kendine özgü matematiksel yapısı vardır. Bu durum, eliptik integralin çözümünü daha karmaşık hale getirir ve bu karmaşıklık elipsin çevresi problemini, matematiğin çözülemeyen problemlerinden biri olarak tanımlar.
Eliptik integrallerin kesin çözümleri mümkün olmadığı için, elipsin çevresi yalnızca yaklaşık değerlerle hesaplanır. Bu zorluk, matematikçiler için hem bir meydan okuma hem de ilgi çekici bir araştırma alanı yaratmıştır.
Elipsin çevresini kesin olarak hesaplamak mümkün olmasa da, Hintli matematikçi Srinivasa Ramanujan, yüksek doğruluk seviyesine sahip yaklaşık formüller geliştirmiştir. Ramanujan’ın formülleri, mühendislik ve astronomi gibi alanlarda pratik uygulamalarda sıkça kullanılmıştır.
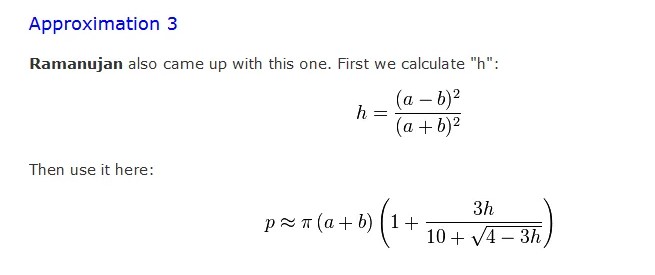
Elipsin çevresi için kesin bir formülünü bulma çabası, 18. yüzyılda eliptik fonksiyonların keşfine yol açmıştır. Bu fonksiyonlar, genellikle elipslerle ve eliptik eğrilerle ilişkili matematiksel problemleri çözmek için geliştirilmiştir. Bu fonksiyonlar, eliptik integrallerin ters fonksiyonları olarak tanımlanır ve matematiğin karmaşık analiz, cebirsel geometri ve sayı teorisi gibi birçok alanında önemli bir yer tutar.
Eliptik fonksiyonlar, iki farklı yönde periyodik yapıya sahiptir. Bu özellik, karmaşık düzlemde düzenli bir desen oluşturmalarını sağlar ve sayı teorisi gibi alanlarda kritik bir rol oynar. Modüler dönüşümlere göre değişmezlik gösteren bu fonksiyonlar, matematiğin temel yapı taşlarından biridir.
Euler, Gauss, Abel ve Jacobi gibi büyük matematikçilerin çalışmaları sayesinde eliptik fonksiyonlar, yalnızca elipsin çevresi problemi için değil, aynı zamanda karmaşık matematiksel problemlerin çözümünde genel bir araç haline gelmiştir.
Elipsin Çevresini Hesaplamak Neden Önemlidir?
Elipsin çevresi problemi, yalnızca teorik bir matematiksel ilgi alanı değil, aynı zamanda gerçek dünyada geniş bir uygulama yelpazesine sahiptir. Bu zarif geometrik şekil, astronomi, fizik, optik ve mühendislik gibi alanlarda temel bir role sahiptir.
Gezegenlerin yörüngeleri elips şeklindedir ve bu yörüngelerin dinamiklerini anlamak, elipsin çevresinin doğru bir şekilde hesaplanmasını gerektirir. Kepler’in gezegen hareket yasaları, elipsin astronomideki önemini vurgular. Gezegenlerin hareket dinamiklerini analiz etmek ve yörüngeleri tanımlamak için elips geometrisine dayanan matematiksel çözümler kullanılır.
Fizik ve optik alanlarında da elipsin etkisi büyüktür. Işığın yansıması ve kırılması gibi olaylar elips geometrisini temel alır. Özellikle, eliptik aynalar ışığı odaklamak ve yönlendirmek için yaygın olarak kullanılırken, optik sistemlerdeki mercek tasarımları da elipsin geometrik özelliklerinden faydalanır. Teleskoplar, kameralar ve mikroskoplar gibi cihazların tasarımında elips, ışık yayılımının kontrolü için vazgeçilmez bir araçtır.
Mühendislikte ise elips, yapı tasarımı ve mekanik sistemlerde önemli bir yer tutar. Elipsin geometrik özellikleri, hem estetik hem de dayanıklılık açısından kubbeler ve köprüler gibi mimari yapılarda tercih edilir. Mekanik sistemlerde ise eliptik hareketlerin modellenmesi, titreşim analizlerinden motor tasarımına kadar pek çok uygulamada kullanılır.
Sonuç Olarak
Elipsin çevresi, matematik dünyasında çözümü zor, ancak bir o kadar da ilgi çekici bir problem olarak varlığını sürdürmektedir. Bu problem, basit bir geometrik şeklin ardında nasıl bir karmaşıklık ve derinlik barındırabileceğini gözler önüne serer.
Kaynaklar ve ileri okumalar
- Why is there no equation for the perimeter of an ellipse‽. Yayınlanma tarihi: 5 Eylül 2020. Kaynak site: Youtube. Bağlantı: Why is there no equation for the perimeter of an ellipse
- Villarino, Mark. (2005). Ramanujan’s Perimeter of an Ellipse.
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel