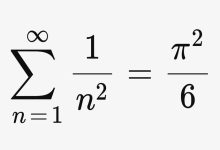John Nash’in 1950’de yayınladığı iki sayfalık makale, Oyun Teorisi alanına ve stratejik karar verme konusundaki genel anlayışımıza ufuk açıcı bir katkı sağladı. Kendisi bu makalesinde Nash dengesi olarak bilinen bir temel kavramı ortaya koydu.
Karşısındakini yok etmek ile tehdit eden iki ülke düşünün. Bunlardan biri, düşmanını hedef almış ve ordusunu füzelerle donatıyor. Diğeri de o öyle yaptığı için aynısını yapıyor. Her bir ülke, silah satın alarak diğeri üzerinde üstünlük kurmaya çalışıyor.
Bu silahlanma yarışı sonucunda ikisi de, birbirine yöneltilmiş, devasa bir füze stokuna sahip oluyor. Her iki tarafın da, düşmanının ne yapabileceğini hesaba katarak, ne yapacağına karar vermesi gerekir. Oyun teorisyenleri buna “stratejik etkileşim” der. Bu tarz etkileşimler oyun teorisi kapsamında incelenir. Oyun teorisi, taş-kağıt-makas oyunu gibi basit oyunlardan tutun da, iş adamlarının kar arayışına ve uluslar arasındaki savaşlara kadar her yerde karşımıza çıkan stratejik etkileşimleri araştırır.
Oyun Teorisi Nedir?
En basit anlamıyla oyun teorisi, akıllı karar vericiler arasındaki çatışma veya işbirliği modellerinin incelenmesidir. Karınca kolonilerinin işleyişinden, tüketicilerin satın alabilecekleri ürünlere kadar her şey bu matematiksel çerçeveyle açıklanmıştır.

Yukarıda örnek olarak verdiğimiz silahlanma yarışı süreci gerçektir. Bu durum İkinci Dünya Savaşı sonrasında, Amerika Birleşik Devletleri ile Sovyetler Birliği arasında yaşanmıştır. Soğuk Savaş dönemin de Amerikan ordusu, ulusal güvenliğe yardımcı olacak alanlarda yapılacak araştırmalar için ödenek ayırmıştı. Oyun teorisi de bu alanlardan biridir.
Bu süreçte bir çok matematikçi, askeri bir araştırma örgütlenmesi olan RAND (research and development) Corporation’ da görev aldı. J. Robert Oppenheimer’ın meslektaşlarından biri olan dahi Macar matematikçi John von Neumann bunlardan biri idi.

Kendisi, Los Alamos’ta Nagasaki bombası üzerinde çalışmakla kalmadı, aynı zamanda ekonomi ile ilgilenmeye başladı. Sonunda ilk saldırı nükleer saldırılarını ikinci aşamadaki misillemelere karşı test etmek için kullandığı oyun teorisini geliştirdi. Ayrıca bu nükleer ve ekonomik “oyunların” simülasyonlarına olanak tanıyan bilgisayar mimarisini de oluşturdu.
John Nash’in Oyun Teorisine Katkısı Nedir?
Oyun teorisi, 1944 yılında “Oyun Teorisi ve Ekonomik Davranış”ın yayınlanmasıyla resmen dünyaya girdi. Bu, Avusturyalı bir ekonomist olan Oskar Morgenstern ile Neumann arasındaki işbirliğinin sonucuydu.

Oyun teorisi kararların etkileşime girdiği durumlarla ilgilidir. Bu tür durumlar gerçek hayatta karşımıza çıkar. Örneğin bir açık artırmada bir alıcının kazancı yalnızca onun teklif ettiği miktara değil aynı zamanda diğer alıcıların tekliflerine de bağlıdır.
Benzer biçimde bir firmanın elde ettiği kâr, sadece kendi ürünü için belirlediği fiyata değil aynı zamanda rakiplerinin belirlediği fiyatlara da bağlıdır. Bir tenis maçında servis atan oyuncunun sayı kazanma olasılığı, servisi karşılayanın soluna mı yoksa sağına mı attığına ve karşılayanın servisi doğru tahmin edip etmediğine bağlıdır.
Bunların hepsi, matematikçilerin ve ekonomistlerin “oyun” olarak adlandırdığı “işbirlikçi olmayan” stratejik etkileşimlerin örnekleridir. Karar vericiler eylemlerini bağımsız olarak aldıkları için de işbirlikçi değildirler. Yani eylemler ile ilgili anlaşmalar yapılması olası değildir.

Nash’in oyun teorisi alanındaki çalışmaları 1950’de Princeton Üniversitesi tarafından verilen doktorasıyla başladı. Nash’den önce bu alan, belirli tip sorunlar ile ilgiliydi. Von Neumann, oyunların sonucunu bulmak için bir yöntem geliştirme konusunda büyük bir aşama kaydetmişti. Ama bu yöntem yalnızca bazı durumlarda, örneğin katılımcıların müzakere edebildikleri ve birbirleriyle sağlam anlaşmalar yapabildikleri durumlarda işe yarıyordu.
Dolayısıyla oyuncuların birbirlerine verdikleri herhangi bir söze zorunlu olarak bağlı kalmayacakları türden oyunlar da dahil, başka oyunlarda da işleyecek bir yönteme ihtiyaç vardı. Nash’in oyun teorisine en temel katkısı, alanı üzerinde çalışılacak farklı senaryolara açmasıydı. Disiplini dar olan odağının dışına çıkardı. Sonucunda onun bu katkısı olmasaydı, oyun teorisinin bugünkü popülerliğini kazanması olası olmayacaktı.
Nash Dengesi Nedir?
Nash’in 1950 tarihli makalesinde geliştirilen Nash dengesi kavramı, ekonomistlerin stratejik etkileşimlerin sonuçlarını tahmin etmesinin temelini oluşturdu. Nash’in dediğine göre, oyunun sonucu, yani “denge”si, her bir oyuncunun öteki oyuncuların da aynı şeyi yaptığı ortamda kendisi için en iyisini yapmasıdır. Herkes bunu yaptığında, hiç kimsenin yaptığı şeyi değiştirmesi için bir nedeni olmaz; dolayısıyla bu, oyunun dengesi olur. Bu denge durumuna da Nash dengesi denir.
Kavşağa yaklaşan bir sürücüyü düşünün. Kırmızı ışığa yaklaştığında durur, yeşil ışığa yaklaştığında ise yoluna devam eder. Tüm sürücülerin bu şekilde davranması bir Nash dengesidir. Kırmızı ışığa yaklaşırken durmak ve yeşil ışığa yaklaştığında devam etmek herkes için en iyisidir. Bu nedenle dengede kendi rolünü oynamak her sürücünün kendi çıkarınadır.
Nash dengesi aynı zamanda karar vericilerin rastgele stratejiler izlemesi ihtimaline de izin verir. Bu oyun teorisinin matematiği açısından önemlidir çünkü her (sonlu) oyunun bir Nash dengesine sahip olduğunu garanti eder. Örneğin, Taş-Kağıt-Makas oyununu düşünelim. Hepimiz kendi deneyimlerimizden, Taş-Kağıt-Makas oyununun nasıl oynanacağını biliyoruz. Bu oyunda kazanma ya da kaybetme geçmiş oyunlardaki eylemlerden ve sonuçlardan bağımsızdır. Aslında Nash dengesinin öngördüğü şey de tam olarak budur.
Nash’in teorisi herhangi sayıda karar vericinin olduğu herhangi bir oyun için geçerliyken, John von Neumann’ın 1928 Minimax Teoremi yalnızca iki oyunculu “sıfır toplamlı” oyunlar için geçerlidir. ( Bir oyuncunun kazancı diğer oyuncunun kaybı olursa buna sıfır toplamlı oyun denir.)
Nash’in çalışması, her karar vericinin diğerlerinin eylemlerini bilmeden kendi eylemini gerçekleştirdiği ve hiçbir karar vericinin özel bilgiye sahip olmadığı oyunlarla ilgiliydi. İlerleyen süreçte John Harsanyi, Nash dengesi kavramını ele aldı.
Karar vericilerin özel bilgilere sahip olduğu müzayedeler gibi stratejik etkileşimleri ele alacak şekilde genişletti. Reinhardt Selten ise, Nash dengesi kavramını, bir veya daha fazla karar vericinin kendi eylemini gerçekleştirmeden önce diğerinin eylemini gözlemlediği dinamik etkileşimleri ele alacak hale getirdi.
Sonuç olarak

Nash bu fikirlerini, henüz genç bir adamken yazdığı bir dizi matematik makalesinde ortaya koymuştu. Sonra Nash ortadan kayboldu. Ciddi bir zihinsel hastalıktan mustaripti ve on yıllar boyunca hastanede ve evinde tedavi görecekti. Ancak onun fikirleri yokluğunda ekonomide devrim yarattı.
Nash’in çalışmaları yalnızca modern ekonomide devrim yaratmakla kalmadı. Aynı zamanda bilgisayar bilimi, siyaset bilimi, sosyoloji ve biyoloji gibi çok çeşitli alanlarda da önemli bir etkiye sahip oldu. Nash, tüm bu katkılarından dolayı 1994 yılında Nobel Ekonomi Ödülünü Harsanyi ve Selten ile paylaştı. 2001 tarihli, A Beautiful Mind isimli filmde onun olağandışı hayat hikayesi anlatılır. İzlemediyseniz kaçırmamanızı öneririz.

Nash’in çalışması işbirlikçi olmayan oyunlara da uygulandı. Bu durumlarda oyuncular, diğer oyuncuları etkilemeden kendi sonuçlarını iyileştirmek (veya kötüleştirmek) için stratejiyi tek taraflı olarak değiştirebilirler. Buna bir örnek bu yazıda okumaya devam edebileceğiniz Mahkum İkilemi olacaktır.
Kaynaklar ve ileri okumalar
- Dominici, Gandolfo. (2011). Game Theory as a Marketing Tool: Uses and Limitations. Elixir Journal. 3524-3528.
- John Nash and his contribution to Game Theory and Economics. Yayınlanma tarihi: 26 Mayıs 2015. Kaynak site: Conversation. Bağlantı: John Nash and his contribution to Game Theory and Economics
- Sethi, Rajiv & Weibull, Jörgen. (2016). WHAT IS…Nash Equilibrium?. Notices of the American Mathematical Society. 63. 526-528. 10.1090/noti1375.
Matematiksel