Matematik ve müzik farklı alanlar gibi görünse de, aslında yüzyıllar öncesine dayanan derin bir bağa sahiptir. Bu nedenle, bu iki disiplinden birinde ustalaşmak, diğerinde de yetkinliğinizi artırabilir.

Matematiksel müziğin temel yöntem ve anlayışları, Antikçağ’dan günümüze kadar kademeli olarak gelişmiştir. Günümüzdeki yaklaşımların arkasındaki pek çok düşünce, farklı dönemlerde şekillenmiştir. Antikçağ’da, müziğin temel yapı taşlarını matematiksel olarak biçimlendirmeye yönelik ilk girişimlerle karşılaşırız.
Bu alandaki en bilinen örnek, Antik Yunan kuramcısı Pisagor’un mistik ve felsefi öğretisidir. Pisagor, müzikle pratik açıdan değil, onun bilimsel doğasıyla ilgilenmiştir. Matematiksel oranlarla müziksel aralıklar arasındaki ilişkiyi keşfeden ilk kişidir. Pisagorcu okul, müziği matematikle aynı düzeyde bir bilim olarak kabul etmiş; oranların incelenmesini, evrenin temelindeki sayısal yasaları anlamanın anahtarı olarak görmüştür.

Matematik Ve Müzik İlişkisi Nedir?
Ses, bir çalgı parçasının titreşmesiyle oluşur. Tel, kamış ya da deri gibi malzemeler titreştiğinde, çevredeki hava moleküllerini harekete geçirir. Bu hareket, zincirleme şekilde yayılır ve bir ses dalgası meydana gelir. Kulak, bu titreşimler kulak zarını etkilediğinde sesi algılar.
Bir dalganın frekansı Hertz (Hz) cinsinden ölçülür ve saniyedeki titreşim sayısını ifade eder. İnsan kulağı, yaklaşık 20 Hz (saniyede 20 titreşim) gibi çok düşük frekanslardan başlayarak, yaklaşık 20.000 Hz’e (saniyede 20.000 titreşim) kadar olan sesleri duyar.
Beynimiz bu aralığın en alt ucundaki tekil titreşimleri algılayamaz; bu yüzden onları “perde” olarak adlandırdığımız bir duyum şeklinde deneyimleriz. Örneğin, orta do’nun üzerindeki la sesi orkestralarda akort sesi olarak kullanılır ve frekansı 440 Hz’dir. Bu da yaylı, tahta üflemeli ve borulu çalgıların bir la sesi çaldığında, saniyede 440 temel titreşim içeren ses dalgaları ürettikleri anlamına gelir.
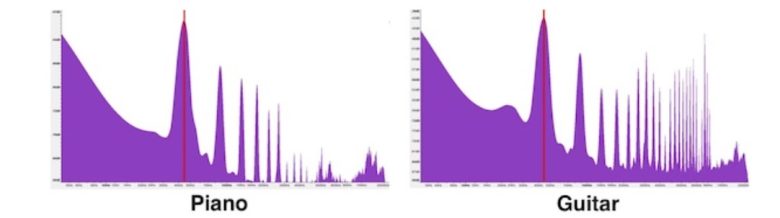
A4 notasını farklı çalgılarla çaldığımızı düşünelim. Bir çalgı bu notayı üretirken yalnızca 440 Hz’de titreşmez. Aynı anda, bu frekansın tam katları olan başka titreşimler de üretir. Bu ek titreşimlere harmonikler denir. Örneğin, 880 Hz ikinci, 1320 Hz üçüncü harmoniktir ve bu dizi bu şekilde sürer.
Buradaki önemli nokta, tüm çalgıların aynı harmonik frekanslara sahip olmasıdır. Ancak her çalgı bu harmonikleri farklı oranlarda üretir. Piyanoda bazı harmonikler ön plana çıkar; gitarda ise farklı harmonikler baskın hâle gelir. Aynı A4 notasının farklı çalgılarda farklı tınlamasının nedeni budur.
İki nota aynı anda çalındığında, kulak bu birlikteliğe rastlantısal bir tepki vermez. Bazı ses çiftleri kulağa dengeli ve uyumlu gelirken, bazıları gergin ve rahatsız edici bir izlenim bırakır. Bu farkı, notalar arasındaki frekans ilişkisi belirler.
Müzik, Matematik Ve Oranlar
Batı müzik geleneğinde majör ve minör diziler, hatta tüm modlar, frekanslar arasındaki tam sayı oranlarına dayanır. Aynı ilke, dünya müziklerinin büyük bölümünde de geçerlidir. İki notanın frekansları basit bir oran oluşturduğunda, ses dalgaları düzenli bir şekilde örtüşür; titreşimler birbirini destekler ve kulak bu birleşimi “uyumlu” olarak algılar.
Oran karmaşıklaştıkça durum değişir. Frekanslar artık basit katlar hâlinde örtüşmez; dalgalar düzensiz titreşimler üretir ve kulak bu yapıyı çözümlemekte zorlanır.
Tam sayı oranı, 2:1, 3:2, 4:3, 5:3 gibi iki tam sayı arasındaki ilişkiyle tanımlanır. Bu düşünceyi frekanslara uyguladığımızda, tam sayı oranına sahip iki sesi birlikte çalmış oluruz. Örneğin, 2:1 oranı 1000 Hz ile 500 Hz arasında, 3:2 oranı ise 600 Hz ile 400 Hz arasında kurulur. Bu ilke, müzik teorisinin temel taşlarından biridir.
Oktav, müzikte en temel aralıktır. Aynı notanın biri kalın, biri ince hâlidir. İnce olan ses, kalın olanın tam iki katı hızla titreşir. Bu yüzden frekans oranı 2:1’dir. nsan sesi, telli çalgılar ve borulu çalgılar, doğal olarak bu oranı üretir. Bu yüzden müzik kültürlerinin tamamına yakınında oktav temel oran olarak kabul görür.
Beşli (3:2)
Beşli aralık, temel notanın frekansının 1,5 katı olan bir sesle oluşur. Bu iki nota arasındaki frekans oranı 3:2’dir. Örneğin, do tonunda bu beşinci nota sol’dür. Piyanoda, do’dan başlayarak beyaz tuşlar üzerinde beş adım yukarı çıkıldığında bu notaya ulaşılır.
Bu aralık kulağa güçlü ve dengeli gelir. Bunun nedeni, frekanslar arasındaki basit sayısal ilişkidir. Üst notanın her üç titreşimine karşılık, alt nota iki titreşim üretir. Beşli aralık, oktavdan sonra müzikteki en kararlı aralıktır. Bu nedenle, ezgilerin inşasında ve armoninin oluşumunda merkezi bir role sahiptir.
Büyük üçlü (5:4) ve küçük üçlü (6:5)
Batı müziğinde akor, en az üç sesten oluşur: bir temel ses, onun beşlisi ve aradaki üçüncü ses. Bu üçüncü ses, armoninin karakterini belirler.
Üçüncü ses, temel sesten biraz daha uzaktaysa kulağa daha aydınlık bir etki verir. Bu yapıya büyük üçlü denir ve frekans oranı 5:4’tür. Yani üst ses, alt sesten biraz daha yüksek frekansta titreşir.
Üçüncü ses temel sese biraz daha yakınsa, daha karanlık bir etki oluşur. Bu durumda küçük üçlü söz konusudur. Frekans oranı 6:5’tir. İki oran arasındaki fark küçük görünse de, bu küçük fark müziğin neşeli mi yoksa hüzünlü mü algılanacağını belirler. Armoninin temeli, işte bu iki basit sayısal ilişkiye dayanır.
Majör üçlü akor
Majör ve minör dizilerin tam sayı oranlarıyla kurulabildiğini artık biliyoruz. Bu bilgiden yola çıkarak bir adım daha atabiliriz. Aynı anda üç oranı bir araya getirdiğimizde, majör üçlü akor oluşur.
Bu üç ses rastgele seçilmez. İlk ses temel sestir; ikinci ses, temel sesten biraz daha tizdir; üçüncü ses ise en tiz olandır. Bu üç ses birlikte çalındığında, “majör akor” dediğimiz yapı ortaya çıkar.
Üç sesin frekansları basit bir matematiksel ilişki içindedir. En pes sesi 4 olarak kabul edersek, ortadaki ses 5, en tiz ses ise 6 olur. Yani oran 4:5:6’dır. Batı müziğinde majör akorun bu kadar merkezi olmasının nedeni, işte bu yalın ve dengeli matematiksel yapıdır.
Sonuç Olarak
Bir dahaki sefere klasik, rock, caz, opera ya da çağdaş müzik dinlediğinizde ya da çaldığınızda, matematik ile müziğin ortak yönlerini düşünün. Keyif aldığınız müziğin, matematiksel ilişkiler kullanılarak nasıl kurulduğunu fark etmeye çalışın.
Kaynak ve ileri okumalar:
- Maths in a minute: Maths and music; yayınlanma tarihi: 2 Kasım 2021.Kaynak site: Plus Math. Bağlantı: Maths in a minute: Maths and music;/
- Azaryahu, Libby & Ariel, Ido & Leikin, Roza. (2024). Interplay between music and mathematics in the eyes of the beholder: focusing on differing types of expertise. Humanities and Social Sciences Communications. 11. 10.1057/s41599-024-03631-z.
Matematiksel





