Matematikte mutlu ve mutsuz sayıları keşfetmek kolaydır. Örneğin 1 sayısı en mutlu sayılar arasında yer alır. Ancak 4 mutsuz bir sayıdır. Üstelik her ikisi de narsistik sayıdır. Peki ama tüm bunlar ne anlama gelir?

Sayılar hayatımızda birçok farklı biçimde karşımıza çıkar. Okul yıllarından hatırlayabileceğiniz gibi doğal sayılar, rasyonel ve irrasyonel sayılar, hatta sanal sayılar gibi farklı kümeler bulunur. Ancak bugün, bunların yerine daha eğlenceli bir kavrama odaklanacağız: mutlu sayılar.
Evet, mutlu sayılar matematikte gerçekten de vardır ve her ne kadar gerçek dünyada doğrudan bir uygulamaları bulunmasa da, ilginç ve şaşırtıcı özelliklere sahiptirler. Bu yüzden amatör matematikçiler arasında oldukça popülerdir.
Aslında tüm doğal sayılar, “mutlu” veya “mutsuz” olmak üzere iki kategoriye ayrılır. Hatta bu mutluluk kavramı daha da genelleştirilerek, kendilerine yoğun bir şekilde odaklanan “narsisistik sayılar” gibi özel sayı kümelerine de yol açar.
Mutlu Sayılar Ve Mutsuz Sayılar Hayatımıza Nasıl Girdi?

Mutlu sayılar kavramının ilk kez kimin tarafından geliştirildiği tam olarak bilinmemektedir. Ancak1960’larda İngiliz matematikçi Reginald Allenby tarafından popüler hale getirildiği kabul edilmektedir. Mutlu sayıları bulmak oldukça basittir. Bunun için herhangi bir doğal sayıyı alıp, rakamlarının karelerini hesaplayarak bu kareleri toplamanız yeterlidir. Örneğin, 13 sayısını ele alalım:
- Rakamlarının karelerini alalım: 1² = 1, 3² = 9
- Elde edilen kareleri toplayalım: 1 + 9 = 10
- Aynı işlemi 10 için tekrarlayalım: 1² + 0² = 1. Sonuç 1 olduğu için, 13 mutlu bir sayıdır.
Bu kavramın kim tarafından adlandırıldığı bilinmese de, sonsuz sayıda mutlu sayı olduğu sezgisel olarak anlaşılabilir. Ancak işin ilginç yanı, gerçek dünyada olduğu gibi, mutluluğa ulaşmaya çalışırken mutsuzlukla da karşılaşabilirsiniz. Örneğin, 4 sayısını alalım ve aynı işlemi uygulayalım:
- 4² = 16
- 1² + 6² = 1 + 36 = 37
- 3² + 7² = 9 + 49 = 58
- 5² + 8² = 25 + 64 = 89
- 8² + 9² = 64 + 81 = 145
- 1² + 4² + 5² = 1 + 16 + 25 = 42
- 4² + 2² = 16 + 4 = 20
- 2² + 0² = 4
Bu noktada döngü başa dönerek tekrar eder: 4 → 16 → 37 → 58 → 89 → 145 → 42 → 20 → 4. Eğer bir sayı bu döngüye girerse, asla 1’e ulaşamaz ve mutsuz bir sayı olarak adlandırılır. Mutlu sayılar kadar matematiksel olarak ilginç olan bu mutsuz sayılar, sayı teorisi içinde ilginç yapılar oluşturur ve matematik meraklıları arasında popüler bir çalışma alanı olmaya devam etmektedir.
Mutlu Ve Mutsuz Sayılar İçin Bir Genelleme Yapmak Mümkün müdür?
Küçük sayılar için bir sayının mutlu olup olmadığını hesaplamak mümkün olsa da, sayı büyüdükçe bu işlemi elle yapmak zorlaşır. Neyse ki, matematikçiler bunun için çeşitli algoritmalar geliştirmiştir
Matematikçiler ayrıca mutlu sayıların dağılımını ve yoğunluğunu da araştırmıştır. Yoğunluk (ρ), mutlu sayıların tüm doğal sayılara oranı olarak tanımlanır ve bu değer küçük sayılarda daha yüksekken, büyük sayılarda azalma eğilimi gösterir. Örnek olarak:
- İlk 10 doğal sayı içinde 3 mutlu sayı bulunur (ρ = 0,3).
- İlk 100 doğal sayı içinde 20 mutlu sayı vardır (ρ = 0,2).
- İlk 1000 doğal sayı içinde 143 mutlu sayı bulunur (ρ = 0,143).
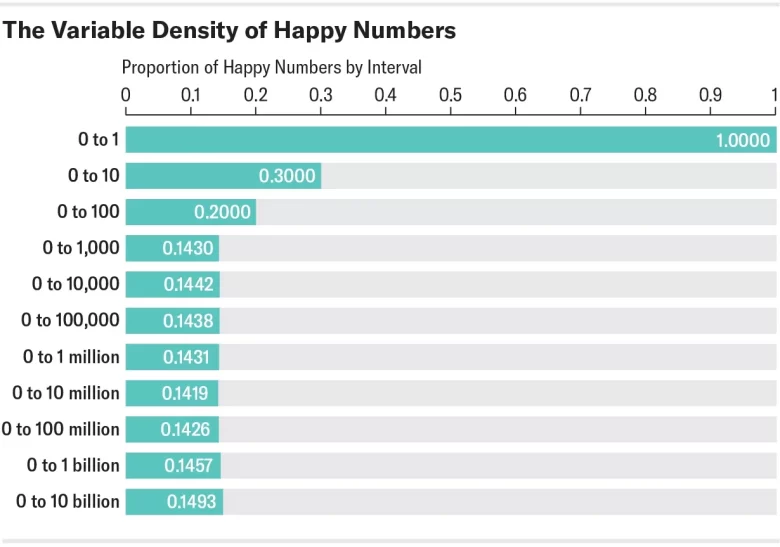
Yukarıdaki verilere bakıldığında, mutlu sayıların yoğunluğu yaklaşık %14 civarında sabitleniyor gibi görünebilir. Ancak, matematikçi Justin Gilmer, 2011 yılında mutlu sayıların sabit bir yoğunluğa sahip olmadığını ve yoğunluklarının incelenen sayı aralığına bağlı olarak değiştiğini kanıtladı. Yani mutlu sayıların büyüklükleri arttıkça belirli bir sınıra yaklaşmadıkları ortaya çıktı.
Ardışık Mutlu Sayılar Kaç Tanedir?
Matematikçileri meşgul eden bir diğer ilginç soru ise birbirini takip eden kaç tane mutlu sayının bulunabileceğidir. İlk iki ardışık mutlu sayı 31 ve 32’dir. Ancak üç ardışık mutlu sayı bulabilmek için dört basamaklı sayılara geçmek gerekir: 1.880, 1.881, 1.882.
2006 yılında matematikçi Hao Pan, herhangi bir sayıda ardışık mutlu sayının bulunabileceğini kanıtladı. Ancak bu tür dizileri bulmak için çok büyük sayılara gitmek gerekir:
- Dört ardışık mutlu sayı: 7.839 ile başlar.
- Beş ardışık mutlu sayı: 44.488 ile başlar.
- Altı ardışık mutlu sayı: 7.899.999.999.999.959.999.999.996 ile başlar. Bu bulgular, ardışık mutlu sayılar için belirli bir sınır olmadığı, ancak büyük kümeler halinde ortaya çıkmalarının giderek zorlaştığını göstermektedir.
Başka bir ilginç soru ise, bir mutlu sayıyı 1’e ulaştırmak için kaç işlem yapılması gerektiğidir. Ne kadar az işlem gerekiyorsa, sayı o kadar mutlu kabul edilecektir. 1, 10, 100 gibi sayılar doğrudan 1’e ulaştıkları için en mutlu sayılardır.13 gibi sayılar birkaç adımda 1’e ulaşır, ancak daha az mutludurlar.
Peki en az mutlu olan sayı hangisidir? İki basamaklı sayılar arasında 7’dir. 7’den 1’e gitmek için beş yineleme gerekir. Sırada 356 vardır ve bunun için altı hesaplama yapmanız lazım. Daha da az mutlu bir sayı istiyorsanız, 977 basamaklı bir sayı ile işe başlamanız gerekiyor. Dolayısıyla mutsuzluğun derecesinin bir sınırı yoktur.
Narsistik Sayılar Nedir?
Yukarıdaki satırlarda mutlu ve mutsuz sayılarla ilgili bazı çalışmalardan örnekler verdik. Ancak başta da belirttiğimiz gibi bir de narsistik sayılar vardır. Aslında bu sayılar, mutlu sayılar üzerine yapılan araştırmalar sırasında ortaya çıkan bir genellemenin sonucudur.

Bir doğal sayının her bir basamağındaki rakamın, sayının basamak sayısı kadar kuvveti alınıp toplandığında sayının kendisi elde ediliyorsa, bu tür sayılar narsistik sayı olarak adlandırılır.
- Örneğin, 243 sayısını ele alalım: 2³ + 4³ + 3³ = 8 + 64 + 27 = 99. Bu durumda 243 narsistik bir sayı değildir.
- Ancak 153 sayısı için aynı işlemi yaparsak: 1³ + 5³ + 3³ = 1 + 125 + 27 = 153. Bu tür sayılar narsistik sayı olarak kabul edilir.
Tek basamaklı sayıların tümü narsisttir. Ancak genel olarak yalnızca 89 tane narsistik sayı vardır. Bunlardan bazıları:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 153, 370, 371, 407, 1.634, 8.208, 9.474, 54.748, 92.727, 93.084, 548.834… ve en büyüğü 115.132.219.018.763.992.565.095.597.973.971.522.401’dir.
Matematikçiler, 60’tan fazla basamağa sahip narsistik sayıların olamayacağını kanıtlamışlardır. Yalnızca sonlu sayıda narsistik sayı olduğu için, mutlu sayılara kıyasla bu alanda daha az açık matematiksel soru bulunmaktadır. Ancak matematikçilerin “mutluluk” arayışı hiçbir zaman sona ermez.
Kaynak ve ileri okumalar
All Natural Numbers Are Either Happy or Sad. Some Are Narcissistic, Too. Yayınlanma tarihi: 24 Ekim 2023. Kaynak: Scientificamerican. Bağlantı: All Natural Numbers Are Either Happy or Sad. Some Are Narcissistic, Too
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel








