Alman matematikçi Martin Eichler’in “Matematikte 5 temel işlem vardır.” dediği rivayet edilir. Bunlar toplama, çıkarma, çarpma, bölme ve modüler formlardır.

Endişelenmeyin, modüler formlar matematik müfredatına beşinci bir temel işlem olarak eklenmiş değil. Aslında Eichler bu sözüyle modüler formların matematikte ve doğa bilimlerinde ne denli önemli olduğunu anlatmaktadır. Peki nedir bu modüler formlar?
Modüler formlar oldukça karmaşık ve tuhaf fonksiyonlardır. Genellikle son derece ayrıntılı simetrileri tanımlayan fonksiyonlar olarak karşımıza çıkmaktadır. Bu nedenle modüler formların ne olduğunu anlamak için simetriler üzerine konuşmakta fayda vardır.
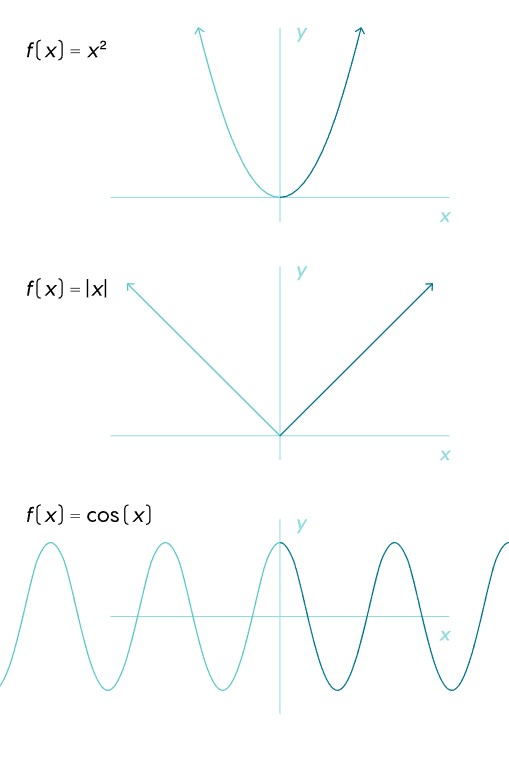
Matematik derslerinden hatırlayacağınız simetri, matematiksel bir nesnenin değişmeden kalmasını sağlayan dönüşümlerdir. Genelde 3 tür simetriden söz ederiz: Öteleme simetrisi, dönme simetrisi ve yansıma simetrisi. Simetrinin bu tanımına bakarak bir fonksiyonun da simetriye sahip olabileceğini kolaylıkla çıkarsayabilirsiniz. Örneğin y=x2 denklemi ile tanımlanan parabol, y eksenine göre simetriktir.
Bu ve bunun gibi birçok fonksiyonun simetriye sahip olduğunu söyleyebiliriz. Mesela trigonometrik fonksiyonlar da simetriye sahiptir. Bunun için kosinüs fonksiyonunu ele alabiliriz, kendini tekrar eden bir yapıya sahiptir. İşte modüler formlar da bu yönüyle trigonometrik fonksiyonlara benzemektedir. Ancak elbette trigonometrik fonksiyonlardan da son derece farklıdır. Gelin, işin biraz daha detayına inelim.
Karmaşık Sayılı Fonksiyonlardan Modüler Formlara
Yukarıda simetri kavramı üzerinden modüler formların simetri özelliğine sahip fonksiyonlarla benzerliğinden bahsettik. Artık yavaş yavaş modüler formları tanımaya başlayabiliriz. Ancak bunun için karmaşık sayılı fonksiyonlardan bahsetmemiz gerekecek.
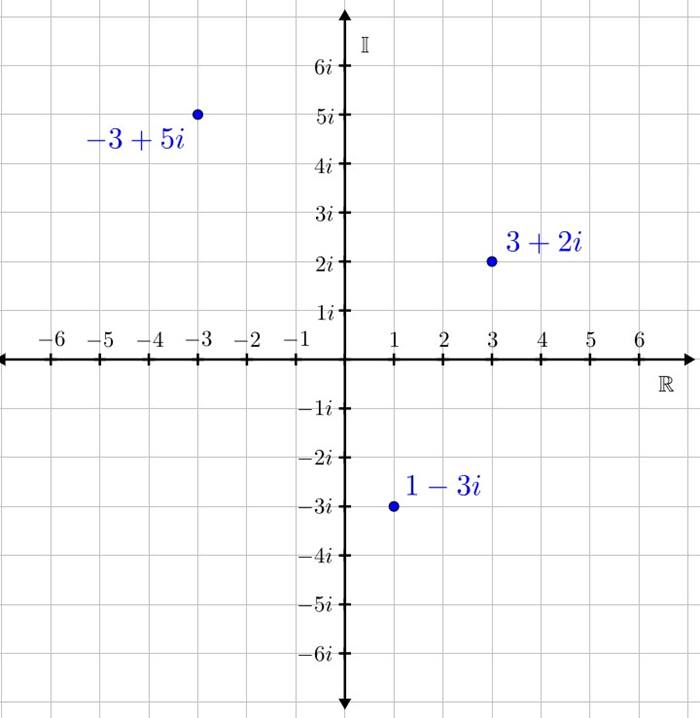
Karmaşık sayılar, temelde iki bileşenden oluşur: gerçel kısım ve imajiner kısım. Örneğin 1+i ifadesinde gerçel kısım 1, imajiner (sanal) kısım ise i’dir. Karmaşık sayıların bu ikili dünyası sayesinde herhangi bir iki boyutlu düzlemde bir nokta olarak temsil edilebilirdir.
Ancak karmaşık sayıları görselleştirmesi o kadar kolay değildir. Bu nedenle matematikçiler genelde renklendirmeye başvururlar. Mesela bunu karmaşık düzlemi renklendirerek yaparlar. Ancak burada karmaşık sayıların kartezyen koordinatlarını değil, polar (kutupsal) koordinatları kullanırlar.
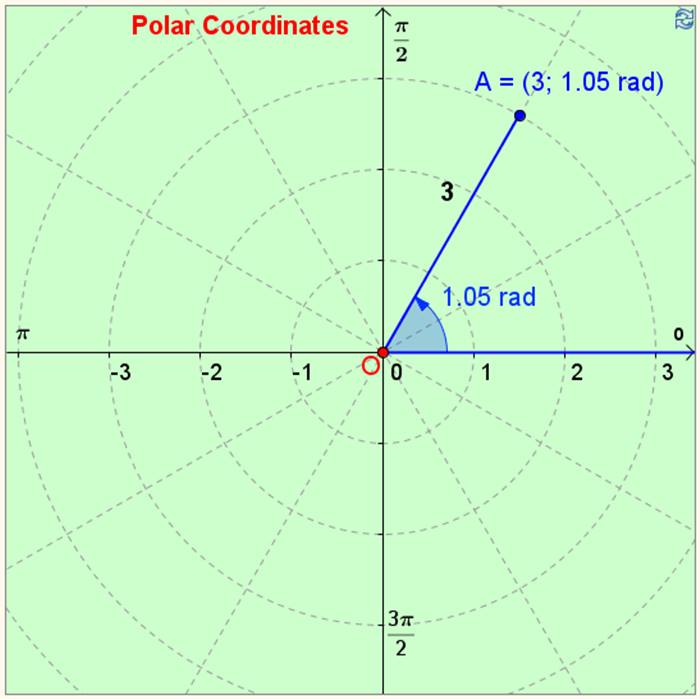
Tıpkı yukarıdaki görselde olduğu gibi kutupsal koordinat sistemindeki her noktanın karşılık geldiği açı bir renkle renklendirilir. Örneğin merkezin sağında noktaların 0 derecelik açı yaptığı (yani x ekseni üzerine denk gelen yerde) yerler kırmızıdır. Açının büyümesiyle renkler de değişecektir.
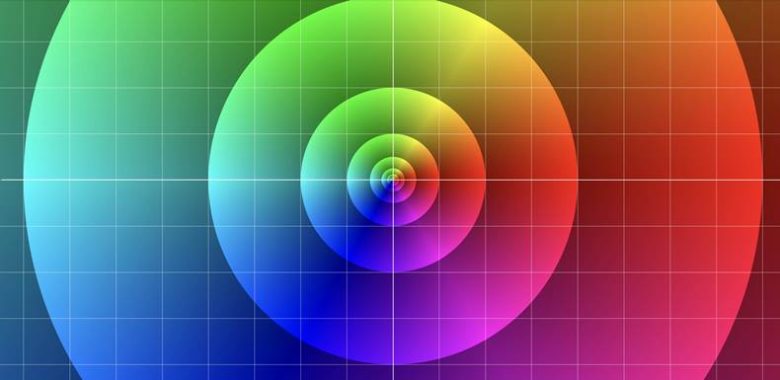
O halde yukarıdaki görseldeki f(z)=z fonksiyonundan yararlanarak daha karmaşık fonksiyonların da görselleştirmesini yapabiliriz. Örneğin f(z)=z2 ‘yi deneyelim. z karmaşık sayısını da 1+i olarak kabul edelim. 1+i karmaşık sayısının karesi 2i edecektir. Yukarıdaki görseldeki renklendirme örüntüsünü kullanacak olursak grafiğimiz şu şekilde görünecektir:

Peki Tüm Bu Simetriler ve Renkler Ne İşe Yarıyor?
Buraya kadar konuyu daha kolay anlayabilmek adına simetri özelliğinden ve bu özellik altında modüler formların nasıl görüneceğinden bahsettik. “İyi hoş ama bunların amacı ne” diye düşünmüş olabilirsiniz. İşte bu noktada modüler formlar diye bir şeye neden ve nasıl ihtiyacımız olduğuna, yani modüler formların ortaya çıkışına değinmek yararlı olacaktır.
1920 ve 30’larda Alman matematikçi Erich Hecke, modüler formlar üzerine çalışmış en önemli isimlerin başında geliyordu. Onun geliştirdiği teori, 20 ve 21. yüzyıl matematiğinin büyük bir kısmına yön vermiştir. Bu durumu daha iyi anlamak adına gelin şu soruyu birlikte düşünelim.
Verilen bir tamsayıyı dört karenin toplamı olarak kaç farklı şekilde yazabilirsiniz? Örneğin 0’ı dört karenin toplamı olarak yalnızca 1 şekilde yazabilirsiniz. Ancak 1’i 8, 2’yi 24 ve 3’ü 32 şekilde yazabilirsiniz. İşte 1, 8, 24, 32 şeklinde ilerleyen bu diziyi matematikçiler şu şekilde ifade ettiler:
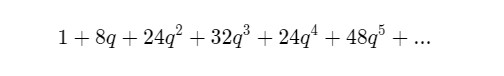
Denklemin katsayılarına baktığımızda kolay yakalanabilecek bir örüntünün olmadığını fark ediyoruz. Bu nedenle matematikçiler de örneğin q174 ‘ün katsayının ne olması gerektiğini bulamıyordu. Fakat modüler formların önceki bölümlerde bahsettiğimiz özellikleri bu noktada çok işe yarıyordu. Modüler formlar yardımıyla her katsayı için bir formül elde edebiliyoruz.
Çünkü modüler formlar, sahip olduğu güzel simetri ve oluşturduğu renkli görüntüyle güzel görünmekle kalmıyor. Aynı zamanda bu özellikleri onu son derece kısıtlayıcı kılıyor. Ve tekrar eden simetriler, matematiksel nesneler arasında uyumun bir formülünü çıkarmak için birebirdir.
Modüler Formlar Nerelerde Karşımıza Çıkıyor?
Modüler formların 20 ve 21. yüzyıl matematiğine büyük katkıları olduğundan bahsetmiştik. Ve her geçen gün bu katkının arttığını söyleyebiliriz. Öyle ki 2022 Fields madalyasını küre paketleme problemini çözerek kazanan Maryna Viazovska‘nın çözümünde de modüler formlara rastlarız.

Ayrıca modüler formlar, sicim teorisi ve kuantum fiziğindeki parçacık etkileşimlerinin potansiyel modellerini incelememize de olanak sağlamaktadır. Fakat modüler formları bu kadar meşhur eden en önemli şey, Fermat’nın Son Teoremi‘dir. Çünkü Fermat’nın Son Teoremi’nin 1994 yılındaki kanıtı modüler formlara dayanmaktadır.
Fermat’nın Son Teoremi’ni kanıtlayan Andrew Wiles, kanıtı için öncelikle eliptik eğri oluşturmak için kullanılan varsayılan çözümden yararlanmıştı. Daha sonra böyle bir eğriye her zaman benzersiz bir modüler form atfedilebileceğini göstermişti. Fakat bu durumda bir çelişki oluşuyordu. İşte bu çelişki sayesinde Andrew Wiles, varsaydığı çözümün doğru olmadığına ulaşmıştı.
Wiles’ın başarısı sadece bir asırlık sorunu çözmekle kalmamıştı. Kriptografi ve hata düzeltme kodlarında önemli bir rol oynayan eliptik eğrilerin de daha iyi anlaşılmasını sağlamıştı. Bunun yanı sıra ispat, sayılar teorisi ve geometri arasındaki bağlantıyı da güçlendirmişti. Bu bağlantının güçlenmesi ise günümüzde Langlands Programı adı verilen bir çalışma alanının doğmasına yol açtı.
Dolayısıyla rahatlıkla diyebiliriz ki, bu ve bunun gibi birçok makalede, çalışma alanında modüler formlarla karşılaşırsanız şaşırmayın.
Kaynaklar ve İleri Okumalar
- Behold Modular Forms, the ‘Fifth Fundamental Operation’ of Math ; Bağlantı: Behold Modular Forms, the ‘Fifth Fundamental Operation’ of Math. Kaynak site: Quanta Magazine ; Yayınlanma tarihi: 21 Eylül 2023
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel






