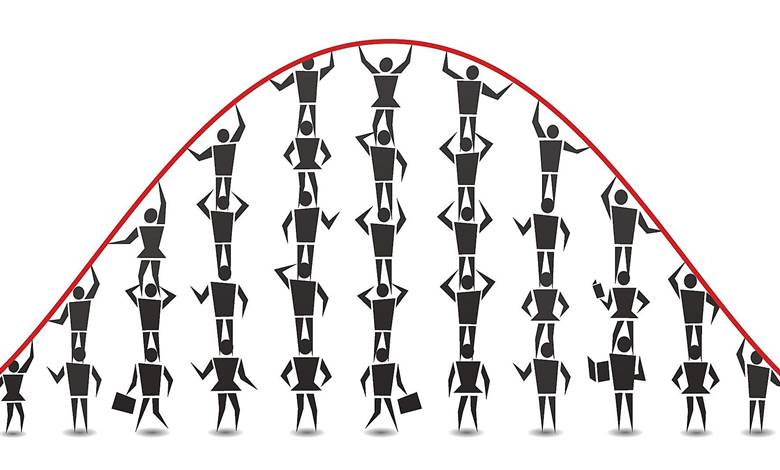
Matematikteki en çarpıcı kurallardan biri olan Merkezi Limit Teoremi bize çok sayıda rasgele bağımsız olayları topladığımızda çıkan sonucun normal eğri tarafından yaklaşık değerinin bulunabileceğini söyler.
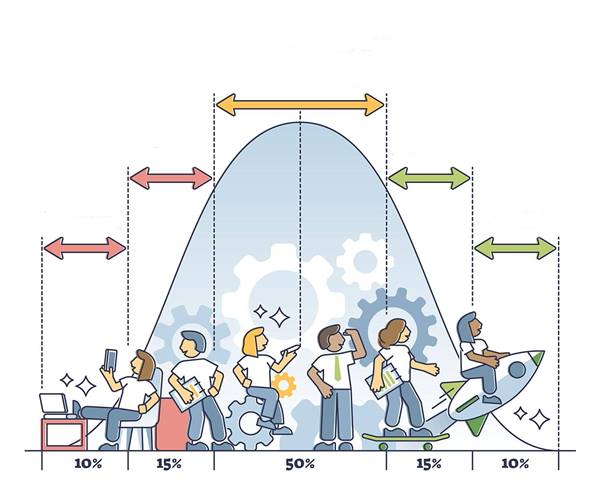
İstatistikteki ana fikir, küçük bir örneğe bakarak bütün bir popülasyon hakkında bir şeyler söyleyebilmenizdir. Bu fikir olmasaydı, kamuoyu yoklamaları veya seçim tahminleri olmazdı. Yeni tıbbi ilaçları veya köprülerin güvenliği gibi şeyleri test etmenizin bir yolu da olmazdı. Bütün bunları merkezi limit teoremi sayesinde yapabiliyoruz.
Tanıma geçmeden önce basit bir örnek verelim. Diyelim ki İstanbul’da yaşayan kişilerin ortalama kilosunu hesaplamak istediniz. Bunu nasıl yapacaksınız? Her kişinin tek tek kilosunu ölçme ve sonra da ortalamasını almanız mümkün olmadığına göre daha kestirme bir yol kullanmanız gerekecektir.
Eğer bir miktar istatistik biliyorsanız, aklınıza rastgele seçtiğiniz 100 kişinin ağırlığını ölçmek ve sonrasında da bu grubun ortalamasını hesaplamak gelecektir. Ancak burada da bir sorun bulunmaktadır. Sonuçta elde edeceğiniz bu sayının size İstanbul’da yaşayan herkes hakkında bir fikir vermesi gerekiyor.
Ama bu ortalamanın içine dahil ettiğiniz kişilerin bunu yansıttığından emin misiniz? Belki de çok zayıf ya da fazla kilolu kişileri seçmişsinizdir. Bu nedenle, elinizdeki ortalamanızın, geneli ne kadar temsil ettiğine dair bir fikir sahibi olmak için, seçtiğiniz 100 kişinin ortalama ağırlığının popülasyona göre nasıl değiştiği hakkında bir şeyler bilmeniz gerekir.
Bunu başka 100 kişilik gruplar alıp, sonra da bu grupların ortalama ağırlığını hesaplayıp ve nihayetinde elde ettiğiniz tüm sonuçların birbiri ile uyumlu olup olmadığını kontrol ederek yapabilirsiniz. Ancak elinizdeki ortalamaların ortalaması olarak elde ettiğiniz rakam şu an size ne demektir?
Merkezi Limit Teoremi Nedir?
Merkezi limit teoremine göre, verilerin gerçek dağılımına bakılmaksızın, örneklem büyüklüğü arttıkça, bir veri örneğinin ortalaması, söz konusu genel popülasyonun ortalamasına daha yakın olacaktır. Genel olarak doğru bir tahmin elde edebilmeniz için 30-50 arasında 100 kişilik grupları tartıp, ortalamalarını almanız yeterli olacaktır.
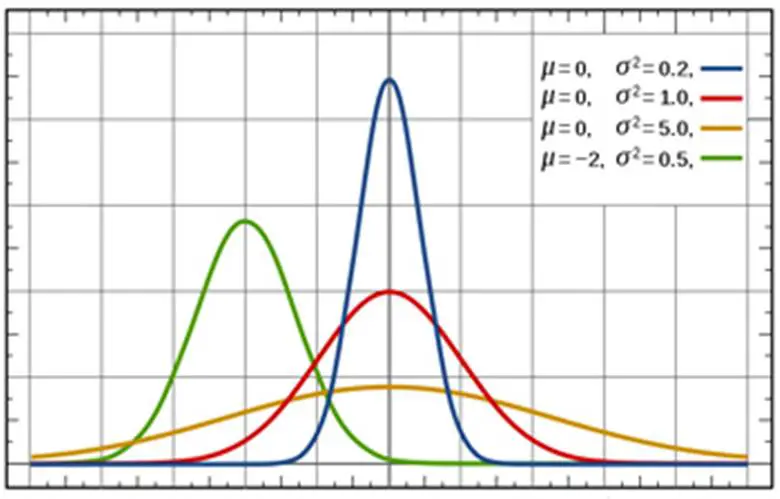
Ne kadar çok örnek alınırsa, grafiğe döktüğünüz zaman ortaya çıkan sonuç normal dağılım şeklini alır. Normal dağılım dediğimiz zamanlarda da bir çoğumuzun adını duyduğu çan eğrisi gelmelidir. Normal dağılımın en göze çarpan özelliklerinden biri şekli ve mükemmel simetrisidir.
Böyle bir grafiği tam olarak ortadan katlarsanız, her biri diğerinin ayna görüntüsü olan iki eşit yarım elde edersiniz. Ve bu normal dağılımın ortalaması, popülasyondaki gerçek ortalama ağırlığa eşit olduğundan, gözlemlenen ortalamanız, gerçek ortalamanın iyi bir tahminidir.
Merkezi Limit Teoremi Neden Önemlidir?
Merkezi limit teoremi genellikle, örneklem ortalamalarının ve standart sapmaların ortalamasının, örneklem boyutu büyüdükçe popülasyon ortalamasına ve standart sapmaya eşit olmaya yaklaşacağını belirten büyük sayılar yasasıyla birlikte kullanılır. Bu, popülasyonların özelliklerini doğru bir şekilde tahmin etmek son derece yararlıdır. ( İstatistik Bilgilerini Yanlış Yorumlamanın 7 Büyük Günahı ve Bunlardan Kaçınma Yolları)
Bu kavram ilk olarak 1733’te Abraham de Moivre tarafından geliştirilmiş olmasına rağmen, 1930’da ünlü Macar matematikçi George Pólya’nın onu merkezi limit teoremi olarak adlandırmasına kadar resmi olarak kullanılmamıştır.
İstatistiksel tahmin elde etme sanatına kesinlik kazandıran merkezi limit teoremidir ve aynı zamanda normal dağılımın her yerde karşımıza çıkmasının da arkasındaki sebeptir. Ancak merkezi limit teoremi aslında burada açıkladığımızdan biraz daha matematiksel bir dil taşır.
Merkezi limit teoreminin kendi formülü yoktur, ancak hesaplamalar örnek ortalamasına ve standart sapmaya dayanır. Bu hesaplamaların nasıl yapıldığını merak ederseniz buraya da bakabilirsiniz.
Kaynaklar ve ileri okumalar:
- Central Limit Theorem (CLT); yayınlanma tarihi: 28 Haziran 2022; Bağlantı: https://www.investopedia.com/
- Maths in a minute: The central limit theorem; Kaynak site: Plus Math. Yayınlanma tarihi: 19 Nisan 2016; Bağlantı: Maths in a minute: The central limit theorem;/
- Maths in a minute: The normal distribution; Kaynak site: Plus Math. Yayınlanma tarihi: 7 Ocak 2022; Bağlantı: Maths in a minute: The normal distribution
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel