Günlük dilde “limit” kelimesi, bir miktarın, bir düşüncenin ya da herhangi bir şeyin ötesine geçilemeyen sınırlarını tanımlamak için kullanılır. Örneğin, hız limiti yasal olarak izin verilen maksimum hızı, kredi kartı limiti ise kullanılabilecek en yüksek bakiyeyi ifade eder.
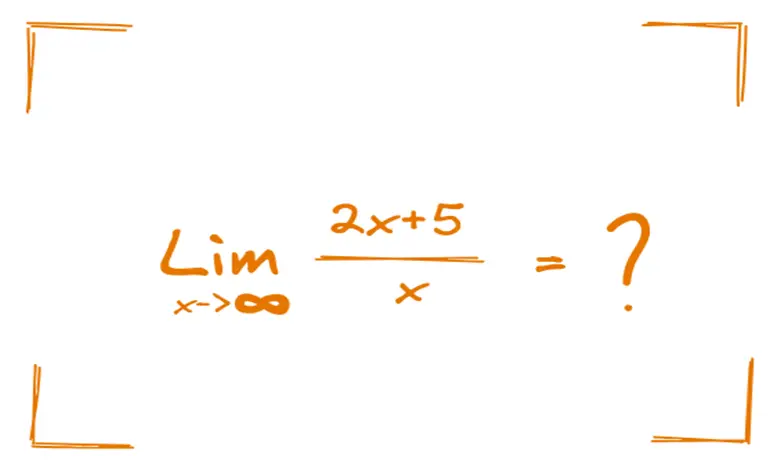
Bu iki örnek, “limit” kavramının üst sınır anlamındaki kullanımını yansıtır. Ancak “limit” alt sınırlar için de geçerlidir. Örneğin, bir kredi başvurusu için gerekli minimum kredi puanı da bir limit türüdür.
Matematikte limitten bahsedildiğinde ise, genellikle bir fonksiyonun belirli bir noktadaki davranışı kastedilir. Yani, x değerleri belirli bir sayıya yaklaşırken, fonksiyonun grafiğinin nasıl bir eğilim gösterdiği incelenir. Bu kavramı daha net anlayabilmeniz için, şimdi bir örnekle açıklayalım.
Limit Nedir?

Bir kek düşünün. Keki önce ikiye böldüğünüzü hayal edin. Sonra bu yarımları tekrar ikiye bölün. Ardından oluşan parçaları yine ikiye ayırın. Bu işlemin sonsuza kadar sürdüğünü düşünün. Parçaların boyutları hakkında ne söyleyebiliriz?
Parçaların her adımda küçüldüğünü rahatlıkla fark edersiniz. Bölmeye devam ettikçe bu parçalar bir saç telinden daha ince, hatta teoride bir atomdan bile küçük hale gelir. Yani bu parçaları istediğiniz kadar küçültmek mümkündür. Bu durum, bir dizinin bir sınıra yaklaşmasına sezgisel bir örnek oluşturur. Bu örnekte ortaya çıkan dizi şöyledir: 1, 1/2, 1/4, 1/8, 1/16, …
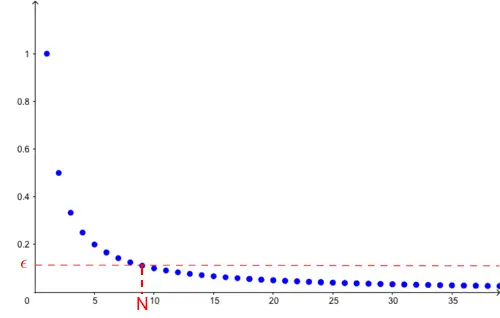
Bu dizideki sayılar keki bölmeye devam ettikçe elde edilen parçaların büyüklüğünü gösterir. Terimler giderek 0’a yaklaşır. Ne kadar küçük bir sayı seçerseniz seçin, dizinin bir noktasından sonra gelen tüm değerler o sayıdan daha küçüktür. Grafik de bu davranışı açık biçimde gösterir: yatay eksen dizide ilerlemeyi, düşey eksen ise o adımdaki değeri belirtir.
Bir dizinin sınırı her zaman 0 olmak zorunda değildir. Örneğin 3/2, 5/4, 9/8, 17/16, …dizisini ele alalım. Bu dizi, kek örneğindeki her terimin üzerine 1 eklenerek elde edilir. Bu durumda dizinin sınırı 1’dir, çünkü terimler adım adım 1’e yaklaşır. Yeterince ilerlediğinizde, dizideki sayılar 1’e istediğiniz kadar yakın olur.
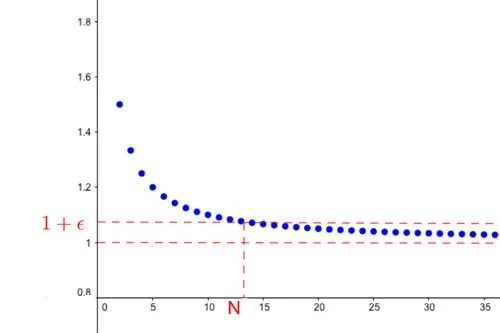
Genel matematik dilinde a0, a1, a2, a3,…gerçek sayılardan oluşan bir dizi olsun. Bu dizinin L sınırına yakınsadığı söylenir; çünkü 0’dan büyük her ε için öyle bir N vardır ki n>N olduğunda dizinin an değeri L’den ε kadar küçük bir uzaklık içinde kalır. Bu durum aşağıdaki gibi gösterilir.

Limit Ne İşe Yarar?
Günlük hayatta birine “Limit size ne kazandıracak?” diye sorulduğunda buna net bir cevap vermek kolay değildir. Hatta limitin doğrudan bir işinize yaramayacağını söylemek çok da yanlış sayılmaz. Fakat biraz daha geniş açıdan baktığınızda durum değişmeye başlar.
Değişmeyen tek şey dünyanın sürekli değiştiğidir. Türev ve integral, değişimi anlamanın matematiksel araçlarıdır. Değişimin olduğu her yerde bu iki kavram karşımıza çıkar. Türev ve integralin temelinde ise her zaman limit vardır. Bu nedenle, değişimi anlamaya ihtiyaç duyulan her durumda limit sessizce yerini alır.

Matematikte içinde limit kelimesi geçen bir başka teorem daha vardır. Ancak bunlar sadece isim benzerliğidir. Göz atmak isterseniz: Merkezi Limit Teoremi Nedir? Neden Önemlidir?
Kaynaklar ve ileri okumalar:
- Maths in a minute: Limits; yayınlanma tarihi: 22 Nisan 2022; Kaynak site: Plus Math. Bağlantı: Maths in a minute: Limits;
- Maths in five minutes: Calculus; yayınlanma tarihi: 22 Nisan 2022; Kaynak site: Plus Math. Bağlantı: Maths in five minutes: Calculus;
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel





