Yeni bir eve taşınırken karşılaşılan en büyük zorluklardan biri, mevcut mobilyaların yeni evin odalarına taşınmasıdır. Mobilyalar genellikle bir önceki evin boyutlarına ve düzenine göre seçildiğinden, yeni evin dar veya dönüşlü koridorlarından geçirme süreci tam bir mücadeleye dönüşecektir.

Özellikle koridor düz değil, keskin bir dönüşe sahipse, bu durum başlı başına bir sorun haline gelir. İşte bu günlük hayatta karşılaşılan problem, matematik dünyasında uzun yıllardır çözülmeye çalışılan bir bilmecenin, Taşınan Kanepe Probleminin ( İng: moving sofa problem) temelini oluşturur.
1950’li ve 1960’lı yılların en önde gelen matematikçilerinden biri olan Avusturya-Kanadalı Leo Moser (1921-1970), özellikle sayılar teorisi üzerine derinlemesine çalışmalar yapmış önemli bir isimdir. Moser, matematiksel problemlere olan yoğun ilgisi ve analitik yaklaşımıyla tanınırdı.

Leo Moser (1921-1970), matematiksel analiz, kombinatorik ve geometri alanlarında çalışmış Kanadalı bir matematikçidir. En çok Moser teoremi ve Moser sayıları ile tanınır.
Moser’in yenilikçi bakış açısı ve problem çözmeye yönelik tutkusu, Taşınan Kanepe Problemi gibi soyut ve eğlenceli matematiksel sorulara da ilgi duymasını sağladı. Mose bu problemi ölümünden 4 sene evvel geliştirdi. Ancak üzerinden 50 yıldan fazla zaman geçmesine rağmen kesin bir çözüme henüz ulaşılamadı.
Taşınan Kanepe Problemi, ilk bakışta eğlenceli ve soyut bir düşünce deneyi gibi görünecektir. Ancak aslında geometri ve optimizasyon alanında derin bir meydan okumayı temsil eder. Matematikçiler bu problemi çözmeye çalışırken, geometri, analiz ve optimizasyonun kesiştiği yeni ve beklenmedik sonuçlarla karşılaşırlar.
Taşınan Kanepe Yani Moving Sofa Problemi Nedir?

Öncelikle, gerçek dünyanın aksine bu problemi iki boyutlu bir perspektifte ele almak gerekiyor. Yani, mobilyayı yukarı kaldırma ya da döndürme gibi üçüncü boyuttaki manevralar bu problemde mümkün değil.
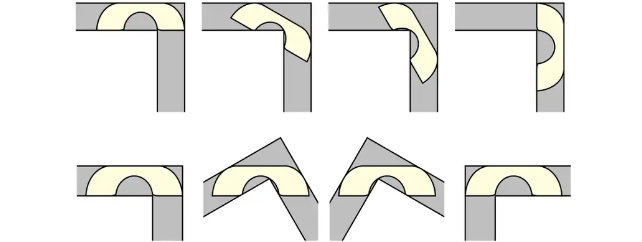
Düşünün ki taşınma esnasında dar bir koridora denk geldiniz ve koridor bir L şeklinde keskin bir dönüşe sahip. Taşımaya çalıştığınız mobilyanın bu köşeden dönüp dönmeyeceği tamamen şekline ve boyutlarına bağlı. Bu durumda, köşeden dönmesi mümkün olan en büyük mobilyanın alanını hesaplamak gibi bir soruyla karşı karşıyayız.

Taşınması gereken mobilyanın kenar uzunluğu 1 cm olan bir kare olduğunu varsayalım. Bu durumda, kare mobilyamızın alanı 1 cm² olacaktır. Koridorun L şeklindeki dönüşü, bu boyuttaki bir mobilya için oldukça basittir.

Akla gelecek bir sonraki şekil, yarım daire biçiminde bir kanepe olacaktır. Bu durumda kanepemizin yarıçapını 1 cm olarak kabul edersek alanı , π/2 (yani yaklaşık 1.57) olacaktır. Aşağıdaki görselde de gördüğünüz gibi bu şekildeki bir kanepeyi de köşeden döndürmek mümkün. Ancak bu şeklin en büyük alana sahip olduğundan emin miyiz?

Aslında değiliz. Matematiksel olarak, daha karmaşık bir şeklin daha büyük bir alanla köşeden dönmesi mümkün.. Taşınan Kanepe Problemi, tam olarak bu soruya yanıt arayan bir problemdir. Amacı, köşeden dönecek maksimum alanlı kanepeyi bulmaktır.
Yıllar İçinde Birbirinden İlginç Kanepeler Bulunmaya Başladı

1960’lardan bu yana matematikçiler, bu problemi çözmek için daha karmaşık geometrik şekiller tasarlamışlardır. 1990 yılında matematikçi John Hammersley, yarım daireyi iki çeyrek daireye böldü, aralarına bir dikdörtgen ekledi. Köşeden dönebilmesi içinde bu şeklin içinden bir başka yarım daire çıkardı. Elde edilen bu şeklin alanı 2/π+π/2 yani yaklaşık 2.2074 kadardı. Uzun zaman bu şeklin optimal çözüm olduğu düşünüldü.
Ancak 1992 yılında, Rutgers Üniversitesi’nden Joseph Gerver, Hammersley’in tasarımını aşan bir çözüm buldu. Karmaşık eğrilerden oluşan bir şekil, şu ana kadar köşeden dönebilecek en büyük kanepe alanını (yaklaşık 2.2195 cm²) temsil etmektedir. Gerver kanepesinin en büyük şekil olduğu düşünülse de, kesin olarak kabul etmemiz ya da etmememiz mümkün değil.
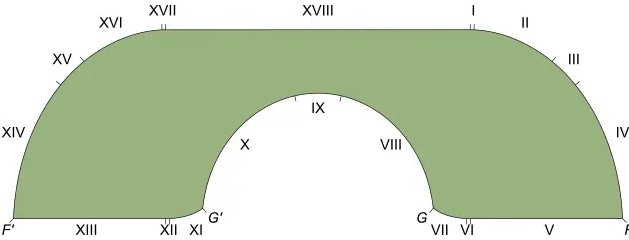
Taşınan Kanepe Problemi Çözülmüş Olabilir
Şu anda Güney Kore’deki Yonsei Üniversitesi’nde doktora sonrası araştırmacı olarak görev yapan Jineon Baek, Taşınan Kanepe Problemi’nin çözümüne nihayet ulaştığını düşünüyor. Baek, 2023 yılında yayımladığı 100 sayfalık kapsamlı çalışmasında, Gerver’in 1992’de bulduğu çözümün gerçekten optimal olduğunu kanıtlamayı amaçladı.
Baek’in çalışması, Gerver Kanepesi’nin yaklaşık 2.2195 birim karelik alanıyla bu problemin bilinen en büyük çözümünü temsil ettiğini matematiksel araçlarla doğruluyor. Çalışmada modern matematiksel yöntemler kullanılarak, Gerver Kanepesi’nin hareketli kanepe problemi için optimal şekil olduğu ve bu sınırın aşılamayacağı öne sürülüyor.
Kanıt, hem matematiksel doğruluk hem de çözümün kapsamlılığı açısından oldukça etkileyici ve Gerver’in şeklinin geçerliliğini güçlü bir şekilde destekliyor.
Sonuç olarak
Gerver Kanepesi, Hareketli Kanepe Problemi’nde şimdiye kadar yapılan en önemli katkılardan biri olmaya devam ediyor. Karmaşık yapısı ve büyük alanıyla, bu problemdeki ilerlemeyi sembolize ediyor. Matematik dünyası ise bu çözümün optimal olduğunu kesin olarak doğrulamak veya daha büyük bir çözüm bulmak için araştırmalarını sürdürüyor.
Baek’in çalışması, bu problemi çözme yolunda önemli bir adım olarak kabul edilse de, henüz bağımsız matematikçiler tarafından tam olarak doğrulanmamıştır. Çalışma, matematik camiasının detaylı incelemesine tabi olup, kesin kabul için daha fazla analiz gerektirmektedir.
Kaynaklar ve ileri okumalar:
- The Moving Sofa Problem. Numberphile; yayınlanma tarihi: 24 Mart 2017; Kaynak site: Numberphile; Bağlantı: The Moving Sofa Problem
- Kallus, Yoav and Dan Romik. “Improved upper bounds in the moving sofa problem.” Advances in Mathematics (2017): n. pag.
- This 100-Page Proof Claims to Have Solved the World’s. Most Frustrating Math Puzzle: What’s The Largest Sofa That Fits Around a Corner? Kaynak site: ZME Science. Yayınlanma tarihi: 12 Aralım 2024. Bağlantı: This 100-Page Proof Claims to Have Solved the. World’s Most Frustrating Math Puzzle: What’s The Largest Sofa That Fits Around a Corner?
- Why Mathematicians Cannot Solve the Problem of Moving Your Sofa. Yayınlanma tarihi: 24 Mart 2017; Kaynak site: Popular Mechanics. Bağlantı: Why Mathematicians Cannot Solve the Problem of Moving Your Sofa/
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel





